Cosenos directores. Cálculo vectorial.

Introducción

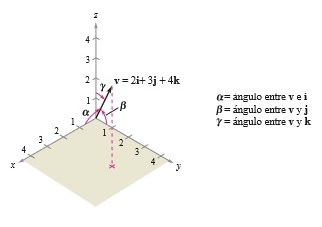
En el espacio es conveniente medir la dirección en términos de los ángulos entre el vector v distinto de cero y los tres vectores unitarios i, j, k, como se muestra en la figura 1. Los ángulos $\alpha$ , $\beta$ y $\gamma$ son los ángulos de dirección de v, y $\cos{\alpha}$ , $\cos{\beta}$ y $\cos{\gamma}$ son los cosenos directores de v. Como

$\bold{v} \cdot \bold{i} = ||\bold{v}|| ||\bold{i}|| \cos{\alpha} = ||\bold{v}|| \cos{\alpha}$

Figura 1. Cosenos directores. *Nodo Universitario de la Universidad de Guanajuato, Introducción a la geometría analítica del espacio. [Figura]. Recuperado de:* https://oa.ugto.mx

$\bold{v} \cdot \bold{i} = (v_1, v_2, v_3) \cdot (1,0,0) = v_1$

se sigue que $\displaystyle \cos{\alpha} = \frac{v_1}{||\bold{v}||}$ . Mediante un razonamiento similar con los vectores unitarios $\bold{j}$ y $\bold{k}$ , se tiene

$\displaystyle \cos{\beta} = \frac{v_2}{||\bold{v}||}$

$\displaystyle \cos{\gamma} = \frac{v_3}{||\bold{v}||}$

Entonces

\displaystyle \cos{\alpha} = \frac{v_1}{||\bold{v}||}

\displaystyle \cos{\beta} = \frac{v_2}{||\bold{v}||}

Por consiguiente, cualquier vector $\bold{v}$ distinto de cero en el espacio tiene la forma normalizada

$\displaystyle \frac{\bold{v}}{||\bold{v}||} = \frac{v_1}{||\bold{v}||} \bold{i} + \frac{v_2}{||\bold{v}||} \bold{j} + \frac{v_3}{||\bold{v}||} \bold{k}$

$\displaystyle \frac{\bold{v}}{||\bold{v}||} = \cos{\alpha} \bold{i} + \cos{\beta} \bold{j} + \bold{\gamma} \bold{k}$

y como $\displaystyle \frac{\bold{v}}{||\bold{v}||}$ es un vector unitario, se sigue que

$\cos^2{\alpha} + \cos^2{\beta} + \cos^2{\gamma}=1$

Problema resuelto

Problema. Hallar los cosenos y los ángulos directores del vector $\bold{v} = 2 \bold{i} + 3\bold{j} + 4 \bold{k}$ , y mostrar que $\cos^2{\alpha} + \cos^2{\beta} + \cos^2{\gamma}=1$ .