Movimiento rectilíneo uniforme. Física.

Introducción

El movimiento rectilíneo uniforme de efectúa en línea recta (una sola dimensión). Comprende el desplazamiento y tiempo que originan la velocidad, la cual permanece constante y se calcula mediante la razón $v=d/t$ . Generalmente, lo que mide es la velocidad media ( $v_{media}$ ), que representa un promedio y se calcula mediante valores conocidos a diferentes tiempos; en este caso, los valores inicial y final.

Figura 1. Representación del movimiento rectilíneo uniforme.

La ecuación para determinar la velocidad instantánea es

$\displaystyle v = \frac{\Delta d}{\Delta t}$

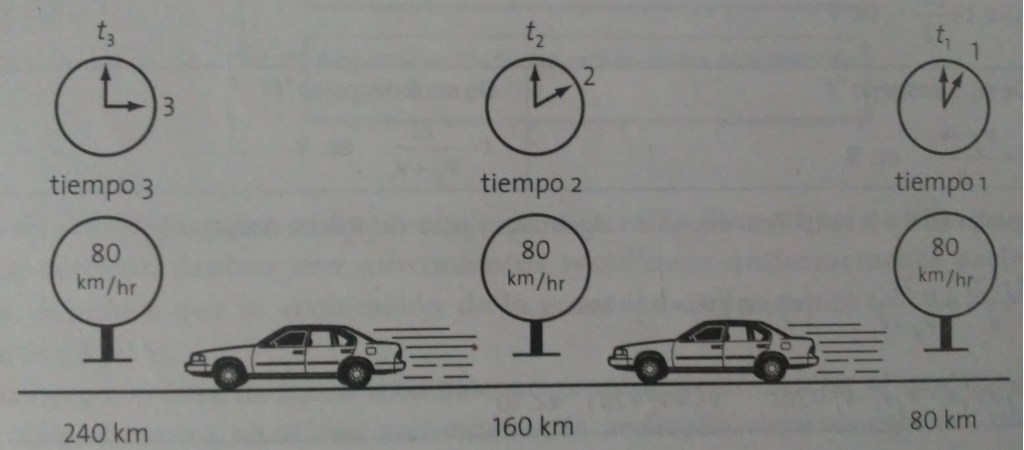
Si un cuerpo se desplaza con velocidad constante y por una trayectoria rectilínea, se dice que se trata de un movimiento rectilíneo uniforme.

La ecuación para determinar la velocidad es la siguiente

$\displaystyle v = \frac{d}{t}$

donde:

$v$ es la velocidad, en m/s (metros por segundo).
$d$ es la distancia recorrida, en m (metros).
$t$ es el tiempo en que se recorre la distancia, en s (segundos).

Problemas resueltos

Problema 1. En un viaje en automóvil de una ciudad a otra, una parte del camino se realiza por carretera libre y otro por autopista, en el primer tramo se recorren 55 km en 30 min y en el segundo 15 km en 15 min. Determinar la velocidad promedio del viaje.

Solución. Utilizando la fórmula de la velocidad

$\displaystyle \overline{v} = \frac{55 \ km + 15 \ km}{30 \ min + 15 \ min}$

$\displaystyle \overline{v} = \frac{70 \ km}{45 \ min}$

$\displaystyle \therefore \overline{v} = 1.556 \ (km/min)$

Expresando el resultado en metros por segundo

$\displaystyle \overline{v} = 1.556 \ (km/min) \left(\frac{1 \ min}{60 \ s} \right) \left(\frac{1000 \ m}{1 \ km} \right)$

$\displaystyle \therefore \overline{v} = 25.93 \ (m/s)$

Problema 2. Una unidad deportiva está ubicada a 5 km de distancia de la casa de Adrián y tarda 15 minutos en trasladarse hasta allí. ¿A qué velocidad promedio viaja Adrián?

Solución. Se tienen los siguientes datos

$d = 5 \ km$
$v = 15 \ min$

Primero se debe realizar la conversión de kilómetros a metros (unidades del SI)

$\displaystyle d = 5 \ km = 5 \ km \left( \frac{1000 \ m}{1 \ km} \right) = 5 000 \ m$

y de minutos a segundos

$\displaystyle t = 15 \ min = 15 \ min \left( \frac{60 \ s}{1 \ min} \right) = 900 \ s$

Utilizando la fórmula

$\displaystyle v = \frac{d}{t}$

$\displaystyle v = \frac{5000 \ m}{900 \ s}$

$\displaystyle v = 5.55 \ (m/s)$

Si se desea expresarlo en km/h, se tiene lo siguiente

$\displaystyle v = 5.55 \ (m/s) = 5.55 \ (m/s) \left( \frac{1 \ km}{1000 \ m} \right) \left( \frac{60 \ s}{1 \ min} \right)$

$\displaystyle \therefore v = 20 \ (km/h)$

Problema 3. Una persona que vive en la ciudad de México viaja a la ciudad de Veracruz en autobús, el cual mantiene la velocidad límite de 95 km/h durante todo el trayecto y tarda 4 horas y 20 minutos en llegar. ¿Qué distancia hay entre México y Veracruz?

Solución. Se tiene los datos