Introducción
La aceleración se presenta cuando ocurre un cambio de velocidad con respecto al tiempo. Se define como la variación de la velocidad en la unidad de tiempo.
se caracteriza por que depende tanto de los cambios de magnitud como de dirección de los velocidad. Cuando la aceleración permanece constante, se trata de un movimiento rectilíneo uniformemente acelerado (MRUA). Las demás ecuaciones que lo describen se deducen a partir de estas ecuaciones básicas.
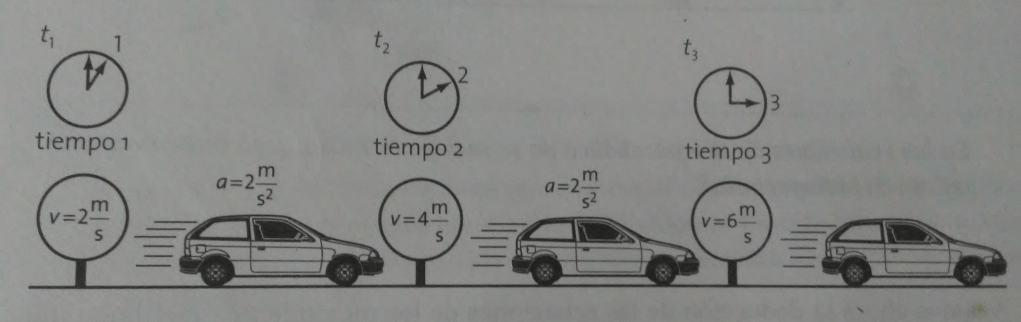
Figura 1. Representando el MRUA.
Fórmulas del movimiento rectilíneo uniformemente acelerado
La fórmula de la aceleración contiene variables que se pueden calcular despejándose de esta ecuación, dependiendo de los datos con que se cuente. Si se despeja la velocidad final como sigue, se tiene que
Al involucrar la velocidad media, se observa que
Sustituyendo en la primera ecuación
Por último, utilizando nuevamente la fórmula de la velocidad media y el despeje de la fórmula de la aceleración, se muestra que
Continuando
Las ecuaciones obtenidas del movimiento rectilíneo uniformemente acelerado se muestran a continuación.
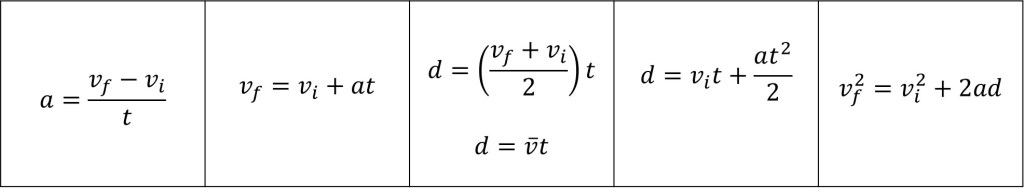
En el estudio de cualquier movimiento es importante conocer que dirección se considera positiva:
- para el desplazamiento, será positivo si está por encima del punto de partida, y será negativo si está por debajo del punto de partida.
- para la velocidad, será positiva si el movimiento es a favor de la dirección elegida como positiva mientras que es negativa si el movimiento está en contra de la dirección elegida como positiva.
- para la aceleración, será positiva si la fuerza está a favor de la dirección elegida como positiva pero se será negativa es porque va en contra de la dirección elegida como positiva.
Problemas resueltos
Problema 1. ¿Cuál es la aceleración de una motocicleta que pasa del reposo a 140 km/h en 10 s?
Solución. Se tienen los siguientes datos
Tomando la fórmula de la ecuación de la aceleración y sustituyendo
El resultado está expresado en km/h s debido a que las motociclistas pueden cambiar de velocidad en espacios de tiempo muy cortos.
Problema 2. Cuando un patinador que parte del reposo desciende por una rampa alcanza una aceleración de 3 , durante 5 segundos. Determinar su rapidez final.
Solución. Se tienen los siguientes datos
Tomando la siguiente fórmula
Sustituyendo
La velocidad final del patinador es de 15 m/s.
Problema 3. Un camión que lleva una carga de grava viaja en una carretera a una velocidad constante de 70 km/h. De pronto frena. El tramo que tardó en detenerse quedó marcado en el pavimento con las huellas de las llantas en una superficie de 40 m. ¿Cuál fue la aceleración media durante el frenado? ¿Cuánto tiempo tardó en detenerse?
Solución. Se tienen los siguientes datos
Primero, se realiza la conversión de km/h a m/s de la velocidad inicial.
Después, se calcula la aceleración despejando la siguiente fórmula
La aceleración es negativa porque el camión va frenando. Por último, de la fórmula de la aceleración, se despeja la variable .
La aceleración media durante el frenado fue de 4.72 y el tiempo que transcurrió hasta detenerse fue 4.11 segundos.