Aceleración centrípeta. Física.

Introducción

Independiente de que el movimiento sea circular uniforme o circular variado, siempre está presente la aceleración centrípeta o radial ( $a_c$ ), que es la causa de que la velocidad tangencial, localizada en la periferia de la circunferencia, cambie permanentemente de dirección y sentido, pero no influye en su valor. Esta aceleración siempre es perpendicular a la velocidad tangencial, por lo que tiende hacia el centro, de ahí el término de centrípeta.

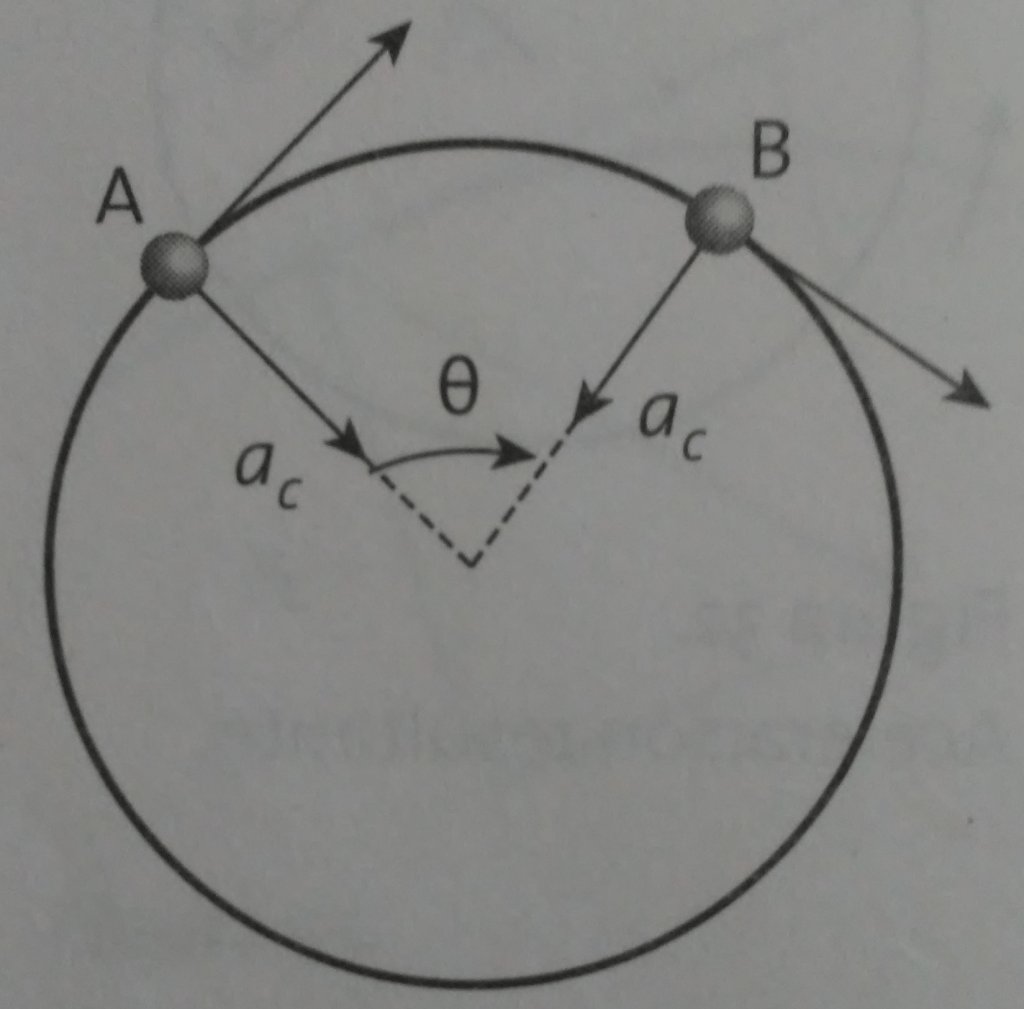
Figura 1. Representación gráfica de la aceleración centrípeta.

Relación entre la aceleración centrípeta, velocidad angular y velocidad tangencial.

Figura 2. Deducción de la aceleración centrípeta.

La relación entre aceleración centrípeta, velocidad tangencial y velocidad angular se obtiene seleccionando dos puntos de la trayectoria circular. Posteriormente, se calcula la diferencial de vectores tangenciales $\Delta v = v_{t_2} - v_{t_1}$ por método gráfico, lo cual implica cambiar el sentido de $v_{t_1}$ . Pero como ambos tienen la misma magnitud, sólo se utiliza el símbolo $v_t$ , y aplicando a los triángulos formados las propiedades de semejanza, se cumple que

$\displaystyle \frac{\Delta v}{v_t} = \frac{s}{r}$

pero $\displaystyle v_t = \frac{s}{t}$ , así que al despejar $s$ de esta última y sustituir en la primera se tiene

$\displaystyle \frac{\Delta v}{v_t} = \frac{v_t \ t}{r}$

Reacomodando

$\displaystyle \frac{\Delta v}{t} = \frac{v_t^2}{r}$

Al primer cociente se le llama aceleración centrípeta, $a_c$ ; por tanto,

$\displaystyle a_c = \frac{v_t^2}{r}$

donde:

$a_c$ es la aceleración centrípeta, en $m/s^2$ .
$v_t$ es la velocidad tangencial o lineal, en $m/s$ .
$r$ es el radio, en $m$ .

Y como $v_t = \omega \ r$ , se sustituye en la última ecuación para obtener también

$\displaystyle a_c = \frac{(\omega \ r)^2}{r}$

$\displaystyle a_c = \omega ^2 \ r$

donde

$a_c$ es la aceleración centrípeta, en $m/s^2$ .
$\omega$ es la velocidad angular, en $rad/s$ .
$r$ es el radio, en $m$ .

Si el movimiento es circular variado se presentan simultáneamente la aceleración tangencial ( $a_t$ ) y la centrípeta ( $a_c$ ).

Figura 3. Representación gráfica de la aceleración resultante.

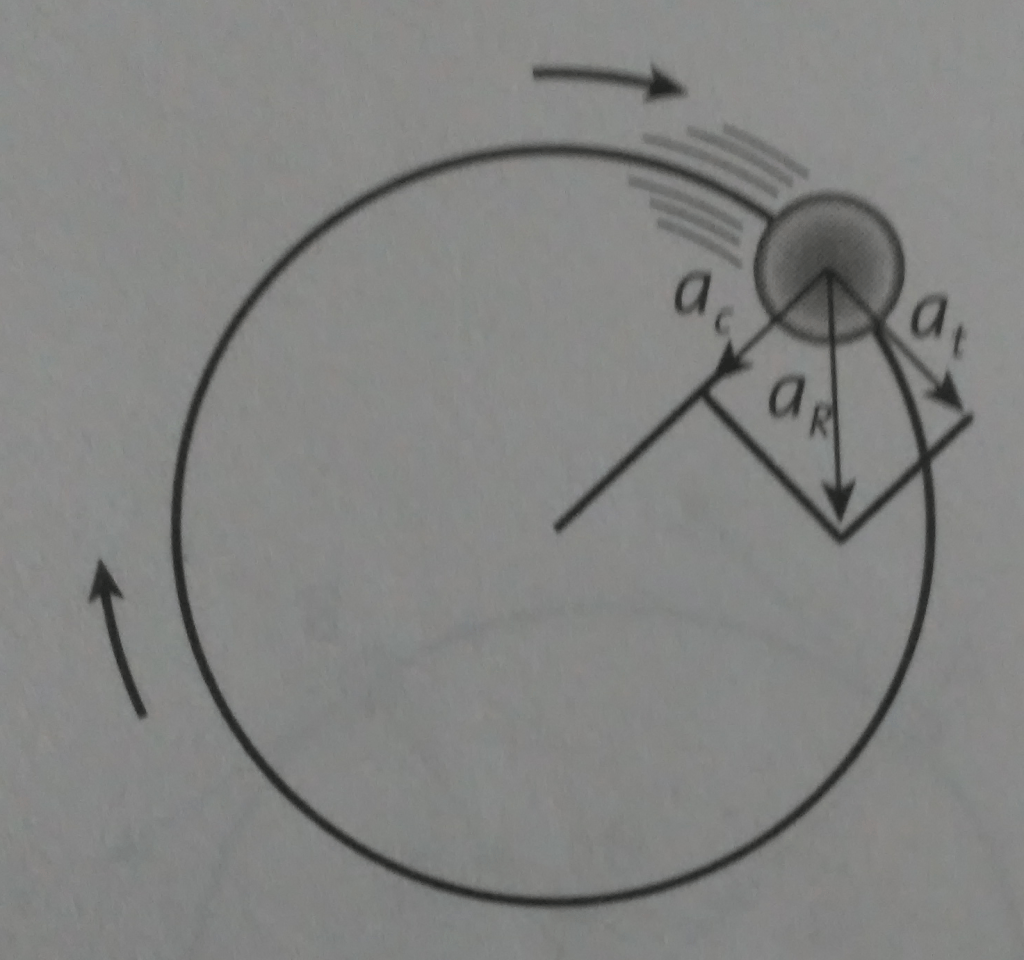
Un ejemplo es el automóvil de carreras que entra en una curva acelerando o frenando o el lanzamiento de un disco. Cuando se requiera calcular la aceleración resultante ( $a_R$ ), se deben sumar vectorialmente ambas aceleraciones.