Sea C una curva en el plano y sea L una recta no paralela a ese plano. al conjunto de todas las rectas paralelas a L que cortan a C se le llama cilindro. A C se le llama la curva generadora (o la directriz) del cilindro y a las rectas paralelas se les llama rectas generatrices.

Figura 1. Cilindro circular recto.

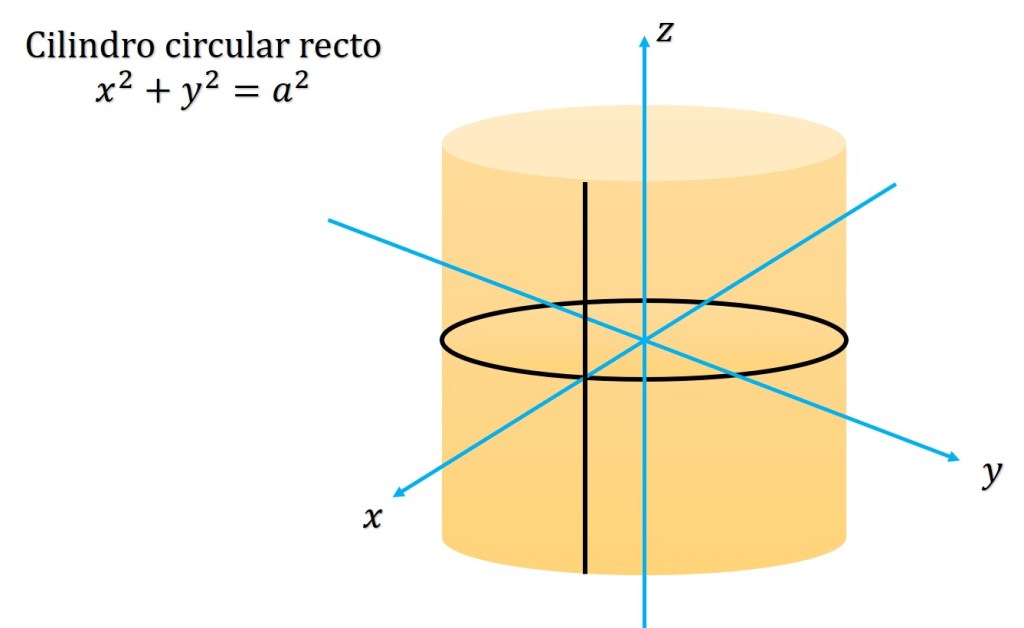
La ecuación de la (curva) directriz del cilindro recto mostrado en la figura 1 es

x^2 + y^2 = a^2

Esta es la ecuación en plano xy.

Para encontrar una ecuación del cilindro, hay que observar que se puede generar cualquiera de las (rectas) generatrices fijando los valores de x y y dejando que z tome todos los valores reales. Es decir, la ecuación del cilindro es la ecuación de su curva generadora o directriz.

x^2+y^2=a^2

La ecuación de un cilindro cuyas rectas generatrices son paralelas a uno de los ejes coordenados contiene sólo las variables correspondientes a los otros dos ejes.

Problema resuelto

Problema. Trazar la superficie representada por cada una de las ecuaciones

  • a) z=y^2
  • b) z=\sin{x}, 0 \le x \le 2\pi

Solución (a). La gráfica es un cilindro cuya directriz, z=y^2, es una parábola en el plano yz. Las generatrices del cilindro son paralelas al eje x, como se observa en la figura 2.

Figura 2.

Solución (b). La gráfica es un cilindro generado por la curva del seno en el plano xz. Las generatrices son paralelas al eje y, como se observa en la figura 3.

Figura 3.
Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.