Problemas de movimiento circular. Física.

Problema 1. Al realizar un movimiento circular acelerado, un objeto describe un radio de 0.25 (m) y efectúa una vuelta completa en 0.41 (s). Para este instante, calcular:

a) Velocidad angular
b) Velocidad tangencial
c) Aceleración tangencial
d) Aceleración centrípeta
e) Aceleración resultante

Figura 1. Análisis del objeto en movimiento circular acelerado.

Solución. Los datos que se tiene son $T = 0.41 \ (s)$ , $r=0.25 \ (m)$ y $t=0.41 \ (s)$ .

Solución a). Al efectuar una vuelta completa el cuerpo presenta una velocidad angular de

$\displaystyle \omega = \frac{2\pi}{T}$

$\displaystyle \omega = \frac{2\pi}{0.41 \ s}$

$\displaystyle \therefore \omega = 15.325 \ (rad/s)$

Solución b). La velocidad que tiene el cuerpo en la periferia de la circunferencia descrita al dar una vuelta completa es

$\displaystyle v_t = \frac{2\pi \ r}{T}$

$\displaystyle v_t = \frac{2\pi (0.25 \ m)}{0.41 \ s}$

$\displaystyle \therefore v_t = 3.831 \ (m/s)$

En caso de romperse el hilo que lo sujeta, sería el valor de la velocidad con la cual escaparía de manera tangencial al movimiento descrito.

Solución c). El valor de la aceleración angular que tiene al dar una vuelta completa es

$\displaystyle \alpha = \frac{\omega}{t}$

$\displaystyle \alpha = \frac{15.325 \ (rad/s)}{0.41 \ (s)}$

$\alpha = 37.378 \ (rad/s^2)$

El valor que representa la aceleración en la periferia del movimiento circular que tiene el mismo sentido que la velocidad tangencial y es consecuencia de que esta última varíe es

$a_t = \alpha \ r$

$a_t = (37.378 \ rad/s^2)(0.25 \ m)$

$\therefore a_t = 9.345 \ (m/s^2)$

Solución d). El cantidad que causa que la velocidad tangencial cambie continuamente de dirección y sentido es

$\displaystyle a_c = \frac{v_t^2}{r}$

$\displaystyle a_c = \frac{(3.831 \ m/s)^2}{0.25 \ m}$

$\displaystyle \therefore a_c = 58.706 \ (m/s^2)$

Solución e). El vector de la aceleración resultante consiste en sumar dos vectores, el primero es la aceleración centrípeta con sentido siempre hacia el centro y el segundo es la aceleración tangencial siempre tangente a la periferia de la circunferencia descrita. Entonces,

$\displaystyle a_R = \sqrt{a_c^2 + a_t^2}$

$\displaystyle a_R = \sqrt{(58.706 \ m/s^2)^2 + (9.345 \ m/s^2)^2}$

$\displaystyle a_R = 59.445 \ (m/s^2)$

Figura 2. Representando la pieza metálica que está sujeta a una cuerda.

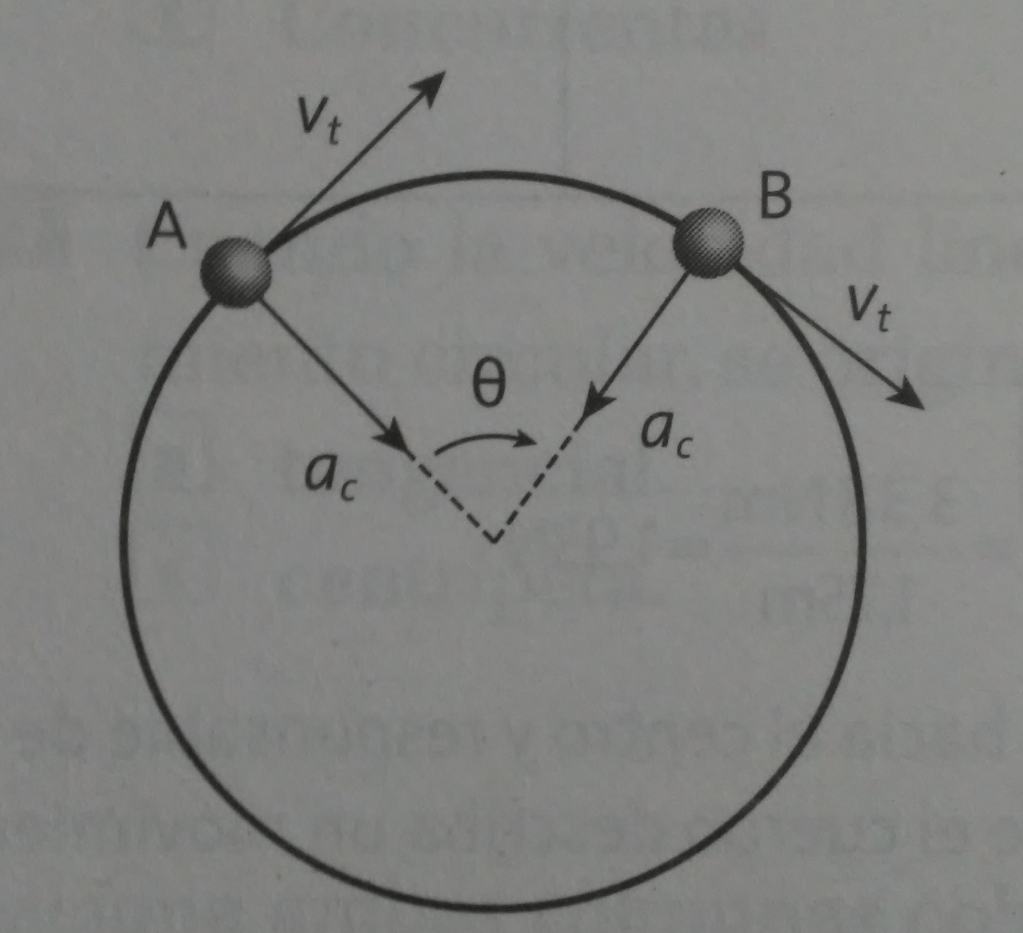
Problema 2. Una pieza metálica sujeta a una cuerda describe un movimiento circular con radio de 0.29 (m) y tarda 0.25 (s) en dar una vuelta completa. ¿Qué aceleración centrípeta presenta?

Solución. Los datos que se tienen son $r=0.29 \ (m)$ y $T = 0.25 \ (s)$ .

Solución a). El tiempo dado es el periodo, ya que es el tiempo necesario para efectuar una vuelta completa. El valor de la velocidad en la periferia con la cual gira, y que al variar de magnitud origina una aceleración tangencial característica del movimiento circular acelerado es

$\displaystyle v_t = \frac{2\pi r}{T}$

$\displaystyle v_t = \frac{2\pi (0.29 \ m)}{0.25 \ s}$

$\displaystyle v_t = 7.289 \ (m/s)$

La magnitud del vector que hace que la velocidad tangencial en la periferia de la trayectoria circular cambie permanentemente de dirección y sentido es

$\displaystyle a_c = \frac{v_t^2}{r}$

$\displaystyle a_c = \frac{(7.289 \ m/s)^2}{0.29 \ m}$

$\displaystyle \therefore a_c = 183.205 \ (m/s^2)$

Problema 3. Un objeto metálico de 0.04 (kg) de masa se hace girar mediante una cuerda de 1.75 (m) de longitud. Si ésta presenta en su superficie una velocidad tangencial de 9.2 (m/s), ¿cuál es su fuerza centrípeta?

Figura 3. Representando un objeto metálico atado a una cuerda.

Solución. Los datos que se tienen son $m=0.04 \ (kg)$ , $r=1.75 \ (m)$ y $v_t = 9.2 \ (m/s)$ .

Tomando la fórmula de la fuerza centrípeta

$\displaystyle F_c = \frac{M v_t^2}{r}$

$\displaystyle F_c = \frac{(0.04 \ kg)(9.2 \ m/s)^2}{1.75 \ m}$

$\displaystyle \therefore F_c = 1.935 \ (N)$

Este es el valor de la fuerza con que la cuerda sujeta al cuerpo hacia el centro y responsable de que se origine la aceleración centrípeta que hace que el cuerpo describa un movimiento circular.

Problemas de movimiento circular. Física.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Problemas de movimiento circular. Física.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta