Superficies de revolución. Cálculo vectorial.

Introducción

Se considera la gráfica de la función

$\displaystyle y = r(z)$

en el plano $yz$ (curva generadora o directriz). Si esta gráfica se gira sobre el eje $z$ , forma una superficie de revolución (figura 1). La traza de la superficie en el plano $z=z_0$ en un círculo cuyo radio es $r(z_0)$ y su ecuación es

$\displaystyle x^2+y^2={[r(z_0)]}^2$

Al sustituir $z_0$ por $z$ se obtiene una ecuación que es válida para todos los valores de $z$ . De manera similar, se pueden obtener ecuaciones de superficies de revolución para los otros dos ejes.

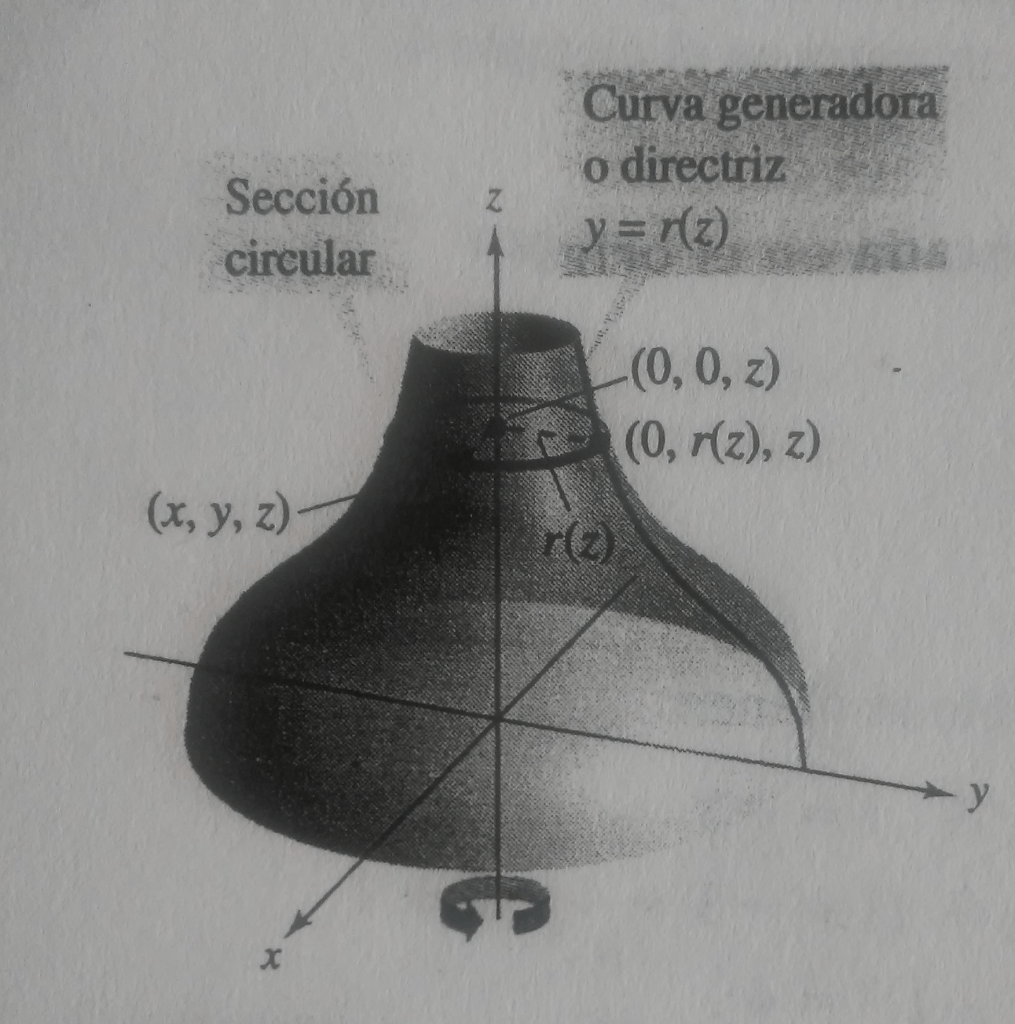
Figura 1. Superficie de revolución que gira sobre el eje z.

En general, si la gráfica de una función radio $r$ se gira sobre uno de los ejes coordenados, la ecuación de la superficie de revolución resultante tiene una de las formas siguientes

Girada sobre el eje $x$ : $\displaystyle y^2+z^2={[r(x)]}^2$
Girada sobre el eje $y$ : $\displaystyle x^2+z^2={[r(y)]}^2$
Girada sobre el eje $z$ : $\displaystyle x^2+y^2={[r(z)]}^2$

Problemas resueltos

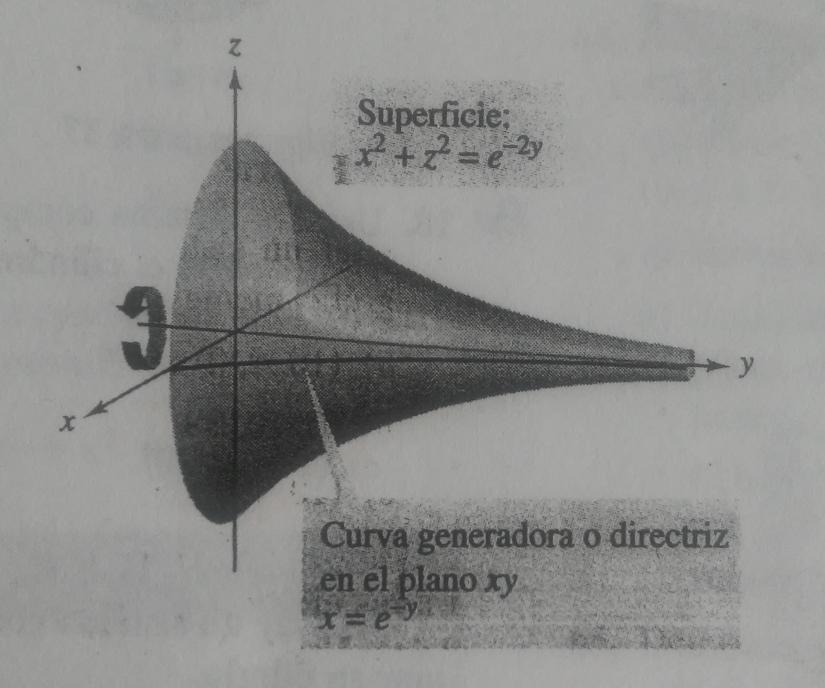
Problema 1. Hallar la ecuación de la superficie de la función $\displaystyle y=\frac{1}{z}$ en torno al eje $x$ y dibujarla.

Solución. La función radio es

$\displaystyle y = \frac{1}{z}$

Tomando la ecuación que gira en torno al eje $z$ y sustituyendo se tiene

$\displaystyle x^2 + y^2 = {r(z)}^2$

$\displaystyle x^2 + y^2 = {\left(\frac{1}{z} \right)}^2$

$\displaystyle \therefore x^2 + y^2 = \frac{1}{z^2}$

Graficando la función, se tiene lo siguiente

Problema 2. Encontrar una ecuación para la superficie generada al girar la gráfica $9x^2=y^3$ en torno al eje $y$ .

Solución. Se despeja $x$ para que la función se exprese en términos de $y$ (debido a que la gráfica gira en torno al eje $y$ ).

$\displaystyle 9x^2=y^3$

$\displaystyle x^2=\frac{y^3}{9}$

$\displaystyle x=\sqrt{\frac{y^3}{9}}$

$\displaystyle x=\frac{y^{3/2}}{3} = r(y)$

Ahora, la ecuación para esta superficie es

$\displaystyle x^2+z^2={[r(y)]}^2$

$\displaystyle x^2+z^2={\left(\frac{y^{3/2}}{3} \right)}^2$

$\displaystyle \therefore x^2+z^2=\frac{y^{3}}{9}$

La gráfica para esta ecuación es la siguiente

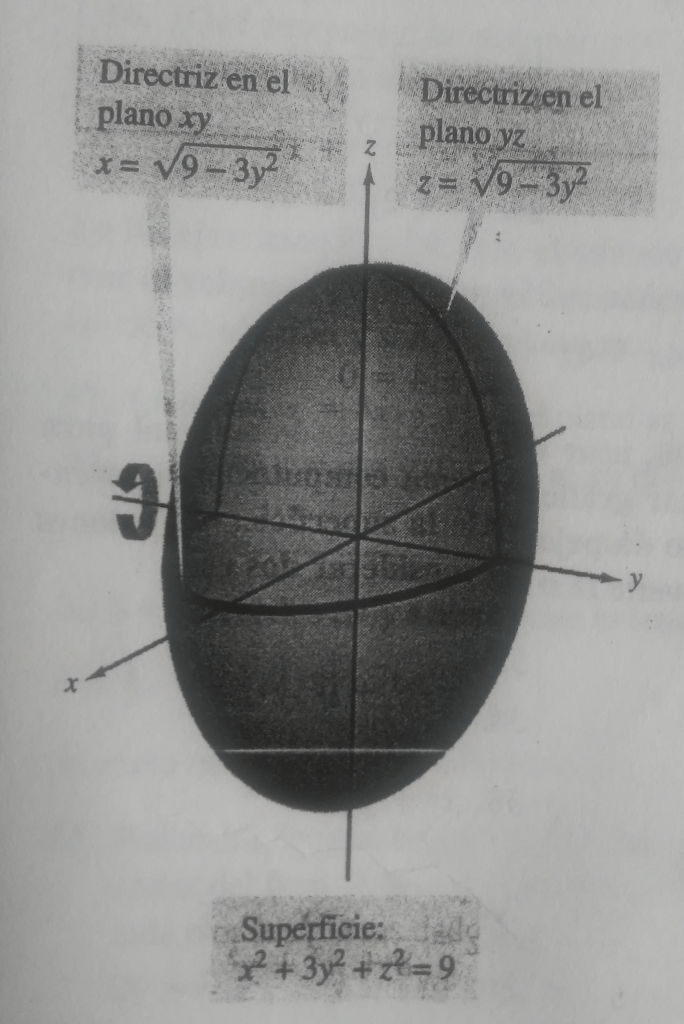
Problema 3. Hallar una directriz y el eje de revolución de la superficie dada por $x^2+3y^2+z^2=9$ .

Solución. La ecuación tiene una de las formas siguientes

Girada sobre el eje $x$ : $\displaystyle y^2+z^2={[r(x)]}^2$
Girada sobre el eje $y$ : $\displaystyle x^2+z^2={[r(y)]}^2$
Girada sobre el eje $z$ : $\displaystyle x^2+y^2={[r(z)]}^2$

Analizando la ecuación, se observa que los coeficientes $x^2$ y $z^2$ son iguales, por lo que se elige la tercera forma. Entonces, despejando la ecuación de la superficie

$\displaystyle x^2+3y^2+z^2=9$

$\displaystyle x^2+z^2=9-3y^2$

Se observa que

Por lo que la superficie tiene al eje $y$ como su eje de revolución. Ahora, se puede elegir una directriz de las trazas siguientes

Traza en el plano $xy$ : $\displaystyle x^2=9-3y^2$
Traza en el plano $yz$ : $\displaystyle z^2=9-3y^2$

Al usar la primera traza, la directriz es la semielipse dada por

$\displaystyle x = \sqrt{9-3y^2}$

Y usando la segunda traza, la directriz es otra semielipse dada por

$\displaystyle z = \sqrt{9-3y^2}$

Finalmente, la gráfica de esta superficie se muestra en la figura 4.

Por ultimo…

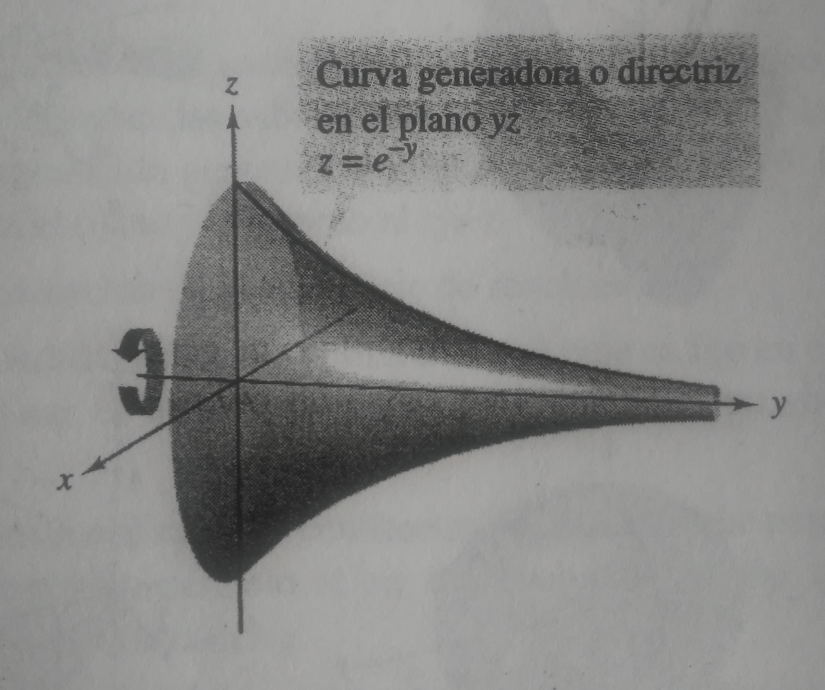
La curva generadora o directriz de una superficie de revolución no es única. Por ejemplo, la superficie $\displaystyle x^2 + z^2 = e^{-2y}$ puede generarse al girar la gráfica de $x=e^{-y}$ en torno al eje $y$ o la gráfica de $z=e^{-y}$ sobre el eje $y$ (figura 5).