La diferencial. Cálculo integral.

Introducción

Para la función $y=f(x)$ , se define que

$dx$ , llamada la diferencial de $x$ , dada por la relación $dx=\Delta x$ .
$dy$ , llamada la diferencial de $y$ , dada por la relación $dy= f'(x) \Delta x$ .

La diferencial de la variable independiente es, por definición, el incremento de la variable. Pero la diferencial de la variable dependiente no es igual a su incremento.

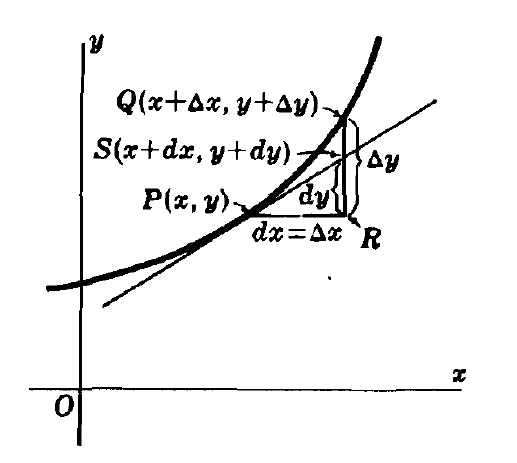
Figura 1. Representando la función con incrementos

La diferencial $dy$ puede hallarse mediante la definición $dy=f'(x) \ dx$ o por medio de reglas de derivación. Por ejemplo

$\displaystyle \frac{d}{dx}(c)=0 \quad \rightarrow \quad d(c) =0$

$\displaystyle \frac{d}{dx}(x)=1 \quad \rightarrow \quad d(x) = dx$

$\displaystyle \frac{d}{dx}(cu)=c \frac{du}{dx} \quad \rightarrow \quad d(cu) = c \ du$

$\displaystyle \frac{d}{dx}(e^u)= e^u \frac{du}{dx} \quad \rightarrow \quad d(e^u) = e^u \ du$

$\displaystyle \frac{d}{dx} \left(\frac{u}{v} \right) = \frac{v \frac{du}{dx} - u \frac{dv}{dx}}{v^2} \quad \rightarrow \quad d \left(\frac{u}{v} \right) = \frac{v \ du - u \ dv}{v^2}$

$\displaystyle \frac{d}{dx}(\sin{u})= \cos{u} \frac{du}{dx} \quad \rightarrow \quad d(\sin{u}) = \cos{u} \ du$

$\displaystyle \frac{d}{dx}(\ln{u})= \frac{1}{u} \frac{du}{dx} \quad \rightarrow \quad d(\ln{x}) = \frac{du}{u}$

Problemas resueltos

Caso 1. Hallando la diferencial de una función

Problema 1. Hallar la diferencial para la función $y = a{x}^{3}$ .

Solución. Derivando la función

$y = a{x}^{3}$

$\displaystyle \frac{dy}{dx} = 3a{x}^{2}$

Despejando las diferenciales

$\therefore dy = 3a{x}^{2} \ dx$

Problema 2. Hallar la diferencial de la siguiente función $y = x{e}^{x}$ .

Solución. Derivando la función

$y = x{e}^{x}$

$\displaystyle \frac{dy}{dx} = {e}^{x} + x{e}^{x}$

$\displaystyle \frac{dy}{dx} = {e}^{x}(1 + x)$

Despejando las diferenciales

$\therefore dy = {e}^{x}(1 + x) \ dx$

Caso 2. Cuando existen valores definidos.

Problema 3. Calcular la diferencial $dy$ de la función $\displaystyle y = \frac{{x}^{2}}{2}$ para $x = 2$ y $dx = 34$ .

Solución. Se empieza a encontrar la diferencial de la función

$\displaystyle y = \frac{{x}^{2}}{2}$

$\displaystyle \frac{dy}{dx} = x$

Despejando las diferenciales

$dy = x \ dx$

Ahora, sustituyendo en los valores de $x$ y $dx$ :

$dy = x \ dx$

$dy = 2(34)$

$dy = 68$

Por lo tanto

$\therefore dy = 68$

Problema 4. Calcular la diferencial $dy$ de la siguiente función $y = \sin{x}$ para $x = 45 \textdegree$ y $dx = 4.0987$ .

Solución. Iniciando con el hallazgo de la diferencial $dy$

$y = \sin{x}$

$\displaystyle \frac{dy}{dx} = \cos{x}$

$dy = \cos{x} \ dx$

Finalmente, sustituyendo los valores correspondientes

$dy = (\cos{45 \textdegree})(4.0987)$

$dy = (0.7071)(4.0987)$

$dy = 2.8982$

Por lo tanto

$\therefore dy = 2.8982$

Caso 3. Cuando se necesita calcular la aproximación de un número irracional.

Problema 5. Calcular el valor aproximado de $\sqrt{51}$ .

Solución. Se tiene lo siguiente

Continuando, se utiliza el valor próximo de $x$ para obtener $y$ .

$\displaystyle y = \sqrt{49}$

$y = 7$

Después, se encuentra la diferencial $dy$ de esa función

$\displaystyle y = \sqrt{x}$

$\displaystyle \frac{dy}{dx} = \frac{1}{2\sqrt{x}}$

$\displaystyle dy = \frac{1}{2\sqrt{x}} \ dx$

Luego, sustituyendo los valores dados

$\displaystyle dy = \frac{1}{2\sqrt{49}}(2)$

$\displaystyle dy = \frac{1}{2(7)}(2)$

$\displaystyle dy = \frac{1}{7}$

Y para finalizar, se realizará una suma con respecto al valor de $y$ y $dy$ siguiente

$\displaystyle \sqrt{51} = y + dy$

$\displaystyle \sqrt{51} = 7 + \frac{1}{7} = \frac{50}{7} \approx 7.1429$

Por lo tanto

$\displaystyle \therefore \sqrt{51} \approx 7.1429$

Problema 6. Calcular el valor aproximado de $\ln{45}$ .

Solución. Se tiene lo siguiente

Continuando, se utiliza el valor próximo de $x$ para obtener $y$

$y = \ln{x}$

$y = \ln{40}$

$y = 3.689$

Después, se obtiene la diferencial de esa función

$y = \ln{x}$

$\displaystyle dy = \frac{1}{x} \ dx$

Luego, sustituyendo los valores dados

$\displaystyle dy = \frac{1}{40} (5)$

$\displaystyle dy = \frac{5}{40}$

$dy =0.125$

Y para finalizar, se realizará una suma con respecto a los valores de $y$ y $dy$ obtenidos anteriormente

$\displaystyle \ln{45} = y + \Delta y$

$\ln{45} = 3.689 + 0.125$

$\ln{45} = 3.814$

Por lo tanto

$\therefore \ln{45} = 3.814$

Caso 4. Aplicaciones de las diferenciales.

Problema 7. Calcular el incremento del área de un cuadrado de 45 pulgadas de lado con un grosor de 0.983 pulgadas.

Solución. Se tiene lo siguiente

Después, se busca la diferencial de esa función

$A ={x}^{2}$

$\displaystyle \frac{dA}{dx} = 2x$

$dA = 2x \ dx$

Finalmente, sustituyendo los valores obtenidos en la tabla

$dA = 2(45 \ \text{pulg})(0.983 \ \text{pulg})$

$dA = 88.47$ pulg²

Por lo tanto, el área aproximada del cuadrado es de 88.47 pulg².

Problema 8. Determinar el volumen aproximado de una cocha esférica cuyo radio interior es de 76 cm y cuyo grosor es de 0.876 cm.

Solución. Se tiene lo siguiente

Después, se determina la diferencial del volumen

$\displaystyle V = \frac{4}{3} \pi {r}^{3}$

$\displaystyle \frac{dV}{dr} = 3 \left(\frac{4}{3} \pi {r}^{2} \right)$

$\displaystyle \frac{dV}{dr} = 4\pi {r}^{2}$

$dV = 4\pi {r}^{2} \ dr$

Finalmente, sustituyendo los valores obtenidos en la tabla

$dV = 4\pi {(76 \ \text{cm})}^{2}(0.876)$

$dV = 20239.104 \pi$ cm³

$\therefore dV = 63583.1691264$ cm³

Por lo tanto, el volumen aproximado de la concha esférica es de 63583.1691264 cm³.

$\displaystyle y=\sqrt{x}$	Función que está representando $\displaystyle \sqrt{51}$
$x=49$	Valor que es próximo para la raíz cuadrada exacta.
$dx = \Delta x = 2$	Incremento para obtener $\displaystyle \sqrt{51}$ , es decir, cuanto le falta para llegar al valor 51.

$\displaystyle y=\ln{x}$	Función que está representando $\displaystyle \ln{45}$
$x=40$	Valor que se acerca a 45
$dx = \Delta x = 5$	Incremento para obtener $\displaystyle \ln{45}$ , es decir, cuanto le falta para llegar al valor 45

$A=x^2$	Función que representa el área de un cuadrado
$x=45$	Valor de la longitud del cuadrado
$dx=\Delta x = 0.983$	Grosor del cuadrado
$dA=\Delta A$	Área aproximada del cuadrado

$\displaystyle V=\frac{4}{3} \pi r^2$	Función que representa el volumen de la concha esférica
$r=76$	Valor del radio de la concha esférica (en cm)
$dr=\Delta r = 0.876$	Grosor de la concha esférica
$dV=\Delta V$	Área aproximada de la concha esférica

La diferencial. Cálculo integral.

Introducción

Problemas resueltos

Caso 1. Hallando la diferencial de una función

Caso 2. Cuando existen valores definidos.

Caso 3. Cuando se necesita calcular la aproximación de un número irracional.

Caso 4. Aplicaciones de las diferenciales.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

La diferencial. Cálculo integral.

Introducción

Problemas resueltos

Caso 1. Hallando la diferencial de una función

Caso 2. Cuando existen valores definidos.

Caso 3. Cuando se necesita calcular la aproximación de un número irracional.

Caso 4. Aplicaciones de las diferenciales.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta