Introducción
La ley de Ohm recibe su nombre por el físico alemán Georg Simon Ohm, quien determinó la relación entre el voltaje y la corriente en una resistencia. La unidad de resistencia lleva su nombre como resultado de su trabajo.
La ley de Ohm establece que a través de una resistencia es directamente proporcional a la corriente que fluye por ella. La resistencia es la constante de proporcionalidad entre el voltaje y la corriente, y se mide en ohms.
La relación matemática de la ley de Ohm se representa por la ecuación
, donde
Esto también se puede representar por la curva característica voltaje-corriente.
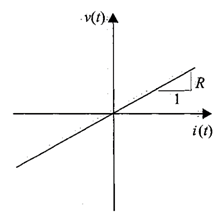
Para representar ohms se utiliza el símbolo Ω, por lo que
1 Ω = 1 V/A
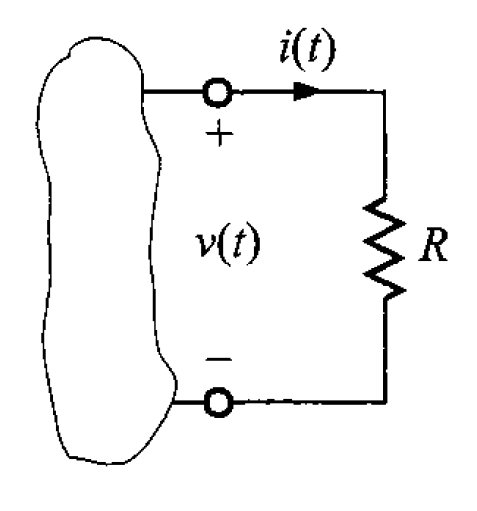
Figura 2. Conexión de una resistencia.
ya que el resistor es un elemento pasivo, la relación de voltaje-corriente apropiada es la siguiente (figura 2). El resistor absorbe la potencia suministrada a las terminales. Se observa que la carga se mueve del potencial mayor al menor conforme pasa a través del resistor, y la energía absorbida la disipa el mismo resistor en forma de calor.
La relación de disipación de energía es la potencia instantánea, y entonces
O también
Esta última ecuación indica que la potencia es una función no lineal, ya sea de la corriente o del voltaje, y siempre la cantidad es positiva.
La conductancia (cuyo símbolo es G) es otra magnitud y es el recíproco de la resistencia.
La unidad de conductancia es el siemens, y la relación entre las unidades es
1 S = 1 A ⋅ V
Se pueden escribir dos expresiones adicionales usando la siguiente ecuación
Cuando la resistencia es nula y cuando es infinita
Hay dos valores de resistencia, y en consecuencia de conductancia, que son muy importantes: R=0 y R=∞.
Se tiene el circuito de la figura 3. Conforme disminuye el valor de la resistencia y se hace cada vez más pequeña, finalmente se alcanza un punto en que es cero y el circuito se reduce al de la figura 4; esto significa que la resistencia puede reemplazarse con un cortocircuito. Por otro lado, si se incrementa el valor de la resistencia, y se hace cada vez más grande, se llega al punto donde es prácticamente infinita y puede ser sustituida por un circuito abierto (figura 5).

Figura 3. Circuito resistivo variable.

Figura 4. Representación de un cortocircuito cuando R=0.
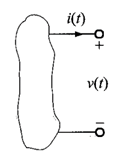
Figura 5. Representación de un circuito abierto cuando R=∞.
Problemas resueltos
Problema 1. En el circuito de la figura 6, encuentre la corriente y la potencia que absorbe el resistor
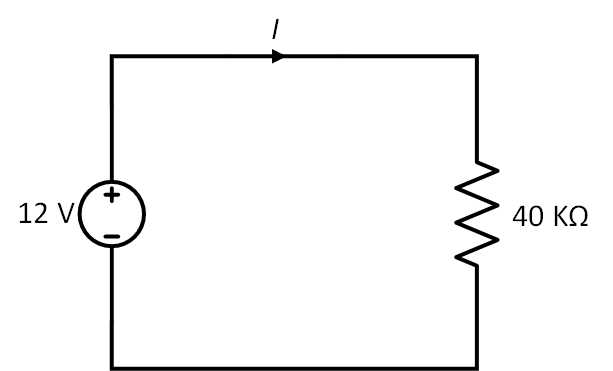
Solución. Por la ley de Ohm
Despejando y sustituyendo
Calculando la potencia
Problema 2. En el circuito de la figura 7, encuentre el voltaje en los extremos de la fuente de corriente y la potencia que suministra dicha fuente.
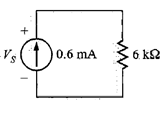
Solución. Observando los datos, se tiene el valor de la corriente y el valor del resistor. Utilizando la ley de Ohm
Calculando su potencia
Problema 3. En el circuito de la figura 8, calcule y
.

Solución. Tomando la fórmula de la potencia
Aplicando la ley de Ohm
Problema 4. En el circuito de la figura 9, calcule y
.
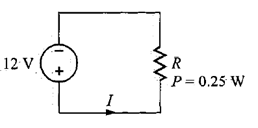
Solución. Usando la fórmula de la potencia
Por último, por la ley de Ohm