Introducción
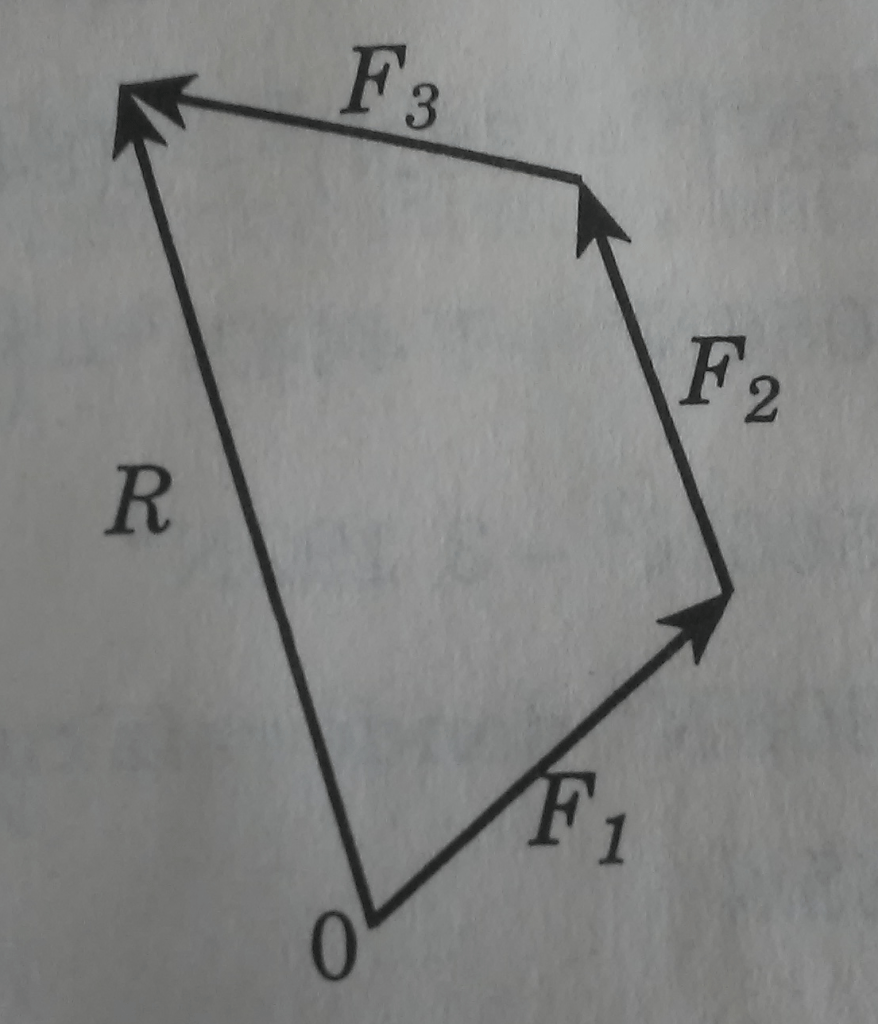
Para sumar más de dos vectores concurrentes en forma gráfica, se utiliza el llamado método del polígono. Este método consiste en trasladar paralelamente a sí mismo cada uno de los vectores sumados, de tal manera que al tomar uno de los vectores como base, los otros se colocarán uno a continuación del otro y así sucesivamente hasta colocar el último. La resultante será el vector que una el origen de los vectores con el extremo libre del último vector sumando, y su sentido estará dirigido hacia el extremo del último vector.
Composición y descomposición de una fuerza en sus componentes rectangulares
Un sistema de vectores puede sustituirse por otro equivalente que contenga un número mayor o menor de vectores que el sistema considerado. Si el sistema equivalente tiene un número mayor de vectores, el procedimiento se llama descomposición. si el sistema equivalente tiene un número menor de vectores, el procedimiento se denomina composición.
La fuerza es toda causa capaz de modificar el estado de reposo o movimiento de un cuerpo. A la acción de empujar o tirar de un cuerpo se le llama fuerza. Por ejemplo, la fuerza forma un ángulo theta (
) con el eje de las
, como se muestra en la figura 2.
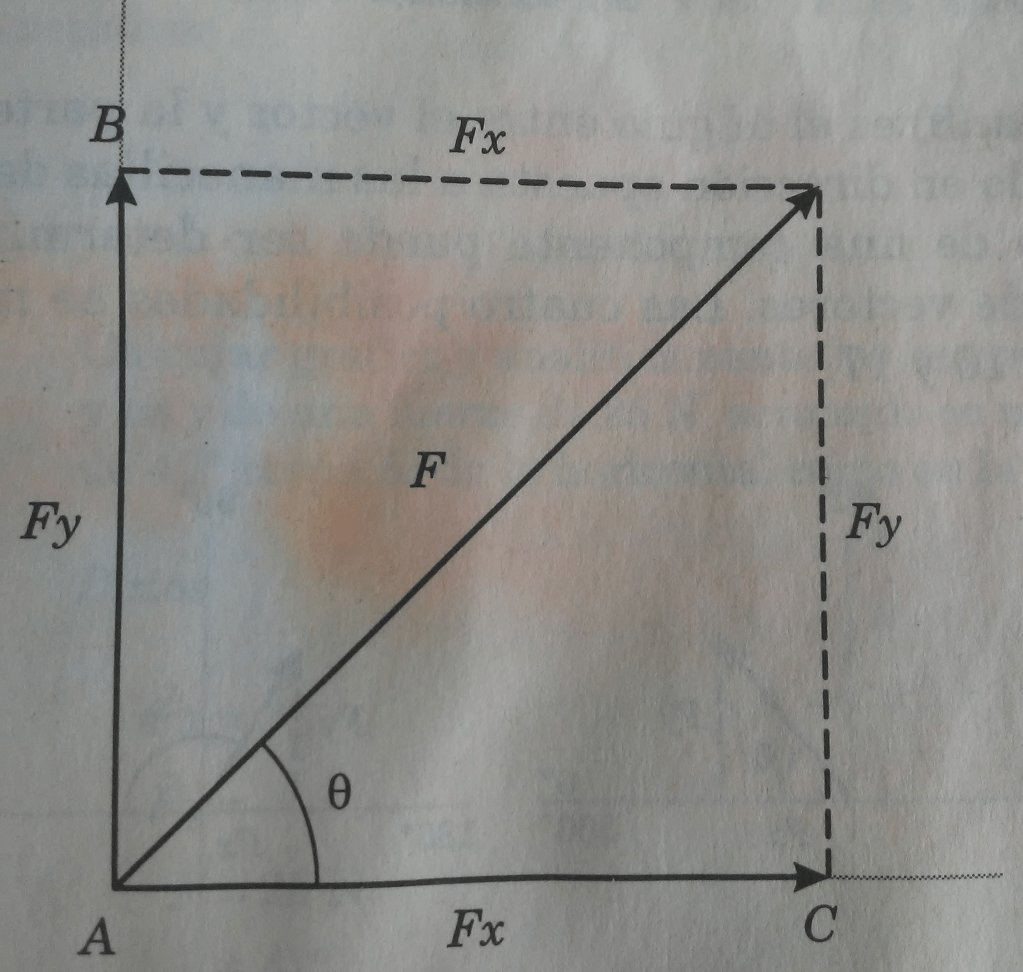
Trazando desde líneas perpendiculares a los ejes
y
, las fuerzas componentes
y
son equivalentes a la fuerza original
, ya que sumándolas vectorialmente dan
como resultante.
Con y
son perpendiculares entre sí, los triángulos OAB y OAC son triángulos rectángulos equivalentes con los correspondientes lados iguales,
y
.
Por trigonometría, se tiene que
Puesto que y
generalmente conocidas, estas ecuaciones son útiles para encontrar las magnitudes de las componentes de la fuerza; despejándolas se obtiene que
donde es el ángulo entre el vector y la parte positiva el eje
medido en dirección opuesta a las manecillas del reloj.
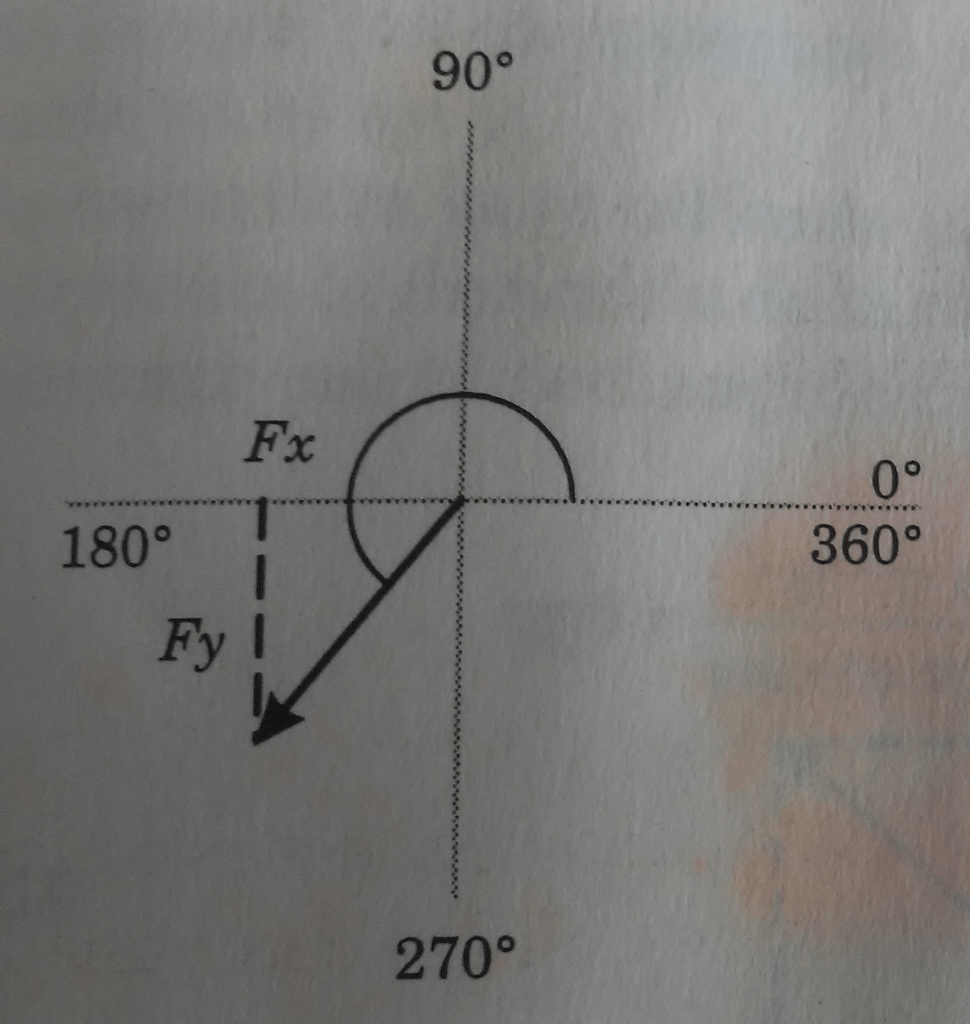
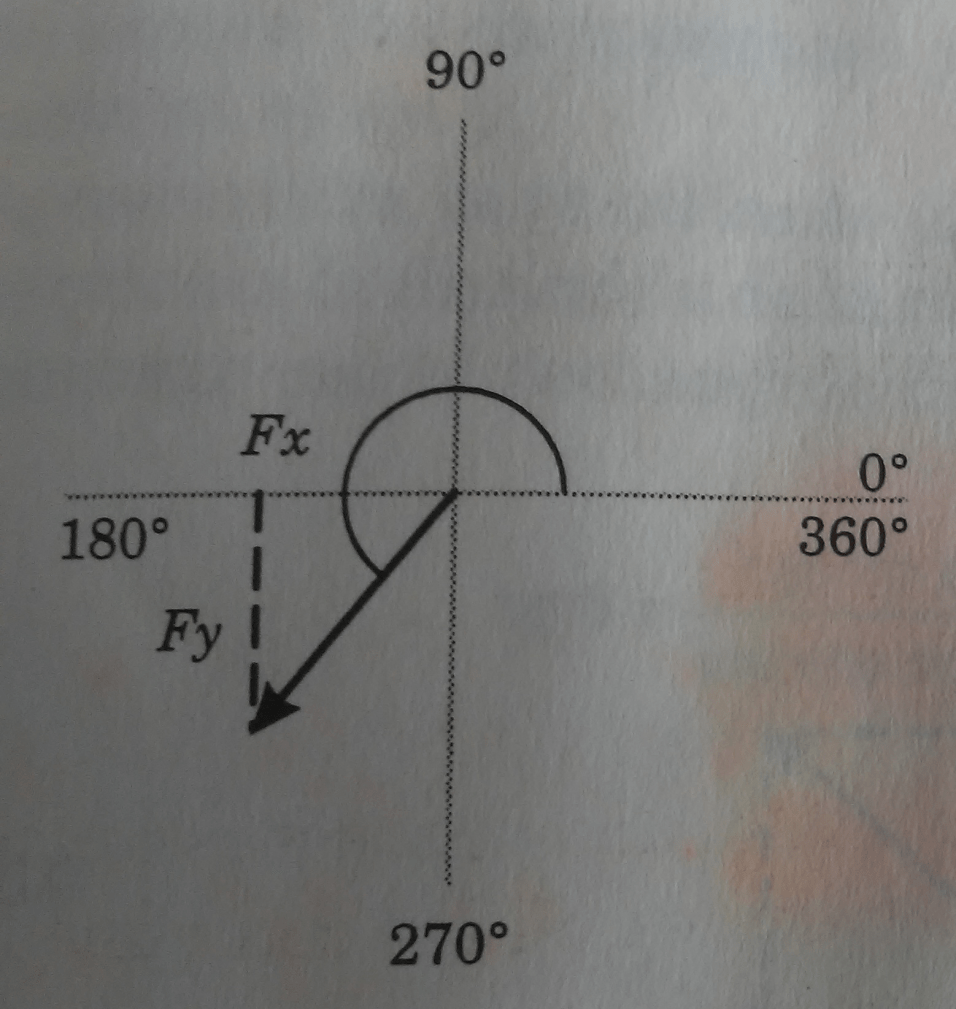
El signo de una componente puede ser determinado de un diagrama de vectores. Las cuatro posibilidades se muestran en las figura 3, 4. 5 y 6.
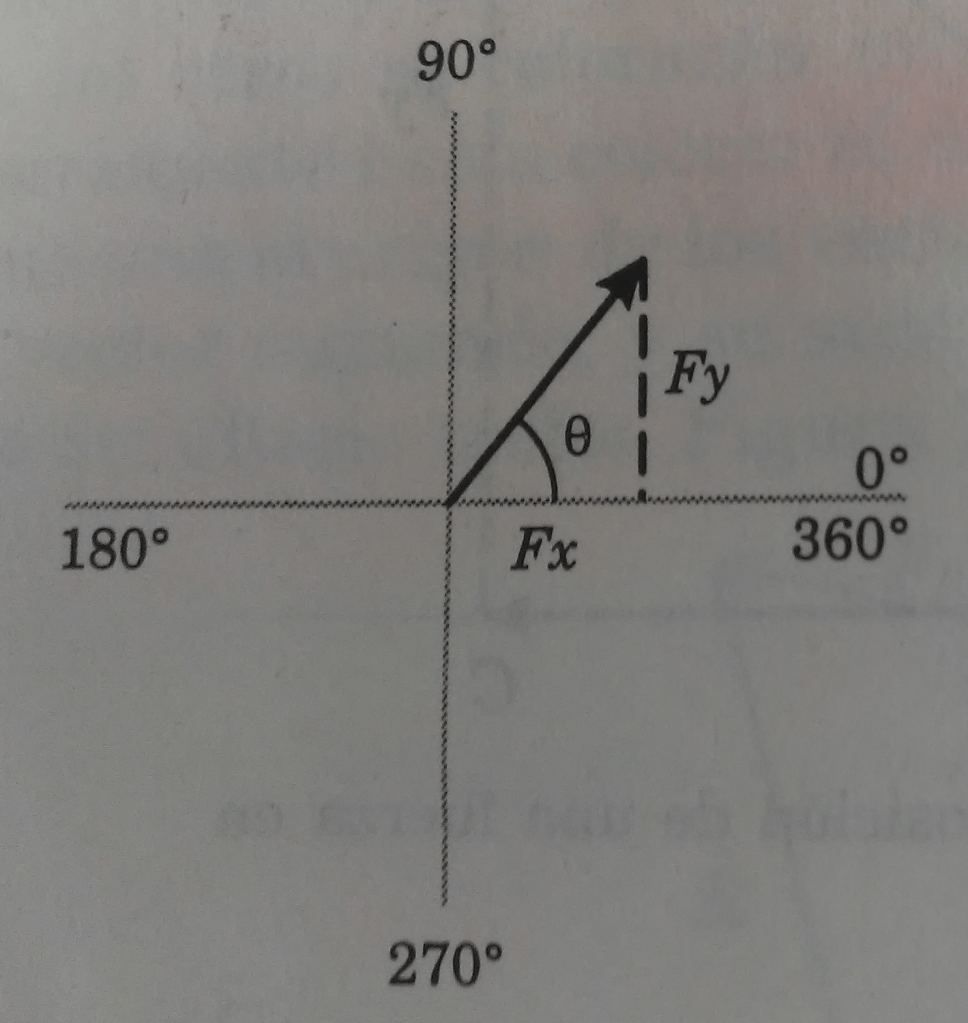
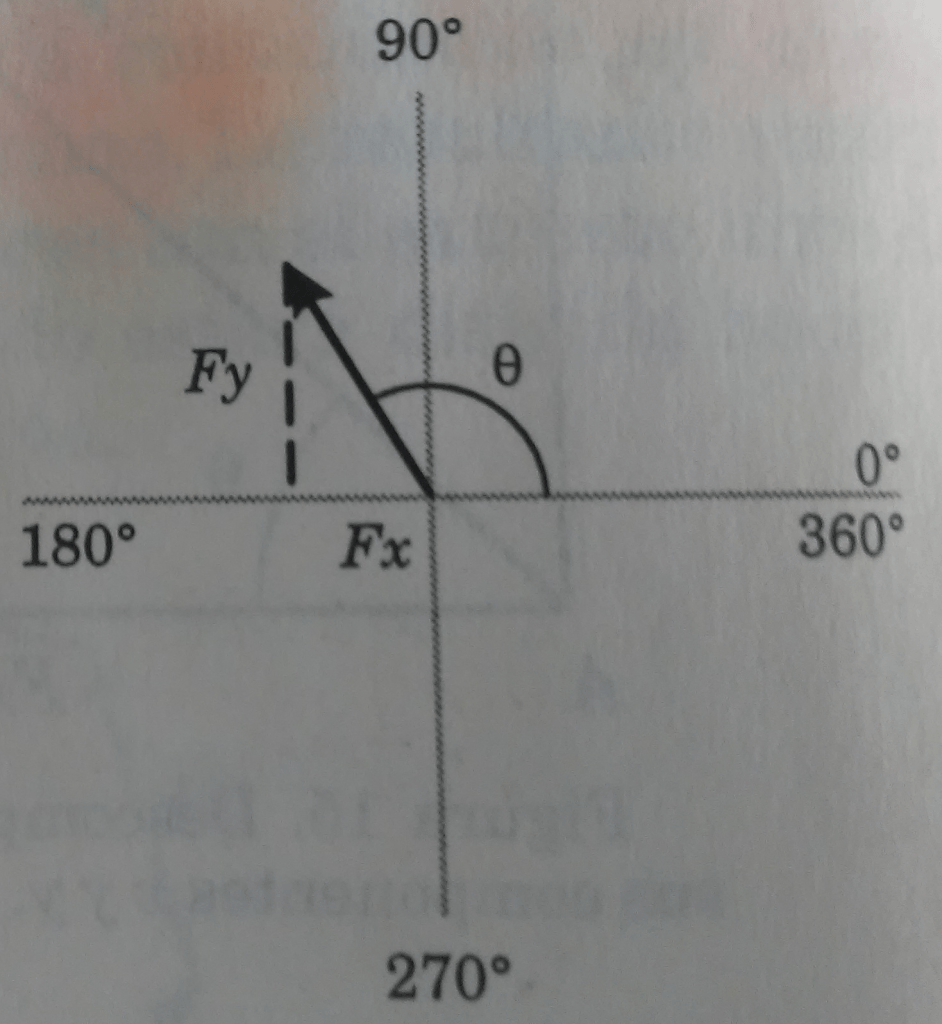
Problemas resueltos
Problema. Calcular gráfica y analíticamente las componentes en y en
de una fuerza de 25 N, actuando en una dirección de 42° respecto de la horizontal como se muestra en la figura 7.
Solución. Se tienen los siguientes datos
°
a) Cálculo gráfico
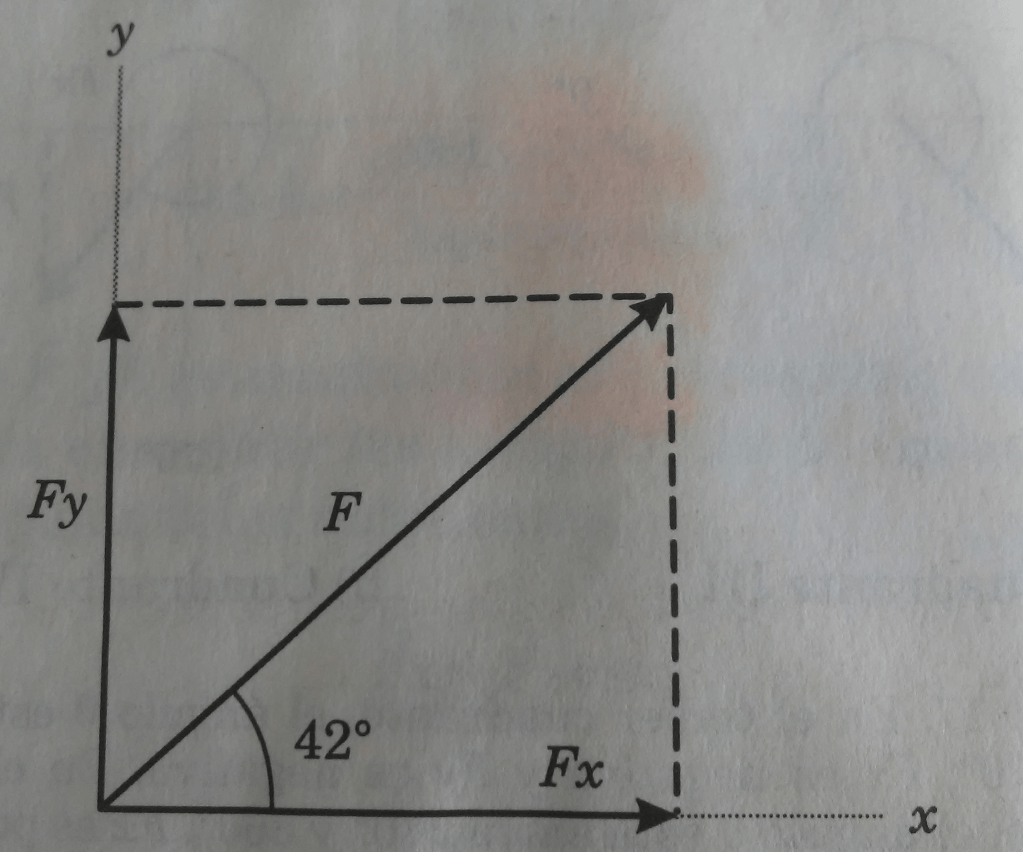
b) Cálculo analítico
Para
Para
Pasos del método de las componentes. Cálculo analítico
Para la solución analítica se realizan las siguientes operaciones:
- Cada fuerza se descompone en sus componentes en el eje
y en el eje
.
- Se suman las componentes
para dar la componente resultante en el eje
.
- Se suman las componentes
para dar la componente resultante en el eje
.
- Se encuentra la resultante usando el Teorema de Pitágoras.
- Se calcula la dirección de la resultante por medio de la función tangente con el rectángulo final.
Problema resuelto
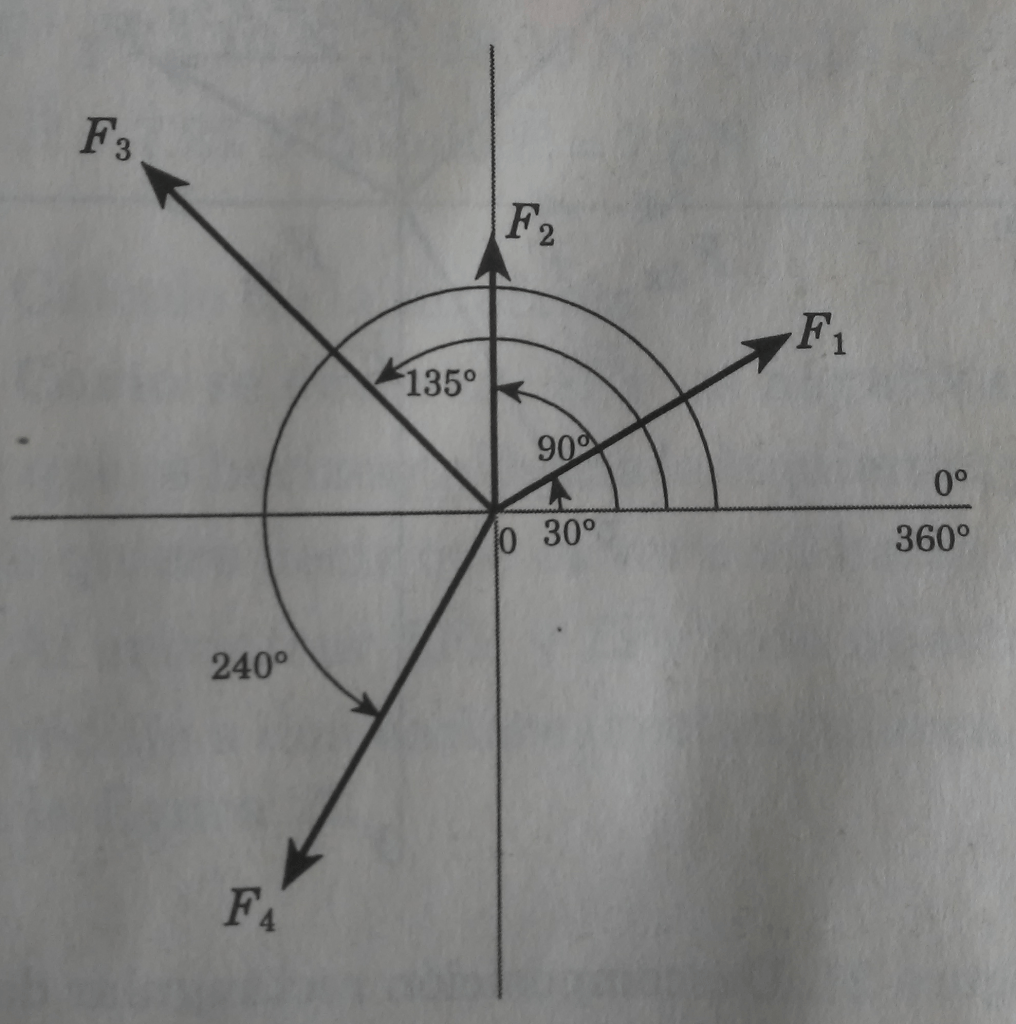
Problema. Calcular gráfica y analíticamente la fuerza resultante equivalente a las siguientes fuerzas (ver los diagramas vectoriales, figuras 8, 9, y 10).
Solución. Los datos son los siguientes:
a 30°
a 90°
a 135°
a 240°
Cálculo gráfico
Método del polígono de fuerzas
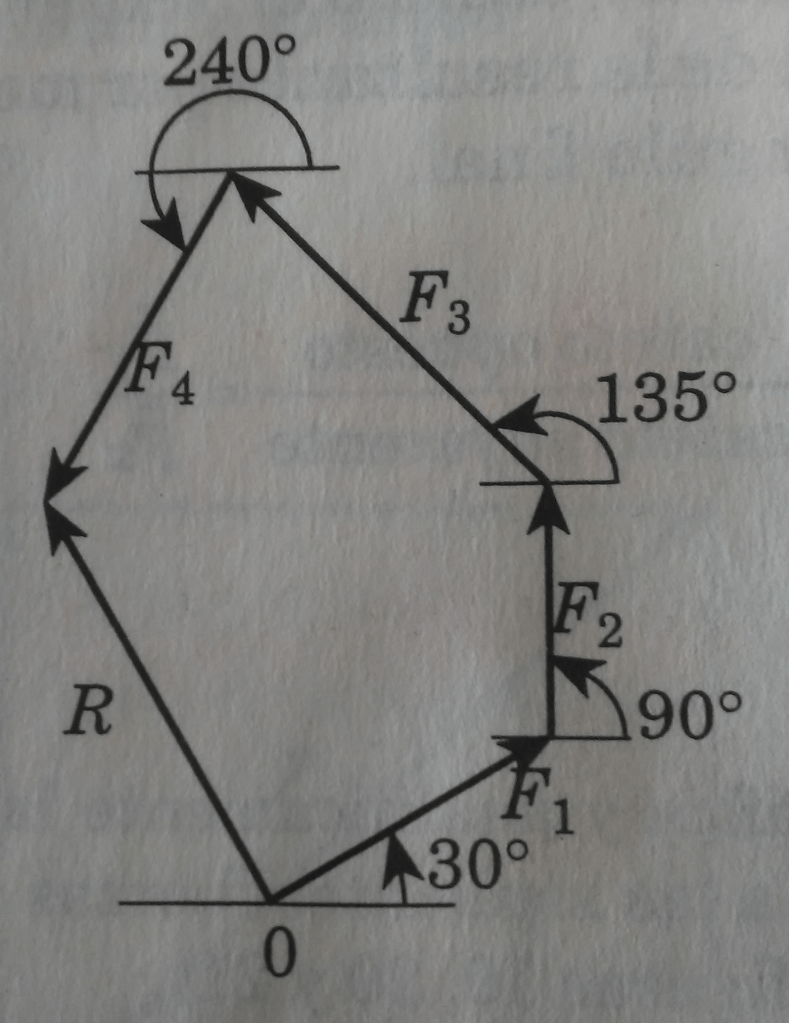
Proyección sobre los ejes x y y

Cálculo analítico
a) Cálculo de la magnitud
La letra griega se llama sigma e indica suma. Entonces
Sustituyendo
Y para se tiene
Sustituyendo
Para obtener la resultante, se utiliza el Teorema de Pitágoras
b) Cálculo de la dirección
Como se observa, es negativa, esto quiere decir que es horizontal hacia la izquierda; y
es positiva, que quiere decir que es vertical hacia arriba.
Al encontrar y
todo nuestro sistema inicial se redujo a dos vectores rectangulares, como se muestra en la figura 11.
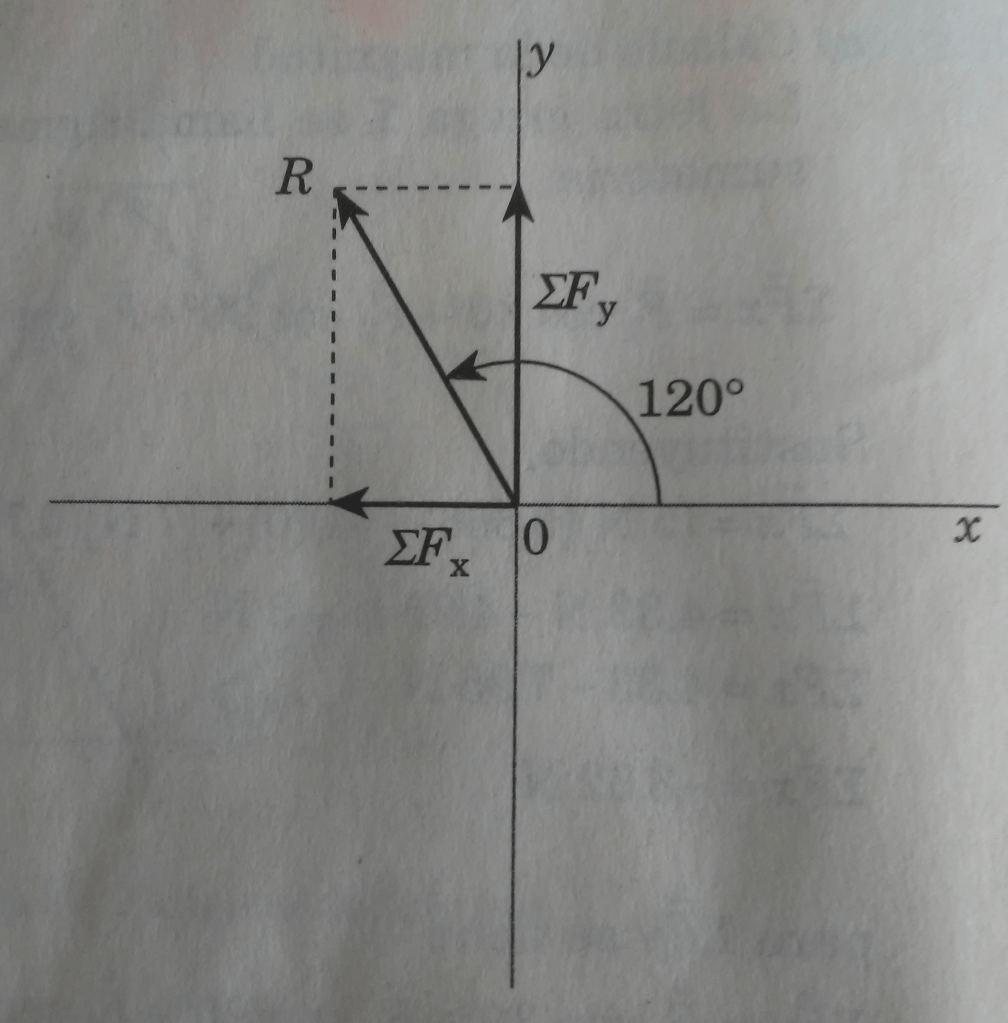
Aplicando la función tangente, se tiene que:
°
Como se observa en la figura_, el vector resultante se encuentra en el segundo cuadrante; entonces,
°