División de corriente para dos resistores (resistencias) y una fuente. Circuitos eléctricos.

Introducción

Un circuito importante es el par de nodos único. En este caso, los elementos tienen el mismo voltaje en sus extremos y, por lo tanto, están en paralelo. Se considera un circuito como el que se muestra en la figura 1, donde tiene una fuente de corriente independiente en paralelo con dos resistores.

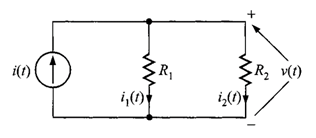
Figura 1. Circuito que ilustra el par de nodos únicos; contiene dos resistores y una fuente de corriente independiente.

En los extremos de cada elemento del circuito aparece el voltaje $v(t)$ , dado que todos ellos están en paralelo.

Al aplicar la ley de Kirchhoff de corriente al nodo superior se obtiene

$-i(t)+i_1 (t)+i_2 (t)=0$

$i(t)=i_1 (t)+i_2 (t)$

Utilizando la ley de Ohm (ya despejado $i(t)$ proveniente de $v(t) = R \cdot i(t)$ )

$\displaystyle i(t) = \frac{v(t)}{R_1} + \frac{v(t)}{R_2} = \left(\frac{1}{R_1} + \frac{1}{R_2} \right) v(t) = \frac{v(t)}{R_P}$

Donde $\displaystyle \frac{1}{R_P} = \frac{1}{R_1} + \frac{1}{R_2}$ o también $\displaystyle R_P = \frac{R_1 R_2}{R_1+R_2}$ .

Por lo tanto, la resistencia equivalente de dos resistores en paralelo es igual al producto de sus resistencias dividido por la suma de las mismas. También se observa que la resistencia equivalente siempre es menor que las resistencias individuales $R_1$ o $R_2$ . En consecuencia, la conexión de resistores en paralelo reduce la resistencia total.

La división de corriente es la manera en la cual la corriente de la fuente i(t) se divide entre las dos romas, y puede hallarse a parte de las siguientes expresiones

$\displaystyle v(t) = R_P \cdot i(t) = \left( \frac{R_1 R_2}{R_1+R_2} \right) i(t)$

$\displaystyle i_1 (t) = \frac{v(t)}{R_1} = \frac{R_P \cdot i(t)}{R_1} = \frac{R_2}{R_1+R_2} \cdot i(t)$

$\displaystyle i_2 (t) = \frac{v(t)}{R_2} = \frac{R_P \cdot i(t)}{R_2} = \frac{R_1}{R_1+R_2} \cdot i(t)$

Problema resuelto

Problema 1. Encuentre $I_1$ , $I_2$ y $V_o$ para la red de la figura 2.

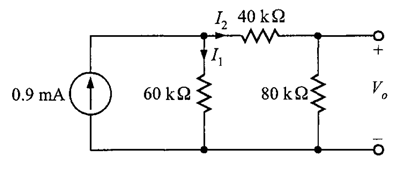
Solución. Primero, es importante identificar que la fuente de corriente alimenta dos trayectorias en paralelo. Para enfatizar este punto, el circuito se dibuja nuevamente (figura 3).

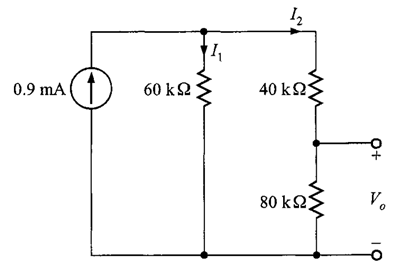
Figura 3. Modificación del circuito de la figura 2.

Al aplicar la división de corriente se obtiene, la corriente $I_1$ es

$\displaystyle I_1 = \left[\frac{40 \ \text{k} + 80 \ \text{k}}{60 \ \text{k} + (40 \ \text{k} + 80 \ \text{k})} \right] (0.9 \ \text{m})$

$\displaystyle I_1 = \left[\frac{40 \times 10^3 + 80 \times 10^3}{60 \times 10^3 + (40 \times 10^3 + 80 \times 10^3)} \right] (0.9 \times 10^{-3})$

$\therefore I_1 = 0.6 \ \text{mA}$

e $I_2$ es

$\displaystyle I_2 = \left[\frac{60 \ \text{k}}{60 \ \text{k} + (40 \ \text{k} + 80 \ \text{k})} \right] (0.9 \ \text{m})$

$\displaystyle I_2 = \left[ \frac{60 \times 10^3}{60 \times 10^3 + (40 \times 10^3 + 80 \times 10^3)} \right] (0.9 \times 10^{-3})$

$\therefore I_2 = 0.3 \ \text{mA}$

Se observa que por el resistor menor fluye la corriente mayor, y viceversa. Además, las resistencias de las dos trayectorias son iguales, la corriente se divide por igual entre ellas. Ya que $I_1+I_2 = 0.6 \ \text{mA} + 0.3 \ \text{mA} =0.9 \ \text{mA}$ , se cumple la LKC.