Área bajo una curva utilizando sumas. Cálculo integral.

Introducción

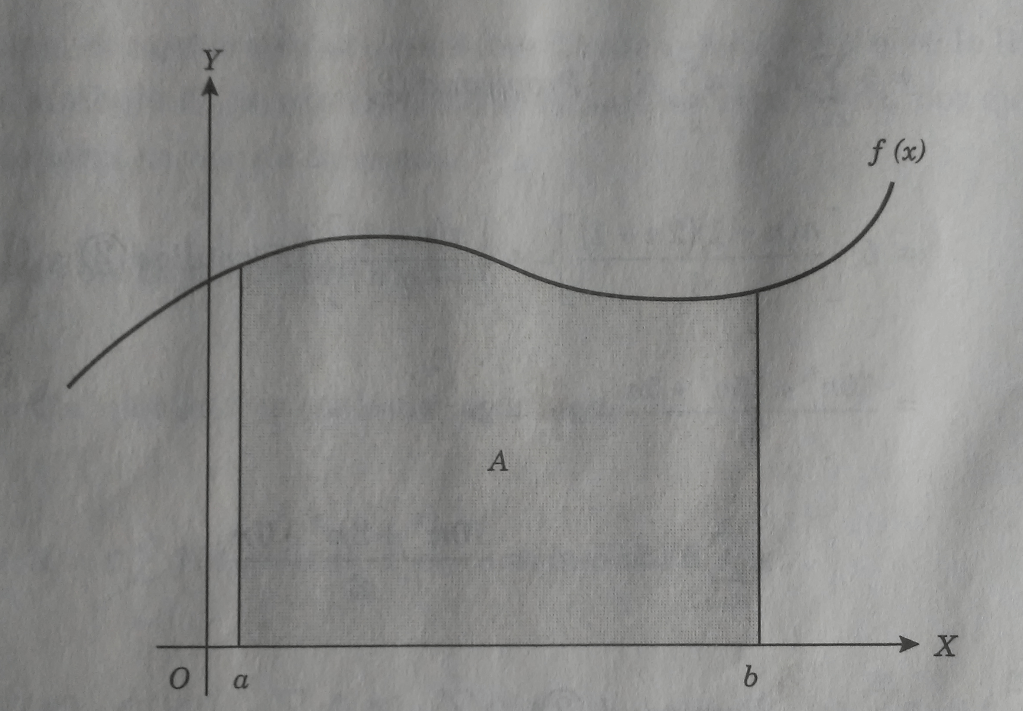
Para obtener el área de una región en el plano cartesiano, la cual está limitada por el eje de las $X$ , las rectas $x=a$ y $x=b$ y la curva $f(x)$ , donde $f$ es una función continua en el intervalo cerrado $[a,b]$ (figura 1); sea $A$ el área de una región del plano cartesiano.

Una primera manera aproximada consiste en calcular el área de la región rectangular sombreada (figura 2).

Se considera dos regiones rectangulares, para mejorar la aproximación del área buscada (figura 3).

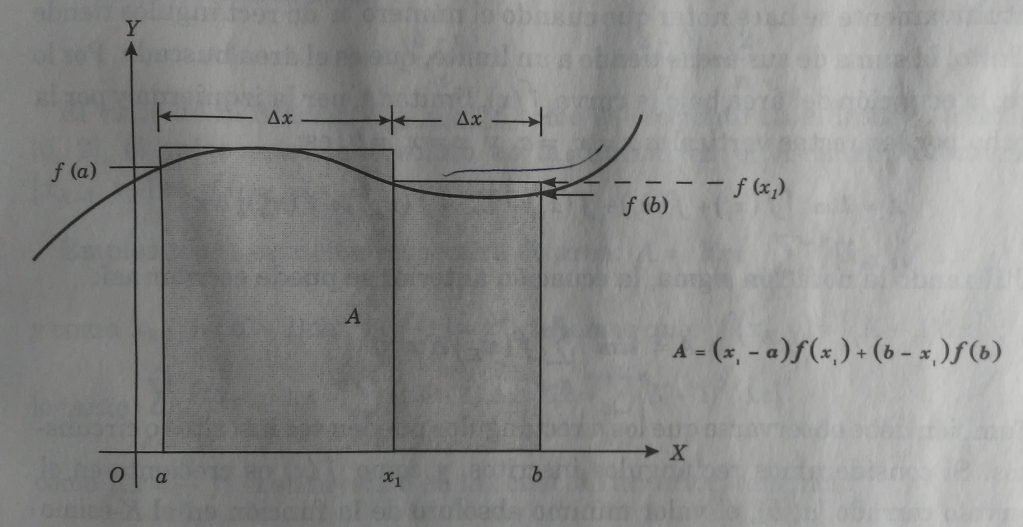
Si los dos subintervalos en que se divide el intervalo $[a,b]$ tienen la misma longitud, es decir, $\Delta x = (x_1 - a) = (b-x_1)$ , la ecuación anterior se puede escribir de esta manera:

$\displaystyle A = \Delta x \cdot f(x_1) + \Delta x \cdot f(b) = [f(x_1) + f(b)] \Delta x$

A medida que el número de regiones rectangulares aumenta, la diferencia entre la suma de sus áreas y el área bajo la curva disminuye.

Dividiendo el intervalo cerrado $[a,b]$ en $n$ subintervalos de igual longitud ( $\Delta x$ ), de manera que $\displaystyle \Delta x = \frac{a-b}{n}$ (figura 4).

Por lo tanto, la ecuación de la suma de las áreas de los $n$ rectángulos es:

$\displaystyle A = \left[f(x_1) + f(x_2) + f(x_3) + \cdots + f(x_{n+1}) + f(x_n) \right] \Delta x$

Intuitivamente se hace notar que cuando el número $n$ de rectángulos tiende a infinito, la suma de sus áreas tiende a un límite, que es el área buscada. Por lo tanto, la ecuación del área bajo la curva $f(x)$ , limitada por la izquierda y por la derecha por las rectas verticales $x=x_0=a$ y $x=x_n=b$ , es

$\displaystyle A = \lim_{n \rightarrow + \infty}{\left[f(x_1) + f(x_2) + f(x_3) + \cdots + f(x_{n+1}) + f(x_n) \right] \Delta x}$

Utilizando la notación sigma, la ecuación anterior se puede escribir así

$\displaystyle A = \lim_{n \rightarrow + \infty}{\sum_{k=1}^n{f(x_k) \cdot \Delta x}}$

También debe observarse que los $n$ rectángulos pueden ser inscritos o circunscritos. si se considera rectángulos inscritos, y como $f(x)$ es creciente en el intervalo cerrado $[a,b]$ , el valor mínimo absoluto de la función en el k-enésimo subintervalo $[x_{k-1}, x_k]$ es $f(x_{k-1})$ , por lo que la ecuación del área bajo la curva es

$\displaystyle A = \lim_{n \rightarrow + \infty}{\sum_{k=1}^n{f(x_{k-1}) \cdot \Delta x}}$

Las sumas correspondientes de las áreas de los rectángulos circunscritos son, por lo menos, tan grandes como el área de la región $A$ , y se puede demostrar que el límite de estas sumas cuando $n$ crece sin límite es exactamente el mismo que el límite de la suma de las áreas de los rectángulos inscritos. El valor máximo absoluto de la función en el k-ésimo subintervalo $[x_{k-1},x_k]$ es $f(x_k)$ , por lo que la ecuación del área bajo la curva dividida por rectángulos circunscritos es

$\displaystyle A = \lim_{n \rightarrow + \infty}{\sum_{k=1}^n{f(x_k) \cdot \Delta x}}$

Problema resuelto

Problema 1. Hallar el área de la región limitada por la curva $y=x^2$ , el eje $X$ y la recta $x=2$ , tomando: a) rectángulos inscritos, b) rectángulos circunscritos.

Solución. Se grafica la curva y la recta mencionada.

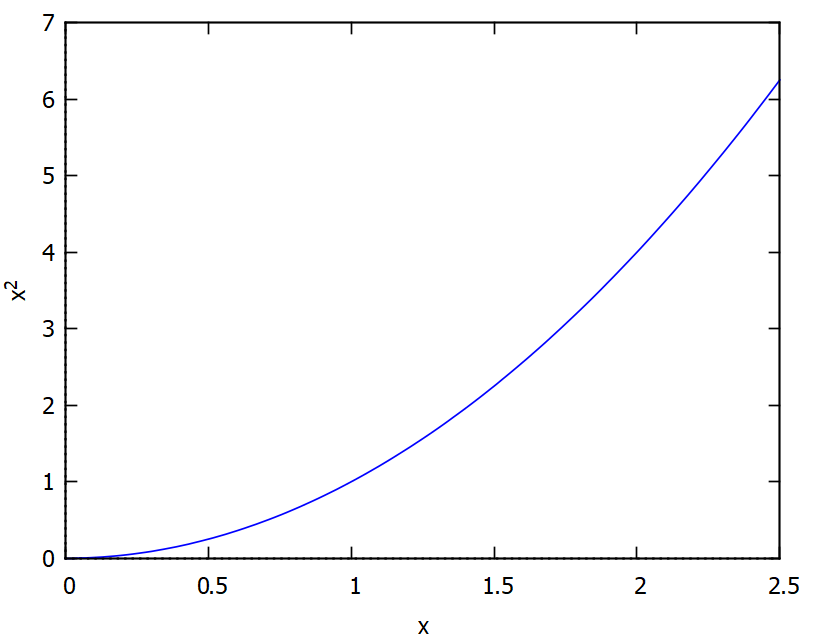
Solución del a). Al dividir el intervalo cerrado $[0,2]$ en $n$ subintervalos, cada uno con longitud $\Delta x$ , es decir

$\displaystyle \Delta x = \frac{b-a}{n} = \frac{2-0}{n} = \frac{2}{n}$

El valor de la función es $y=x^2$ , como es creciente en el intervalo cerrado $[0,2]$ , el valor mínimo absoluto de la función en el k-ésimo subintervalo $[x_{k-1},x_k]$ es $f(x_{k-1})$ . Luego, se grafica la función con el rectángulo inscrito en la función dada por el problema como referencia.

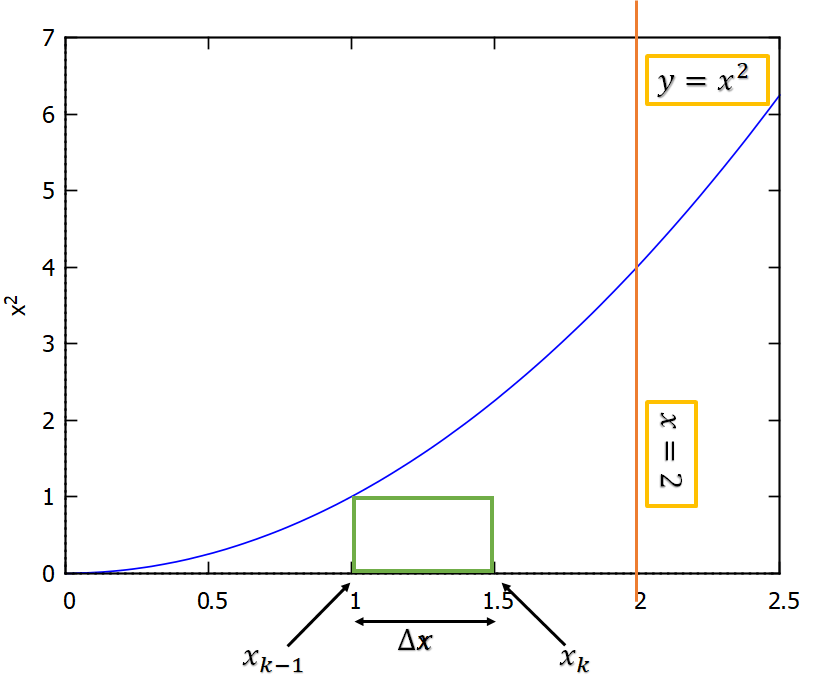
Empleando la ecuación respectiva de área para rectángulos inscritos es

$\displaystyle A = \lim_{n \rightarrow + \infty}{\sum_{k=1}^n{f({k-1}) \cdot \Delta x}}$

y como $x_{k-1} = \left(k-1 \right) \Delta x$ y $f(x) = x^2$ , se tiene que

$\displaystyle f(x_{k-1}) = {\left[ \left(k-1 \right) \Delta x \right]}^2$

$\displaystyle f(x_{k-1}) = {\left(k-1 \right)}^2 {\left(\Delta x \right)}^2$

$\displaystyle f(x_{k-1}) = \left(k^2 -2k + 1 \right) {\left(\Delta x \right)}^2$

Utilizando la fórmula para calcular el área bajo una curva utilizando rectángulos inscritos y sustituyendo

$\displaystyle A = \lim_{n \rightarrow + \infty}{\sum_{k=1}^n{f(x_{k-1}) \cdot \Delta x}}$

$\displaystyle A = \lim_{n \rightarrow + \infty}{\sum_{k=1}^n{\left(k^2 -2k + 1 \right) {\left(\Delta x \right)}^2 \cdot \Delta x}} = \lim_{n \rightarrow + \infty}{\sum_{k=1}^n{\left(k^2 -2k + 1 \right) {\left(\Delta x \right)}^3}}$

$\displaystyle A = \lim_{n \rightarrow + \infty}{\sum_{k=1}^n{\left(k^2 -2k + 1 \right) {\left(\frac{2}{n} \right)}^3}} = \lim_{n \rightarrow + \infty}{\sum_{k=1}^n{\left(k^2 -2k + 1 \right) \left(\frac{8}{n^3} \right)}}$

$\displaystyle A = \lim_{n \rightarrow + \infty}{\sum_{k=1}^n{\left(\frac{8}{n^3} k^2 - \frac{16}{n^3} k + \frac{8}{n^3} \right) }} = \lim_{n \rightarrow + \infty}{\left[\frac{8}{n^3} \sum_{k=1}^n{k^2} - \frac{16}{n^3} \sum_{k=1}^n{k} + \frac{8}{n^3} \sum_{k=1}^n{1} \right]}$

$\displaystyle A = \lim_{n \rightarrow + \infty}{\left\{\frac{8}{n^3} \left[\frac{n(n+1)(2n+1)}{6} \right] - \frac{16}{n^3} \left[\frac{n(n+1)}{2} \right] + \frac{8}{n^3} (n) \right\}}$

$\displaystyle A = \lim_{n \rightarrow + \infty}{\left\{\frac{8}{n^3} \left[\frac{(n^2+n)(2n+1)}{6} \right] - \frac{16}{n^3} \left(\frac{n^2+n}{2} \right) + \frac{8n}{n^3} \right\}}$

$\displaystyle A = \lim_{n \rightarrow + \infty}{\left[\frac{8}{n^3} \left(\frac{2n^3+3n^2+n}{6} \right) - \frac{16}{n^3} \left(\frac{n^2+n}{2} \right) + \frac{8n}{n^3} \right]}$

$\displaystyle A = \lim_{n \rightarrow + \infty}{\left[\frac{8}{n^3} \left(\frac{2n^3+3n^2+n}{6} \right) - \frac{16}{n^3} \left(\frac{3n^2+3n}{6} \right) + \frac{48n}{6n^3} \right]}$

$\displaystyle A = \lim_{n \rightarrow + \infty}{\left[\frac{16n^3+24n^2+8n}{6n^3} - \left(\frac{48n^2+48n}{6n^3} \right) + \frac{48n}{6n^3} \right]}$

$\displaystyle A = \lim_{n \rightarrow + \infty}{\left(\frac{16n^3+24n^2+8n - 48n^2-48n + 48n}{6n^3} \right)} = \lim_{n \rightarrow + \infty}{\left(\frac{16n^3-24n^2+8n}{6n^3} \right)}$

$\displaystyle A = \lim_{n \rightarrow + \infty}{\left(\frac{16n^3}{6n^3} - \frac{24n^2}{6n^3}+\frac{8n}{6n^3} \right)} = \lim_{n \rightarrow + \infty}{\left(\frac{8}{3} - \frac{4}{n}+\frac{4}{3n^2} \right)}$

$\displaystyle A = \lim_{n \rightarrow + \infty}{\frac{8}{3}} - \lim_{n \rightarrow + \infty}{\frac{4}{n}} + \lim_{n \rightarrow + \infty}{\frac{4}{3n^2}} = \frac{8}{3} - 0 + 0 = \frac{8}{3}$

$\displaystyle \therefore A = \frac{8}{3} \ \text{u}^2$

Por lo tanto, el área de la región es de 8/3 de unidades cuadradas.

Solución del b). El valor máximo absoluto de la función en el k-ésimo subintervalo $[x_{k-1},x_k]$ es $f(x_k)$ . A continuación, se grafica la función con el rectángulo circunscrito en la función dada por el problema como referencia.

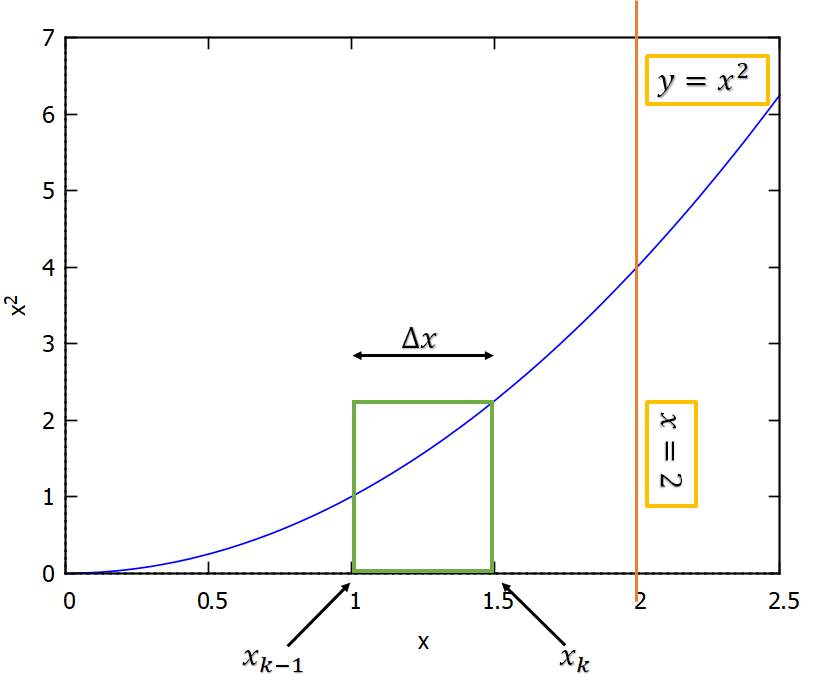
Empleando la ecuación respectiva de área para rectángulos circunscritos

$\displaystyle A = \lim_{n \rightarrow + \infty}{\sum_{k=1}^n{f(x_k) \cdot \Delta x}}$

y como $x_k=k \ \Delta x$ y $f(x)=x^2$ , se tiene que

$\displaystyle f(x_k) = {(k \ \Delta x)}^2$

$\displaystyle f(x_k) = k^2 \ {(\Delta x)}^2$

Sustituyendo en la fórmula anterior

$\displaystyle A = \lim_{n \rightarrow + \infty}{\sum_{k=1}^n{f(x_k) \cdot \Delta x}}$

$\displaystyle A = \lim_{n \rightarrow + \infty}{\sum_{k=1}^n{k^2 \ {(\Delta x)}^2 \cdot \Delta x}} = \lim_{n \rightarrow + \infty}{\sum_{k=1}^n{k^2 \ {(\Delta x)}^3}}$

Recordando que $\displaystyle \Delta x = \frac{2}{n}$

$\displaystyle A = \lim_{n \rightarrow + \infty}{\sum_{k=1}^n{k^2 { \left( \frac{2}{n} \right)}^3}} = \lim_{n \rightarrow + \infty}{\sum_{k=1}^n{k^2 \left( \frac{8}{n^3} \right)}}$

$\displaystyle A = \lim_{n \rightarrow + \infty}{\left(\frac{8}{n^3} \sum_{k=1}^n{k^2} \right)} = \lim_{n \rightarrow + \infty}{\left\{\frac{8}{n^3} \left[\frac{n(n+1)(2n+1)}{6} \right] \right\}}$

$\displaystyle A = \lim_{n \rightarrow + \infty}{\left\{\frac{8}{n^3} \left[\frac{(n^2+n)(2n+1)}{6} \right] \right\}} = \lim_{n \rightarrow + \infty}{\left[\frac{8}{n^3} \left( \frac{2n^3+3n^2+n}{6} \right) \right]}$

$\displaystyle A = \lim_{n \rightarrow + \infty}{\left( \frac{16n^3+24n^2+8n}{6n^3} \right) } = \lim_{n \rightarrow + \infty}{\left( \frac{16n^3}{6n^3} + \frac{24n^2}{6n^3} + \frac{8n}{6n^3} \right) }$

$\displaystyle A = \lim_{n \rightarrow + \infty}{\left( \frac{8}{3} + \frac{4}{n} + \frac{4}{3n^2} \right) } = \lim_{n \rightarrow + \infty}{\frac{8}{3}} + \lim_{n \rightarrow + \infty}{\frac{4}{n}} + \lim_{n \rightarrow + \infty}{\frac{4}{3n^2}} = \frac{8}{3} + 0+ 0 = \frac{8}{3}$

$\displaystyle \therefore A = \frac{8}{3} \ \text{u}^2$

Por lo tanto, el área de la región es de 8/3 de unidades cuadradas.

Área bajo una curva utilizando sumas. Cálculo integral.

Introducción

Problema resuelto

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Área bajo una curva utilizando sumas. Cálculo integral.

Introducción

Problema resuelto

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta