Introducción

Se tiene el circuito mostrado en la figura 1. La dirección de las corrientes se asume tal como se ilustra en la figura.

Figura 1. Circuito con cuatro nodos.

Aplicando la LKC en el nodo 1, se tiene

\displaystyle \sum_{j=1}^{n}{i_j} = 0

\displaystyle i_1 -i_3 - i_A + i_2 = 0

\displaystyle \frac{v_1}{R_1} - \frac{v_3-v_1}{R_3} - i_A + \frac{v_1 - v_2}{R_2} = 0

\displaystyle \frac{v_1}{R_1} - \frac{v_3}{R_3} - \frac{v_1}{R_3} - i_A + \frac{v_1}{R_2} - \frac{v_2}{R_2} = 0

\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \right) v_1 - \left(\frac{1}{R_2} \right) v_2 - \left(\frac{1}{R_3} \right) v_3 = i_A

Figura 2. Señalando el nodo 1 para el análisis de LKC.

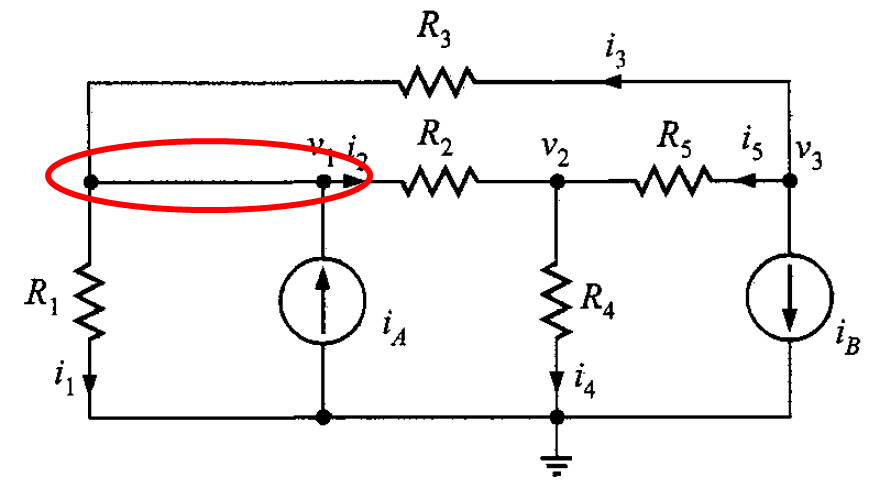
Al usar la LKC en el nodo 2, resulta

\displaystyle \sum_{j=1}^{n}{i_j} = 0

\displaystyle -i_2 + i_4 - i_5 = 0

\displaystyle -\frac{v_1 - v_2}{R_2} + \frac{v_2}{R_4} - \frac{v_3-v_2}{R_5} = 0

\displaystyle -\frac{v_1}{R_2} + \frac{v_2}{R_2} + \frac{v_2}{R_4} - \frac{v_3}{R_5} + \frac{v_2}{R_5} = 0

\displaystyle - \left(\frac{1}{R_2} \right) v_1 + \left(\frac{1}{R_2} + \frac{1}{R_4} + \frac{1}{R_5} \right) v_3 - \left(\frac{1}{R_5} \right) v_3 = 0

Figura 3. Señalando el nodo 2 para el análisis de LKC.

Al usar la LKC en el nodo 3, resulta

\displaystyle \sum_{j=1}^{n}{i_j} = 0

\displaystyle i_B + i_5 + i_3 = 0

\displaystyle i_B + \frac{v_3 - v_2}{R_5} + \frac{v_3-v_1}{R_3} = 0

\displaystyle i_B + \frac{v_3}{R_5} - \frac{v_2}{R_5} + \frac{v_3}{R_3} - \frac{v_1}{R_3} = 0

\displaystyle - \left(\frac{1}{R_3} \right) v_1 - \left(\frac{1}{R_5} \right) v_2 + \left(\frac{1}{R_3} + \frac{1}{R_5} \right) v_3 = - i_B

Figura 4. Señalando el nodo 3 para el análisis de LKC.

Así que, las ecuaciones obtenidas son

\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \right) v_1 - \left(\frac{1}{R_2} \right) v_2 - \left(\frac{1}{R_3} \right) v_3 = i_A
\displaystyle - \left(\frac{1}{R_2} \right) v_1 + \left(\frac{1}{R_2} + \frac{1}{R_4} + \frac{1}{R_5} \right) v_3 - \left(\frac{1}{R_5} \right) v_3 = 0
\displaystyle - \left(\frac{1}{R_3} \right) v_1 - \left(\frac{1}{R_5} \right) v_2 + \left(\frac{1}{R_3} + \frac{1}{R_5} \right) v_3 = - i_B

Recordando que \displaystyle G= \frac{1}{R}, el conjunto de ecuaciones tiene la siguiente forma

\displaystyle \left(G_1 + G_2 + G_3 \right) v_1 - G_2 v_2 - G_3 v_3 = i_A
\displaystyle - G_2 v_1 + \left(G_2 + G_4 + G_5 \right) v_3 - G_5 v_3 = 0
\displaystyle - G_3 v_1 - G_5 v_2 + \left(G_3 + G_5 \right) v_3 = - i_B

Se observa que el análisis produce tres ecuaciones simultáneas en las incógnitas v_1, v_2 y v_3 y se resolverá por medio de análisis matricial.

La forma general general de la ecuación matricial es

\displaystyle \bold{G} \bold{V} = \bold{I}

La solución de la ecuación matricial es

\displaystyle \bold{V} = \bold{G}^{-1} \bold{I}

donde la matriz inversa de \bold{G} se calcula teniendo los resultados de su matriz adjunta traspuesta y de su determinante, es decir

\displaystyle \bold{G}^{-1} = \frac{{(Adj \ \bold{G})}^T}{\text{det} \ \bold{G}} = \left(\frac{1}{\text{det} \ \bold{G}} \right) {(Adj \ \bold{G})}^T

El determinante de la matriz \bold{G} se calcula como

\displaystyle \text{det} \ \bold{G} = |\bold{G}|

\displaystyle \text{det} \ \bold{G} = \left|\begin{matrix} g_{11} & g_{12} & g_{13} \\ g_{21} & g_{22} & g_{23} \\ g_{31} & g_{32} & g_{33} \end{matrix} \right|

\displaystyle \text{det} \ \bold{G} = \left(g_{11} g_{22} g_{33} + g_{12} g_{23} g_{31} + g_{13} g_{21} g_{32} \right) - \left(g_{31} g_{22} g_{13} + g_{32} g_{23} g_{11} + g_{33} g_{21} g_{12} \right)

La matriz adjunta de \bold{G} se calcula como

\displaystyle Adj \ \bold{G} = \left[\begin{matrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{matrix} \right]

donde C_{ij} es el cofactor correspondiente y se calcula utilizando la fórmula

\displaystyle C_{ij} = {(-1)}^{i+j} \ M_{ij}

donde M_{ij} es el menor del elemento g_{ij} y para encontrar el valor de cada menor, se realiza lo siguiente

\displaystyle M_{11} = \left|\begin{matrix} \bold{g_{11}} & \bold{g_{12}} & \bold{g_{13}} \\ \bold{g_{21}} & g_{22} & g_{23} \\ \bold{g_{31}} & g_{32} & g_{33} \end{matrix} \right| = \left|\begin{matrix} g_{22} & g_{23} \\ g_{32} & g_{33} \end{matrix} \right|\displaystyle M_{12} = \left|\begin{matrix} \bold{g_{11}} & \bold{g_{12}} & \bold{g_{13}} \\ g_{21} & \bold{g_{22}} & g_{23} \\ g_{31} & \bold{g_{32}} & g_{33} \end{matrix} \right| = \left|\begin{matrix} g_{21} & g_{23} \\ g_{31} & g_{33} \end{matrix} \right|\displaystyle M_{13} = \left|\begin{matrix} \bold{g_{11}} & \bold{g_{12}} & \bold{g_{13}} \\ g_{21} & g_{22} & \bold{g_{23}} \\ g_{31} & g_{32} & \bold{g_{33}} \end{matrix} \right| = \left|\begin{matrix} g_{21} & g_{22} \\ g_{31} & g_{32} \end{matrix} \right|
\displaystyle M_{21} = \left|\begin{matrix} \bold{g_{11}} & g_{12} & g_{13} \\ \bold{g_{21}} & \bold{g_{22}} & \bold{g_{23}} \\ \bold{g_{31}} & g_{32} & g_{33} \end{matrix} \right| = \left|\begin{matrix} g_{12} & g_{13} \\ g_{32} & g_{33} \end{matrix} \right|\displaystyle M_{22} = \left|\begin{matrix} g_{11} & \bold{g_{12}} & g_{13} \\ \bold{g_{21}} & \bold{g_{22}} & \bold{g_{23}} \\ g_{31} & \bold{g_{32}} & g_{33} \end{matrix} \right| = \left|\begin{matrix} g_{11} & g_{13} \\ g_{31} & g_{33} \end{matrix} \right|\displaystyle M_{23} = \left|\begin{matrix} g_{11} & g_{12} & \bold{g_{13}} \\ \bold{g_{21}} & \bold{g_{22}} & \bold{g_{23}} \\ g_{31} & g_{32} & \bold{g_{33}} \end{matrix} \right| = \left|\begin{matrix} g_{11} & g_{12} \\ g_{31} & g_{32} \end{matrix} \right|
\displaystyle M_{31} = \left|\begin{matrix} \bold{g_{11}} & g_{12} & g_{13} \\ \bold{g_{21}} & g_{22} & g_{23} \\ \bold{g_{31}} & \bold{g_{32}} & \bold{g_{33}} \end{matrix} \right| = \left|\begin{matrix} g_{12} & g_{13} \\ g_{22} & g_{23} \end{matrix} \right|\displaystyle M_{32} = \left|\begin{matrix} g_{11} & \bold{g_{12}} & g_{13} \\ g_{21} & \bold{g_{22}} & g_{23} \\ \bold{g_{31}} & \bold{g_{32}} & \bold{g_{33}} \end{matrix} \right| = \left|\begin{matrix} g_{11} & g_{13} \\ g_{21} & g_{23} \end{matrix} \right|\displaystyle M_{33} = \left|\begin{matrix} g_{11} & g_{12} & \bold{g_{13}} \\ g_{21} & g_{22} & \bold{g_{23}} \\ \bold{g_{31}} & \bold{g_{32}} & \bold{g_{33}} \end{matrix} \right| = \left|\begin{matrix} g_{11} & g_{12} \\ g_{21} & g_{22} \end{matrix} \right|

Teniendo los resultados de cada menor, se puede calcular cada cofactor

\displaystyle C_{11} = {(-1)}^{1+1} M_{11} = M_{11}\displaystyle C_{12} = {(-1)}^{1+2} M_{12} = - M_{12}\displaystyle C_{13} = {(-1)}^{1+3} M_{13} = M_{13}
\displaystyle C_{21} = {(-1)}^{2+1} M_{21} = - M_{21}\displaystyle C_{22} = {(-1)}^{2+2} M_{22} = M_{22}\displaystyle C_{23} = {(-1)}^{2+3} M_{23} = - M_{23}
\displaystyle C_{31} = {(-1)}^{3+1} M_{31} = M_{31}\displaystyle C_{32} = {(-1)}^{3+2} M_{32} = - M_{32}\displaystyle C_{33} = {(-1)}^{3+3} M_{33} = M_{33}

Nota. El determinante de cada menor no fue desarrollado ya que genera varios términos; sólo se expresará cuando se resuelva un problema donde implique matrices de 3×3.

Así, ya es posible conocer el resultado de la matriz adjunta de \bold{G}

\displaystyle Adj \ \bold{G} = \left[\begin{matrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{matrix} \right] = \left[\begin{matrix} M_{11} & - M_{12} & M_{13} \\ - M_{21} & M_{22} &- M_{23} \\ M_{31} & - M_{32} & M_{33} \end{matrix} \right]

Una vez calculada la matriz adjunta, puede determinarse su traspuesta.

\displaystyle {(Adj \ \bold{G})}^T = \left[\begin{matrix} M_{11} & - M_{21} & M_{31} \\ - M_{12} & M_{22} &- M_{32} \\ M_{13} & - M_{23} & M_{33} \end{matrix} \right]

Una vez calculado el determinante y la matriz adjunta traspuesta de \bold{G}, se puede determinar la inversa de \bold{G}. Posteriormente, realizando la multiplicación matricial, es posible encontrar los valores de las incógnitas v_1, v_2 y v_3.

\displaystyle \bold{V} = \bold{G}^{-1} \bold{I}

\displaystyle \left[\begin{matrix} v_1 \\ v_2 \\ v_3 \end{matrix} \right] = \frac{{(Adj \ \bold{G})}^T}{\text{det} \ \bold{G}} \left[\begin{matrix} i_1 \\ i_2 \\ i_3 \end{matrix} \right] = \left(\frac{1}{\text{det} \ \bold{G}} \right) {(Adj \ \bold{G})}^T \left[\begin{matrix} i_1 \\ i_2 \\ i_3 \end{matrix} \right]

\displaystyle \left[\begin{matrix} v_1 \\ v_2 \\ v_3 \end{matrix} \right] = \frac{1}{\left(g_{11} g_{22} g_{33} + g_{12} g_{23} g_{31} + g_{13} g_{21} g_{32} \right) - \left(g_{31} g_{22} g_{13} + g_{32} g_{23} g_{11} + g_{33} g_{21} g_{12} \right)} \left[\begin{matrix} M_{11} & - M_{21} & M_{31} \\ - M_{12} & M_{22} &- M_{32} \\ M_{13} & - M_{23} & M_{33} \end{matrix} \right] \left[\begin{matrix} i_1 \\ i_2 \\ i_3 \end{matrix} \right]

Problema resuelto

Problema 1. En la red de la figura 5, dados los valores siguientes, determine los voltajes de nodo: R_1 = R_2 = 2 \ \text{k} \Omega, R_3 = R_4 = 4 \ \text{k} \Omega, R_5 = 1 \ \text{k} \Omega, i_A = 4 \ \text{mA} e i_B = 2 \ \text{mA}.

Figura 5. Circuito del problema 1.

Aplicando la LKC en el nodo 1, se tiene

\displaystyle \sum_{j=1}^{n}{i_j} = 0

\displaystyle \frac{v_1}{R_2} + \frac{v_1 - v_3}{R_1} + i_A = 0

\displaystyle \frac{v_1}{R_2} + \frac{v_1}{R_1} - \frac{v_3}{R_1} + i_A = 0

\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_2} \right) v_1 - \left(\frac{1}{R_1} \right) v_3 = - i_A

Figura 6. Señalando el nodo 1 para el análisis por LKC.

Usando la LKC para el nodo 2, se tiene que

\displaystyle \sum_{j=1}^{n}{i_j} = 0

\displaystyle -i_A + \frac{v_2}{R_3} + i_B + \frac{v_2 - v_3}{R_4} = 0

\displaystyle \left(\frac{1}{R_3} + \frac{1}{R_4} \right) v_2 - \left(\frac{1}{R_4}\right) v_3 = i_A - i_B

Figura 7. Señalando el nodo 2 para el análisis por LKC.

Haciendo el mismo procedimiento para el nodo 3,

\displaystyle \sum_{j=1}^{n}{i_j} = 0

\displaystyle \frac{v_3}{R_5} + \frac{v_3-v_2}{R_4} + \frac{v_3 - v_1}{R_1} = 0

\displaystyle - \left(\frac{1}{R_1} \right) v_1 - \left(\frac{1}{R_4} \right) v_2 + \left(\frac{1}{R_1} + \frac{1}{R_4} + \frac{1}{R_5} \right) v_3 = 0

Figura 8. Señalando el nodo 3 para el análisis por LKC.

Entonces, el conjunto de ecuaciones son

\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_2} \right) v_1 - \left(\frac{1}{R_1} \right) v_3 = - i_A
\displaystyle \left(\frac{1}{R_3} + \frac{1}{R_4} \right) v_2 - \left(\frac{1}{R_4}\right) v_3 = i_A - i_B
\displaystyle - \left(\frac{1}{R_1} \right) v_1 - \left(\frac{1}{R_4} \right) v_2 + \left(\frac{1}{R_1} + \frac{1}{R_4} + \frac{1}{R_5} \right) v_3 = 0

Recordando que R_1 = R_2 = 2 \ \text{k} \Omega, R_3 = R_4 = 4 \ \text{k} \Omega, R_5 = 1 \ \text{k} \Omega, i_A = 4 \ \text{mA} e i_B = 2 \ \text{mA}, al sustituir resulta

\displaystyle \left(\frac{1}{2 \ \text{k}} + \frac{1}{2 \ \text{k}} \right) v_1 - \left(\frac{1}{2 \ \text{k}} \right) v_3 = - 4 \ \text{m}
\displaystyle \left(\frac{1}{4 \ \text{k}} + \frac{1}{4 \ \text{k}} \right) v_2 - \left(\frac{1}{4 \ \text{k}}\right) v_3 = 4 \ \text{m} - 2 \ \text{m}
\displaystyle - \left(\frac{1}{2 \ \text{k}} \right) v_1 - \left(\frac{1}{4 \ \text{k}} \right) v_2 + \left(\frac{1}{2 \ \text{k}} + \frac{1}{4 \ \text{k}} + \frac{1}{1 \ \text{k}} \right) v_3 = 0

Reduciendo

\displaystyle \left(\frac{1}{1 \ \text{k}} \right) v_1 - \left(\frac{1}{2 \ \text{k}} \right) v_3 = - 4 \ \text{m}
\displaystyle \left(\frac{1}{2 \ \text{k}} \right) v_2 - \left(\frac{1}{4 \ \text{k}}\right) v_3 = 2 \ \text{m}
\displaystyle - \left(\frac{1}{2 \ \text{k}} \right) v_1 - \left(\frac{1}{4 \ \text{k}} \right) v_2 + \left(\frac{7}{4 \ \text{k}} \right) v_3 = 0

Ahora, este sistema se puede expresar en forma matricial

\displaystyle \left[ \begin{matrix} \frac{1}{1 \ \text{k}} & 0 & - \frac{1}{2 \ \text{k}} \\ \\ 0 & \frac{1}{2 \ \text{k}} & - \frac{1}{4 \ \text{k}} \\ \\ - \frac{1}{2 \ \text{k}} & - \frac{1}{4 \ \text{k}} & \frac{7}{4 \ \text{k}} \end{matrix} \right] \left[ \begin{matrix} v_1 \\ v_2 \\ v_3 \end{matrix} \right] = \left[ \begin{matrix} -4 \ \text{m} \\ 2 \ \text{m} \\ 0 \end{matrix} \right]

y esto es idéntico a

\displaystyle \bold{G} \bold{V} = \bold{I}

donde

\displaystyle \bold{G} = \left[ \begin{matrix} \frac{1}{1 \ \text{k}} & 0 & - \frac{1}{2 \ \text{k}} \\ \\ 0 & \frac{1}{2 \ \text{k}} & - \frac{1}{4 \ \text{k}} \\ \\ - \frac{1}{2 \ \text{k}} & - \frac{1}{4 \ \text{k}} & \frac{7}{4 \ \text{k}} \end{matrix} \right]

Para poder llegar a \displaystyle \bold{V} = \bold{G}^{-1} \bold{I}, es necesario hallar la inversa de \bold{G}. Así que, primero se calcula el determinante de \bold{G}

\displaystyle \text{det} \ \bold{G} = |\bold{G}|

\displaystyle \text{det} \ \bold{G} = \left| \begin{matrix} \frac{1}{1 \ \text{k}} & 0 & - \frac{1}{2 \ \text{k}}\\ \\ 0 & \frac{1}{2 \ \text{k}} & - \frac{1}{4 \ \text{k}} \\ \\ - \frac{1}{2 \ \text{k}} & - \frac{1}{4 \ \text{k}} & \frac{7}{4 \ \text{k}} \end{matrix} \right|

\displaystyle \text{det} \ \bold{G} = \left| \begin{matrix} \frac{1}{1 \ \text{k}} & 0 & - \frac{1}{2 \ \text{k}}\\ \\ 0 & \frac{1}{2 \ \text{k}} & - \frac{1}{4 \ \text{k}} \\ \\ - \frac{1}{2 \ \text{k}} & - \frac{1}{4 \ \text{k}} & \frac{7}{4 \ \text{k}} \end{matrix} \right| \quad \begin{matrix} \frac{1}{1 \ \text{k}} & 0 \\ \\ 0 & \frac{1}{2 \ \text{k}} \\ \\ - \frac{1}{2 \ \text{k}} & - \frac{1}{4 \ \text{k}} \end{matrix}

\displaystyle \text{det} \ \bold{G} = \left[ \left(\frac{1}{1 \ \text{k}} \right) \left(\frac{1}{2 \ \text{k}} \right) \left(\frac{7}{4 \ \text{k}} \right) + \left(0 \right) \left(- \frac{1}{4 \ \text{k}}\right) \left(- \frac{1}{2 \ \text{k}} \right) + \left(-\frac{1}{2 \ \text{k}} \right) \left( 0 \right) \left(-\frac{1}{4 \ \text{k}} \right) \right] - \left[\left(-\frac{1}{2 \ \text{k}} \right) \left(\frac{1}{2 \ \text{k}} \right) \left(-\frac{1}{2 \ \text{k}} \right) + \left(-\frac{1}{4 \ \text{k}} \right) \left(-\frac{1}{4 \ \text{k}} \right) \left(\frac{1}{1 \ \text{k}} \right) + \left(\frac{7}{4 \ \text{k}} \right) \left(0 \right) \left(0 \right) \right]

\displaystyle \text{det} \ \bold{G} = \left( \frac{7}{8 \ \text{k}^3} + 0 + 0 \right) - \left(\frac{1}{8 \ \text{k}^3} +\frac{1}{16 \ \text{k}^3} + 0 \right) = \left( \frac{7}{8 \ \text{k}^3} \right) - \left(\frac{2}{16 \ \text{k}^3} +\frac{1}{16 \ \text{k}^3} \right)

\displaystyle \text{det} \ \bold{G} = \left( \frac{7}{8 \ \text{k}^3} \right) - \left(\frac{3}{16 \ \text{k}^3} \right)= \frac{7}{8 \ \text{k}^3} - \frac{3}{16 \ \text{k}^3} = \frac{14}{16 \ \text{k}^3} - \frac{3}{16 \ \text{k}^3}

\displaystyle \text{det} \ \bold{G} = \frac{11}{16 \ \text{k}^3}

Para calcular la matriz adjunta de \bold{G}

\displaystyle Adj \ \bold{G} = \left[\begin{matrix} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{matrix} \right]

es necesario calcular los menores (que pertenecen a cada cofactor).

\displaystyle M_{11} = \left|\begin{matrix} \frac{1}{2 \ \text{k}} & - \frac{1}{4 \ \text{k}} \\ \\ -\frac{1}{4 \ \text{k}} & \frac{7}{4 \ \text{k}} \end{matrix} \right| = \frac{13}{16 \ \text{k}^2}\displaystyle M_{12} = \left|\begin{matrix} 0 & - \frac{1}{4 \ \text{k}} \\ \\ - \frac{1}{2 \ \text{k}} & \frac{7}{4 \ \text{k}} \end{matrix} \right| = -\frac{1}{8 \ \text{k}^2}\displaystyle M_{13} = \left|\begin{matrix} 0 & \frac{1}{2 \ \text{k}} \\ \\ - \frac{1}{2 \ \text{k}} & - \frac{1}{4 \ \text{k}} \end{matrix} \right| = \frac{1}{4 \ \text{k}^2}
\displaystyle M_{21} = \left|\begin{matrix} 0 & - \frac{1}{2 \ \text{k}} \\ \\ - \frac{1}{4 \ \text{k}} & \frac{7}{4 \ \text{k}} \end{matrix} \right| = -\frac{1}{8 \ \text{k}^2}\displaystyle M_{22} = \left|\begin{matrix} \frac{1}{1 \ \text{k}} & - \frac{1}{2 \ \text{k}} \\ \\ - \frac{1}{2 \ \text{k}} & \frac{7}{4 \ \text{k}} \end{matrix} \right| = \frac{3}{2 \ \text{k}^2}\displaystyle M_{23} = \left|\begin{matrix} \frac{1}{1 \ \text{k}} & 0 \\ \\ - \frac{1}{2 \ \text{k}} & - \frac{1}{4 \ \text{k}} \end{matrix} \right| = -\frac{1}{4 \ \text{k}^2}
\displaystyle M_{31} = \left|\begin{matrix} 0 & - \frac{1}{2 \ \text{k}} \\ \\ \frac{1}{2 \ \text{k}} & - \frac{1}{4 \ \text{k}} \end{matrix} \right| = \frac{1}{4 \ \text{k}^2}\displaystyle M_{32} = \left|\begin{matrix} \frac{1}{1 \ \text{k}} & - \frac{1}{2 \ \text{k}} \\ \\ 0 & -\frac{1}{4 \ \text{k}} \end{matrix} \right| = -\frac{1}{4 \ \text{k}^2}\displaystyle M_{33} = \left|\begin{matrix} \frac{1}{1 \ \text{k}} & 0 \\ \\ 0 & \frac{1}{2 \ \text{k}} \end{matrix} \right| = \frac{1}{2 \ \text{k}^2}

Entonces, los cofactores tiene los siguientes valores

\displaystyle C_{11} = M_{11} = \frac{13}{16 \ \text{k}^2}\displaystyle C_{12} = - M_{12} = - \left(-\frac{1}{8 \ \text{k}^2} \right) = \frac{1}{8 \ \text{k}^2}\displaystyle C_{13} = M_{13} = \frac{1}{4 \ \text{k}^2}
\displaystyle C_{21} = - M_{21} = - \left(-\frac{1}{8 \ \text{k}^2} \right) = \frac{1}{8 \ \text{k}^2}\displaystyle C_{22} = M_{22} = \frac{3}{2 \ \text{k}^2}\displaystyle C_{23} = - M_{23} = - \left(-\frac{1}{4 \ \text{k}^2} \right) = \frac{1}{4 \ \text{k}^2}
\displaystyle C_{31} = M_{31} = \frac{1}{4 \ \text{k}^2}\displaystyle C_{32} = - M_{32} = -\left(-\frac{1}{4 \ \text{k}^2} \right) = \frac{1}{4 \ \text{k}^2}\displaystyle C_{33} = M_{33} = \frac{1}{2 \ \text{k}^2}

La matriz adjunta de \bold{G} esperada es

\displaystyle Adj \ \bold{G} = \left[\begin{matrix} \frac{13}{16 \ \text{k}^2} & \frac{1}{8 \ \text{k}^2} & \frac{1}{4 \ \text{k}^2} \\ \\ \frac{1}{8 \ \text{k}^2} & \frac{3}{2 \ \text{k}^2} & \frac{1}{4 \ \text{k}^2} \\ \\ \frac{1}{4 \ \text{k}^2} & \frac{1}{4 \ \text{k}^2} & \frac{1}{2 \ \text{k}^2} \end{matrix} \right]

La matriz adjunta traspuesta de \bold{G} es

\displaystyle {(Adj \ \bold{G})}^T = \left[\begin{matrix} \frac{13}{16 \ \text{k}^2} & \frac{1}{8 \ \text{k}^2} & \frac{1}{4 \ \text{k}^2} \\ \\ \frac{1}{8 \ \text{k}^2} & \frac{3}{2 \ \text{k}^2} & \frac{1}{4 \ \text{k}^2} \\ \\ \frac{1}{4 \ \text{k}^2} & \frac{1}{4 \ \text{k}^2} & \frac{1}{2 \ \text{k}^2} \end{matrix} \right]

Calculando la matriz inversa

\displaystyle \bold{G}^{-1} = \left(\frac{1}{\text{det} \ \bold{G}} \right) {(Adj \ \bold{G})}^T

\displaystyle \bold{G}^{-1} = \frac{1}{\frac{11}{16 \ \text{k}^3}} \left[\begin{matrix} \frac{13}{16 \ \text{k}^2} & \frac{1}{8 \ \text{k}^2} & \frac{1}{4 \ \text{k}^2} \\ \\ \frac{1}{8 \ \text{k}^2} & \frac{3}{2 \ \text{k}^2} & \frac{1}{4 \ \text{k}^2} \\ \\ \frac{1}{4 \ \text{k}^2} & \frac{1}{4 \ \text{k}^2} & \frac{1}{2 \ \text{k}^2} \end{matrix} \right] = \frac{16 \ \text{k}^3}{11} \left[\begin{matrix} \frac{13}{16 \ \text{k}^2} & \frac{1}{8 \ \text{k}^2} & \frac{1}{4 \ \text{k}^2} \\ \\ \frac{1}{8 \ \text{k}^2} & \frac{3}{2 \ \text{k}^2} & \frac{1}{4 \ \text{k}^2} \\ \\ \frac{1}{4 \ \text{k}^2} & \frac{1}{4 \ \text{k}^2} & \frac{1}{2 \ \text{k}^2} \end{matrix} \right]

\displaystyle \bold{G}^{-1} = \left[\begin{matrix} \frac{16 \ \text{k}^3}{11} \left(\frac{13}{16 \ \text{k}^2} \right) & \frac{16 \ \text{k}^3}{11} \left(\frac{1}{8 \ \text{k}^2} \right) & \frac{16 \ \text{k}^3}{11} \left(\frac{1}{4 \ \text{k}^2} \right) \\ \\ \frac{16 \ \text{k}^3}{11} \left(\frac{1}{8 \ \text{k}^2} \right) & \frac{16 \ \text{k}^3}{11} \left(\frac{3}{2 \ \text{k}^2} \right) & \frac{16 \ \text{k}^3}{11} \left(\frac{1}{4 \ \text{k}^2} \right) \\ \\ \frac{16 \ \text{k}^3}{11} \left(\frac{1}{4 \ \text{k}^2} \right) & \frac{16 \ \text{k}^3}{11} \left(\frac{1}{4 \ \text{k}^2} \right) & \frac{16 \ \text{k}^3}{11} \left(\frac{1}{2 \ \text{k}^2} \right) \end{matrix} \right]

\displaystyle \bold{G}^{-1} = \left[\begin{matrix} \frac{208}{176} \text{k} & \frac{16}{88} \text{k} & \frac{16}{44} \text{k} \\ \\ \frac{16}{88} \text{k} & \frac{48}{22} \text{k} & \frac{16}{44} \text{k} \\ \\ \frac{16}{44} \text{k} & \frac{16}{44} \text{k} & \frac{16}{22} \text{k} \end{matrix} \right] = \left[\begin{matrix} \frac{13}{11} \text{k} & \frac{2}{11} \text{k} & \frac{4}{11} \text{k} \\ \\ \frac{2}{11} \text{k} & \frac{24}{11} \text{k} & \frac{4}{11} \text{k} \\ \\ \frac{4}{11} \text{k} & \frac{4}{11} \text{k} & \frac{8}{11} \text{k} \end{matrix} \right]

Entonces, la forma matricial desarrollada es

\displaystyle \bold{V} = \bold{G}^{-1} \bold{I}

\displaystyle \left[\begin{matrix} v_1 \\ v_2 \\ v_3 \end{matrix} \right] = \left[\begin{matrix} \frac{13}{11} \text{k} & \frac{2}{11} \text{k} & \frac{4}{11} \text{k} \\ \\ \frac{2}{11} \text{k} & \frac{24}{11} \text{k} & \frac{4}{11} \text{k} \\ \\ \frac{4}{11} \text{k} & \frac{4}{11} \text{k} & \frac{8}{11} \text{k} \end{matrix} \right] \left[ \begin{matrix} -4 \ \text{m} \\ 2 \ \text{m} \\ 0 \end{matrix} \right]

Realizando la multiplicación matricial en el segundo miembro, resulta

\displaystyle \left[\begin{matrix} v_1 \\ v_2 \\ v_3 \end{matrix} \right] = \left[\begin{matrix} \left(\frac{13}{11} \text{k} \right) (-4 \ \text{m}) + \left(\frac{2}{11} \text{k} \right) (2 \ \text{m}) + \left(\frac{4}{11} \text{k} \right) (0) \\ \\ \left(\frac{2}{11} \text{k} \right) (-4 \ \text{m}) + \left(\frac{24}{11} \text{k} \right) (2 \ \text{m}) + \left(\frac{4}{11} \text{k} \right) (0) \\ \\ \left(\frac{4}{11} \text{k} \right)(-4 \ \text{m}) + \left(\frac{4}{11} \text{k} \right)(2 \ \text{m}) + \left(\frac{8}{11} \text{k} \right) (0) \end{matrix} \right]

recordando que \text{m} = 1 \times 10^{-3} y \text{k} = 1 \times 10^3, resulta

\displaystyle \left[\begin{matrix} v_1 \\ v_2 \\ v_3 \end{matrix} \right] = \left[\begin{matrix} \left(\frac{13}{11} \times 10^3 \right) (-4 \times 10^{-3}) + \left(\frac{2}{11} \times 10^{3} \right) (2 \times 10^{-3}) + \left(\frac{4}{11} \times 10^{3} \right) (0) \\ \\ \left(\frac{2}{11} \times 10^{3} \right) (-4 \times 10^{-3}) + \left(\frac{24}{11} \times 10^{3} \right) (2 \times 10^{-3}) + \left(\frac{4}{11} \times 10^{3} \right) (0) \\ \\ \left(\frac{4}{11} \times 10^{3} \right)(-4 \times 10^{-3}) + \left(\frac{4}{11} \times 10^{3} \right)(2 \times 10^{-3}) + \left(\frac{8}{11} \times 10^{3} \right) (0) \end{matrix} \right]

\displaystyle \left[\begin{matrix} v_1 \\ v_2 \\ v_3 \end{matrix} \right] = \left[\begin{matrix} -\frac{52}{11} + \frac{4}{11} + 0 \\ \\ -\frac{8}{11} + \frac{48}{11} + 0 \\ \\ - \frac{16}{11} + \frac{8}{11} + 0 \end{matrix} \right] = \left[\begin{matrix} - \frac{48}{11} \\ \\ \frac{40}{11} \\ \\ - \frac{8}{11} \end{matrix} \right]

\displaystyle \therefore \left[\begin{matrix} v_1 \\ v_2 \\ v_3 \end{matrix} \right] = \left[\begin{matrix} -4.3636 \\ \\ 3.6364 \\ \\ - 0.7273 \end{matrix} \right] \ \text{V}

Se concluye que los voltajes de cada nodo son v_1 = -4.3636 \ \text{V}, v_2 = 3.6364 \ \text{V} y v_3 = -0.7273 \ \text{V}.

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.