Cálculo de la integral definida utilizando el cambio de límites correspondiente a un cambio de la variable. Cálculo integral.

Introducción

Cuando se integra por sustitución de una variable (método de integración por racionalización), a veces es algo laborioso retransformar el resultado en función de la variable primitiva. Sin embargo, cuando se integra entre límites se puede evitar el procedimiento de reponer la variable primitiva, cambiando los límites de tal manera que correspondan a la nueva variable.

Problemas resueltos

Problema 1. Hallar la $\displaystyle \int_0^{16}{\frac{x^{\frac{1}{2}} \, dx}{1+x^{\frac{3}{4}}}}$ .

Solución. Por el método de integración por racionalización, se observa que la potencia del radical (ubicado en el denominador), $\displaystyle n=4$ , entonces $x=z^n=z^4$ . Además, $\displaystyle x^{\frac{1}{2}}=z^2$ , $\displaystyle x^{\frac{3}{4}}=z^3$ y $dx=4z^3 \, dz$ . Cambiando los límites, se observa que cuando $x=0$ , $z=0$ , y cuando $x=16$ , $z=2$ . Así que

$\displaystyle \int_0^{16}{\frac{x^{\frac{1}{2}} \, dx}{1+x^{\frac{3}{4}}}} = \int_0^2{\frac{z^2 \cdot 4z^3 \, dz}{1 + z^3}} = 4 \int_0^2{\frac{z^5}{1+z^3} \, dz}$

Después, se resuelve la integral definida como una integral indefinida.

$\displaystyle \int_0^2{\frac{z^5}{1+z^3} \, dz} \quad \rightarrow \quad \int{\frac{z^5}{1+z^3} \, dz}$

Como el numerador tiene mayor potencia que en el denominador, se realiza una división.

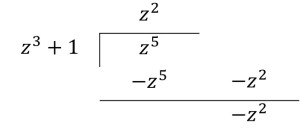
Por tanto, el resultado de esta división es

$\displaystyle \frac{z^5}{1+z^3} = z^2 - \frac{z^2}{1+z^3}$

Continuando

$\displaystyle \int{\frac{z^5}{1+z^3} \, dz} = \int{\left(z^2 - \frac{z^2}{1+z^3} \right) \, dz}$

$\displaystyle \int{\frac{z^5}{1+z^3} \, dz} = \underbrace{\int{z^2 \, dz}}_{1} - \underbrace{\int{\frac{z^2 \, dz}{1+z^3}}}_{2}$

La primera integral es similar a

$\displaystyle \int{v^n \, dv} = \frac{1}{n+1} v^{n+1} + C$

Entonces

$\displaystyle \int{z^2 \, dz} = \frac{1}{2+1} z^{2+1} + C = \frac{1}{3} z^3 + C$

La segunda integral es similar a

$\displaystyle \int{\frac{dv}{v}} = \ln{v} + C$

Analizando la variable $v$

\displaystyle dv = 3z^2 dz \quad \rightarrow \quad z^2 dz = \frac{1}{3} \, dv

Su resultado es

$\displaystyle \int{\frac{z^2 \, dz}{1+z^3}} = \int{\frac{\frac{1}{3} dv}{v}}$

$\displaystyle \int{\frac{z^2 \, dz}{1+z^3}} = \frac{1}{3} \int{\frac{dv}{v}} = \frac{1}{3} [\ln{v} + C] = \frac{1}{3} \ln{v} + C$

$\displaystyle \int{\frac{z^2 \, dz}{1+z^3}} = \frac{1}{3} \ln{(1+z^3)} + C$

Sustituyendo los resultados obtenidos, se tiene que

$\displaystyle \int{\frac{z^5}{1+z^3} \, dz} = \int{z^2 \, dz} - \int{\frac{z^2 \, dz}{1+z^3}}$

$\displaystyle \int{\frac{z^5}{1+z^3} \, dz} = \frac{1}{3} z^3 - \frac{1}{3} \ln{(1+z^3)} + C$

Reemplazando la variable por los límites, resulta

$\displaystyle \int_0^2{\frac{z^5}{1+z^3} \, dz} = \left[\frac{1}{3} z^3 - \frac{1}{3} \ln{(1+z^3)} + C \right]_0^2$

$\displaystyle \int_0^2{\frac{z^5}{1+z^3} \, dz} = \left[\frac{1}{3} {(2)}^3 - \frac{1}{3} \ln{(1+2^3)} \right] -\left[\frac{1}{3} {(0)}^3 - \frac{1}{3} \ln{(1+0^3)} \right]$

$\displaystyle \int_0^2{\frac{z^5}{1+z^3} \, dz} = \left(\frac{8}{3} - \frac{1}{3} \ln{9} \right) - \left(0 - \frac{1}{3} \ln{1} \right)$

$\displaystyle \int_0^2{\frac{z^5}{1+z^3} \, dz} = 1.934$

Regresando

$\displaystyle \int_0^{16}{\frac{x^{\frac{1}{2}} \, dx}{1+x^{\frac{3}{4}}}} = 4 \int_0^2{\frac{z^5}{1+z^3} \, dz}$

$\displaystyle \int_0^{16}{\frac{x^{\frac{1}{2}} \, dx}{1 + x^{\frac{3}{4}}}} = 4 (1.934)$

$\displaystyle \int_0^{16}{\frac{x^{\frac{1}{2}} \, dx}{1 + x^{\frac{3}{4}}}} = 7.736$

Finalmente

$\displaystyle \therefore \int_0^{16}{\frac{x^{\frac{1}{2}} \, dx}{1+x^{\frac{3}{4}}}} = 7.736$

Problema 2. Hallar $\displaystyle \int_3^{29}{\frac{(x-2)^{\frac{2}{3}} \, dx}{(x-2)^{\frac{2}{3}} + 3}}$ .

Solución. Aplicando el método de integración por racionalización, se observa que $n=3$ , es decir, $(x-2)=z^3$ . Además, $\displaystyle (x-2)^{\frac{2}{3}}=z^2$ y $dx=3z^2 \, dz$ . Para cambiar los límites, se observa que cuando $x=3$ , $z=1$ , y cuando $x=29$ , $z=3$ . Entonces

$\displaystyle \int_3^{29}{\frac{(x-2)^{\frac{2}{3}} \, dx}{(x-2)^{\frac{2}{3}} + 3}} = \int_1^3{\frac{z^2 \cdot 3z^2 \, dz}{z^2+3}} = 3 \int_1^3{\frac{z^4}{z^2+3} \, dz}$

Después, se resuelve la integral definida como una integral indefinida.

$\displaystyle \int_1^3{\frac{z^4}{z^2+3} \, dz} \quad \rightarrow \quad \int{\frac{z^4}{z^2+3} \, dz}$

El numerador de la fracción racional tiene una potencia mayor que la del denominador, entonces, se realiza una división.

Por tanto, el resultado de esta división es

$\displaystyle \frac{z^4}{z^2+3} = z^2 - 3 + \frac{9}{z^2+3}$

Entonces

$\displaystyle \int{\frac{z^4}{z^2+3}} = \int{\left(z^2 - 3 + \frac{9}{z^2+3} \right) \ dz}$

$\displaystyle \int{\frac{z^4}{z^2+3}} = \underbrace{\int{z^2 \, dz}}_{1} - 3 \underbrace{\int{dz}}_{2} + 9 \underbrace{\int{\frac{dz}{z^2+3}}}_{3}$

La primera integral es similar a

$\displaystyle \int{v^n \, dv} = \frac{1}{n+1} v^{n+1} + C$

Su resultado es

$\displaystyle \int{z^2 \, dz} = \frac{1}{2+1} z^{2+1} + C = \frac{1}{3} z^3 + C$

La segunda integral es similar a

$\displaystyle \int{dv} = v + C$

Su resultado es

$\displaystyle \int{dz} = z+C$

La tercera integral es similar a

$\displaystyle \int{\frac{dv}{v^2+a^2}} = \frac{1}{a} \arctan{(\frac{v}{a})} + C$

donde

Su resultado es

$\displaystyle \int{\frac{dz}{z^2+3}} = \frac{1}{\sqrt{3}} \arctan{\left(\frac{z}{\sqrt{3}} \right)} + C$

Sustituyendo los resultados obtenidos, se tiene que

$\displaystyle \int{\frac{z^4}{z^2+3}} = \int{z^2 \, dz} - 3 \int{dz} + 9 \int{\frac{dz}{z^2+3}}$

$\displaystyle \int{\frac{z^4}{z^2+3}} = \frac{1}{3} z^3 - 3 (z) + 9 \left[\frac{1}{\sqrt{3}} \arctan{\left(\frac{z}{\sqrt{3}} \right)} \right] + C$

$\displaystyle \int{\frac{z^4}{z^2+3}} = \frac{1}{3} z^3 - 3z + \frac{9}{\sqrt{3}} \arctan{\left(\frac{z}{\sqrt{3}} \right)} + C$

$\displaystyle \int{\frac{z^4}{z^2+3}} = \frac{1}{3} z^3 - 3z + 3 \sqrt{3} \arctan{\left(\frac{z}{\sqrt{3}} \right)} + C$

Reemplazando la variable por los límites, resulta

$\displaystyle \int_1^3{\frac{z^4}{z^2+3}} = \left[\frac{1}{3} z^3 - 3z + 3 \sqrt{3} \arctan{\left(\frac{z}{\sqrt{3}} \right)} + C \right]_1^3$

$\displaystyle \int_1^3{\frac{z^4}{z^2+3}} = \left[\frac{1}{3} (3)^3 - 3(3) + 3 \sqrt{3} \arctan{\left(\frac{3}{\sqrt{3}} \right)} \right] - \left[\frac{1}{3} (1)^3 - 3(1) + 3 \sqrt{3} \arctan{\left(\frac{1}{\sqrt{3}} \right)} \right]$

$\displaystyle \int_1^3{\frac{z^4}{z^2+3}} = \left[9 - 9 + 3 \sqrt{3} \left(\frac{\pi}{3} \right) \right] - \left[\frac{1}{3} - 3 + 3 \sqrt{3} \left(\frac{\pi}{6} \right) \right]$

$\displaystyle \int_1^3{\frac{z^4}{z^2+3}} = (\sqrt{3} \pi) - \left(-\frac{8}{3} + \frac{\sqrt{3}}{2} \pi \right)$

$\displaystyle \int_1^3{\frac{z^4}{z^2+3}} = \sqrt{3} \pi +\frac{8}{3} - \frac{\sqrt{3}}{2} \pi$

$\displaystyle \int_1^3{\frac{z^4}{z^2+3}} = \frac{8}{3} + \frac{\sqrt{3}}{2} \pi$

Regresando

$\displaystyle \int_3^{29}{\frac{(x-2)^{\frac{2}{3}} \, dx}{(x-2)^{\frac{2}{3}} + 3}} = 3 \int_1^3{\frac{z^4}{z^2+3} \, dz}$

$\displaystyle \int_3^{29}{\frac{(x-2)^{\frac{2}{3}} \, dx}{(x-2)^{\frac{2}{3}} + 3}} = 3 \left(\frac{8}{3} + \frac{\sqrt{3}}{2} \pi \right)$

$\displaystyle \int_3^{29}{\frac{(x-2)^{\frac{2}{3}} \, dx}{(x-2)^{\frac{2}{3}} + 3}} = 8 + \frac{3\sqrt{3}}{2} \pi$

Finalmente

$\displaystyle \therefore \int_3^{29}{\frac{(x-2)^{\frac{2}{3}} \, dx}{(x-2)^{\frac{2}{3}} + 3}} = 8 + \frac{3\sqrt{3}}{2} \pi \approx 16.162$

$v^2 = z^2$	$a^2 = 3$
$v = z$	$\displaystyle a = \sqrt{3}$
$dv = dz$

Cálculo de la integral definida utilizando el cambio de límites correspondiente a un cambio de la variable. Cálculo integral.

Introducción

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Cálculo de la integral definida utilizando el cambio de límites correspondiente a un cambio de la variable. Cálculo integral.

Introducción

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta