Introducción

Por lo general, las coordenadas x y y de algún punto en una curva se pueden expresar en funciones de una tercera variable, por ejemplo t o \theta, la cual se denomina parámetro. Las ecuaciones de la curva x=f(t) y y = \phi (t) están expresadas de forma paramétrica, y en donde cada valor que se le asigna a t brinda un valor de x y un valor de y, y esto da un lugar a un punto de la curva.

Entonces

x=f(t) \quad \quad \quad y=\phi (t)

Calculando la diferencial de la variable x

\displaystyle \frac{dx}{dt} = \frac{d}{dt} [f(t)]

\displaystyle \frac{dx}{dt} = f'(t)

\displaystyle dx = f' (t) \ dt

Tomando la fórmula para determinar el área

\displaystyle \text{Area} = \int_a^b{y \, dx}

\displaystyle \text{Area} = \int_{t_1}^{t_2}{\phi (t) f' (t) \, dt}

Se observa que los límites ahora son t=t_1 cuando x=a y t=t_2 cuando x=b.

Si la curva tuviera ecuaciones paramétricas con términos de \theta, el área a calcular sería

\displaystyle \text{Area} = \int_{\theta_1}^{\theta_2}{\phi (\theta) f' (\theta) \, d\theta}

Se observa que los límites ahora son \theta = \theta_1 cuando x=a y \theta = \theta_2 cuando x=b.

Problemas resueltos

Problema 1. Hallar el área de la superficie limitada por una arcada de la cicloide x = a(\theta - \sin{\theta}), y = a(1 - \cos{\theta}) y el eje de las x.

Solución. Se realiza una tabulación mediante las ecuaciones de la cicloide desde 0 hasta 2\pi (donde se ha considerado el valor de a=1 para llevar a cabo sólo la tabulación).

valores4

Graficando la función

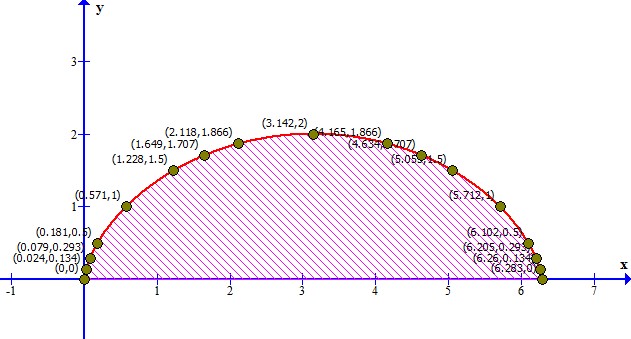
figura 4.2.6
Figura 6. Representación gráfica de las ecuaciones x = a(θ – sen θ), y = a(1 – cos θ).

Entonces, los límites de la arcada son \theta=0 y \theta=2\pi. Determinando la primera derivada para la ecuación x, se tiene

x = f (\theta)

x = a(\theta - \sin{\theta})

\displaystyle \frac{dx}{d\theta} = \frac{d}{d\theta} [a(\theta - \sin{\theta})]

\displaystyle \frac{dx}{d\theta} = a \frac{d}{d\theta} (\theta - \sin{\theta})

\displaystyle \frac{dx}{d\theta} = a(1 - \cos{\theta})

\displaystyle \frac{d}{d\theta} [f(\theta)] = a(1 - \cos{\theta})

\displaystyle f' (\theta) = a(1 - \cos{\theta})

Así que

y = \phi (\theta) = a(1 - \cos{\theta})
\displaystyle f' (\theta) = a(1 - \cos{\theta})

Tomando la fórmula

\displaystyle \text{Area} = \int_{\theta_1}^{\theta_2}{\phi (\theta) \, f' (\theta) \, d\theta}

Y sustituyendo

\displaystyle \text{Area} = \int_0^{2\pi}{a(1 - \cos{\theta}) \cdot a(1 - \cos{\theta}) \, d\theta}

\displaystyle \text{Area} = \int_0^{2\pi}{a^2 (1 - \cos{\theta})^2 \, d\theta} = a^2 \int_0^{2\pi}{(1 - \cos{\theta})^2 \, d\theta}

\displaystyle \text{Area} = a^2 \int_0^{2\pi}{(1 - 2 \cos{\theta} + \cos^2{\theta}) \, d\theta} = a^2 \int_0^{2\pi}{d\theta} - 2a^2 \int_0^{2\pi}{\cos{\theta} \, d\theta} + a^2

\displaystyle \text{Area} = a^2 \int_0^{2\pi}{d\theta} - 2a^2 \int_0^{2\pi}{\cos{\theta} \, d\theta} + a^2 \int_0^{2\pi}{\cos^2{\theta} \, d\theta}

En la tercera integral, aplicando la fórmula \displaystyle \cos^2{\theta} = \frac{1}{2} + \frac{1}{2} \cos{2\theta}, resulta

\displaystyle \text{Area} = a^2 \int_0^{2\pi}{d\theta} - 2a^2 \int_0^{2\pi}{\cos{\theta} \, d\theta} + a^2 \int_0^{2\pi}{\left(\frac{1}{2} + \frac{1}{2} \cos{2\theta} \right) \, d\theta}

\displaystyle \text{Area} = a^2 \int_0^{2\pi}{d\theta} - 2a^2 \int_0^{2\pi}{\cos{\theta} \, d\theta} + \frac{1}{2} a^2 \int_0^{2\pi}{d\theta} + \frac{1}{2} a^2 \int_0^{2\pi}{\cos{2\theta} \, d\theta}

\displaystyle \text{Area} = \frac{3}{2} a^2 \int_0^{2\pi}{d\theta} - 2a^2 \int_0^{2\pi}{\cos{\theta} \, d\theta} + \frac{1}{2} a^2 \int_0^{2\pi}{\cos{2\theta} \, d\theta}

\displaystyle \text{Area} = \frac{3}{2} a^2 \underbrace{\int_0^{2\pi}{d\theta}}_{1} - 2a^2 \underbrace{\int_0^{2\pi}{\cos{\theta} \, d\theta}}_{2} + \frac{1}{2} a^2 \underbrace{\int_0^{2\pi}{\cos{2\theta} \, d\theta}}_{3}

La primera integral es similar a

\displaystyle \int{dv} = v + C

Entonces

\displaystyle \int{d\theta} = \theta + C

La segunda integral es similar a

\displaystyle \int{\cos{v} \, dv} = \sin{v} + C

Entonces

\displaystyle \int{\cos{\theta} \, d\theta} = \sin{\theta} + C

La tercera integral es similar a

\displaystyle \int{\cos{v} \, dv} = \sin{v} + C

Analizando la variable v

v=2\theta
\displaystyle dv = 2 \, d\theta \rightarrow d\theta = \frac{1}{2} \, dv

Su resultado es

\displaystyle \int{\cos{2\theta} \, d\theta} = \int{\cos{v} \cdot \frac{1}{2} \, dv}

\displaystyle \int{\cos{2\theta} \, d\theta} = \frac{1}{2} \int{\cos{v} \, dv} = \frac{1}{2} \sin{v} + C

\displaystyle \int{\cos{2\theta} \, d\theta} = \frac{1}{2} \sin{2\theta} + C

Regresando, sustituyendo y cambiando la variable por los límites indicados en cada integral, resulta

\displaystyle \text{Area} = \frac{3}{2} a^2 \int_0^{2\pi}{d\theta} - 2a^2 \int_0^{2\pi}{\cos{\theta} \, d\theta} + \frac{1}{2} a^2 \int_0^{2\pi}{\cos{2\theta} \, d\theta}

\displaystyle \text{Area} = \frac{3}{2} a^2 [\theta + C]_0^{2\pi} - 2a^2 [\sin{\theta} + C]_0^{2\pi} + \frac{1}{2} a^2 \left[\frac{1}{2} \sin{2\theta} + C\right]_0^{2\pi}

\displaystyle \text{Area} = \frac{3}{2} a^2 (2\pi - 0) - 2a^2 (\sin{2\pi} - \sin{0}) + \frac{1}{2} a^2 \left(\frac{1}{2} \sin{4\pi} - \frac{1}{2} \sin{0} \right)

\displaystyle \text{Area} = \frac{3}{2} a^2 (2\pi) - 2a^2 (0) + \frac{1}{2} a^2 (0) = 3a^2 \pi

Finalmente, área de la arcada de la cicloide es

\displaystyle \therefore \text{Area} = 3a^2 \pi \ \text{u}^2

Problema 2. Hallar el área de la cardioide x=a(2 \cos{\theta} - \cos{\theta}), y = a(2 \sin{\theta} - \sin{2\theta}).

Solución. Se realiza una tabulación mediante las ecuaciones de la cicloide desde 0 hasta 2π (donde se ha considerado el valor de a=1 para llevar a cabo sólo la tabulación).

valores5

Graficando la función

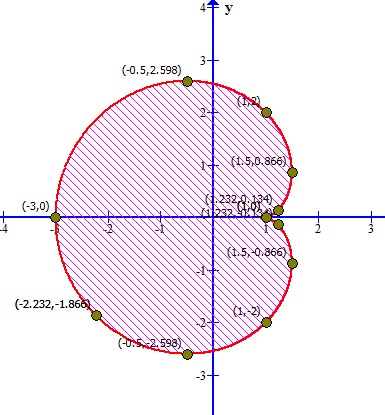
figura 4.2.7
Figura 7. Representación gráfica de la cardioide.

Entonces, la arcada se forma desde \theta = 0 hasta \theta = 2\pi. Después determinando la primera derivada de la ecuación x, se tiene lo siguiente

\displaystyle x = f(\theta)

\displaystyle x = a(2 \cos{\theta} - \cos{2\theta})

\displaystyle \frac{dx}{d\theta} = \frac{d}{d\theta} [a(2 \cos{\theta} - \cos{2\theta})]

\displaystyle \frac{dx}{d\theta} = a \frac{d}{d\theta} (2 \cos{\theta} - \cos{2\theta})

\displaystyle \frac{dx}{d\theta} = a(-2 \sin{\theta} + 2 \sin{2\theta})

\displaystyle f' (\theta) = 2a(-\sin{\theta} + \sin{2\theta})

Así que

y = \phi (\theta) = a(2 \sin{\theta} - \sin{2\theta})
\displaystyle f' (\theta) =2a(-\sin{\theta} + \sin{2\theta})

Tomando la fórmula

\displaystyle \text{Area} = \int_{\theta_1}^{\theta_2}{\phi(\theta) f' (\theta) \, d\theta}

Y sustituyendo

\displaystyle \text{Area} = \int_0^{2\pi}{a (2 \sin{\theta} - \sin{2\theta}) \cdot 2a(-\sin{\theta} + \sin{2\theta}) \, d\theta}

Pero el área que describe la cardioide es el doble del área comprendida desde 0 hasta \pi. Por tanto, se antepondrá “-2” a la forma del área.

\displaystyle \text{Area} = \int_0^{2\pi}{a (2 \sin{\theta} - \sin{2\theta}) \cdot 2a(-\sin{\theta} + \sin{2\theta}) \, d\theta}

\displaystyle \text{Area} = -2\int_0^{\pi}{a (2 \sin{\theta} - \sin{2\theta}) \cdot 2a(-\sin{\theta} + \sin{2\theta}) \, d\theta}

\displaystyle \text{Area} = -4a^2 \int_0^{\pi}{(2 \sin{\theta} - \sin{2\theta}) \cdot (-\sin{\theta} + \sin{2\theta}) \, d\theta}

\displaystyle \text{Area} = -4a^2 \int_0^{\pi}{(-2 \sin^2{\theta} + 2 \sin{\theta} \sin{2\theta} + \sin{\theta} \sin{2\theta} - \sin^2{2\theta}) \, d\theta}

\displaystyle \text{Area} = -4a^2 \int_0^{\pi}{(-2 \sin^2{\theta} + 3 \sin{\theta} \sin{2\theta} - \sin^2{2\theta}) \, d\theta}

\displaystyle \text{Area} = 8a^2 \int_0^{\pi}{\sin^2{\theta} \, d\theta} - 12a^2 \int_0^{\pi}{\sin{\theta} \sin{2\theta} \, d\theta} + 4a^2 \int_0^{\pi}{\sin^2{2\theta} \, d\theta}

En la primera integral, aplicando la fórmula \displaystyle \sin^2{\theta} = \frac{1}{2} - \frac{1}{2} \cos{2\theta}, y en la tercera integral, aplicando la fórmula \displaystyle \sin^2{2\theta} = \frac{1}{2} - \frac{1}{2} \cos{4\theta}, se tiene que

\displaystyle \text{Area} = 8a^2 \int_0^{\pi}{(\frac{1}{2} - \frac{1}{2} \cos{2\theta}) \, d\theta} - 12a^2 \int_0^{\pi}{\sin{\theta} \sin{2\theta} \, d\theta} + 4a^2 \int_0^{\pi}{(\frac{1}{2} - \frac{1}{2} \cos{4\theta}) \, d\theta}

\displaystyle \text{Area} = \frac{8}{2} a^2 \int_0^{\pi}{d\theta} - \frac{8}{2} a^2 \int_0^{\pi}{\cos{2\theta} \, d\theta} - 12a^2 \int_0^{\pi}{\sin{\theta} \sin{2\theta} \, d\theta} + \frac{4}{2} a^2 \int_0^{\pi}{d\theta} - \frac{4}{2} a^2 \int_0^{\pi}{\cos{4\theta} \, d\theta}

\displaystyle \text{Area} = 4a^2 \int_0^{\pi}{d\theta} - 4a^2 \int_0^{\pi}{\cos{2\theta} \, d\theta} - 12a^2 \int_0^{\pi}{\sin{\theta} \sin{2\theta} \, d\theta} + 2a^2 \int_0^{\pi}{d\theta} - 2a^2 \int_0^{\pi}{\cos{4\theta} \, d\theta}

\displaystyle \text{Area} = 6a^2 \int_0^{\pi}{d\theta} - 4a^2 \int_0^{\pi}{\cos{2\theta} \, d\theta} - 12a^2 \int_0^{\pi}{\sin{\theta} \sin{2\theta} \, d\theta} - 2a^2 \int_0^{\pi}{\cos{4\theta} \, d\theta}

\displaystyle \text{Area} = 6a^2 \underbrace{\int_0^{\pi}{d\theta}}_{1} - 4a^2 \underbrace{\int_0^{\pi}{\cos{2\theta} \, d\theta}}_{2} - 12a^2 \underbrace{\int_0^{\pi}{\sin{\theta} \sin{2\theta} \, d\theta}}_{2} - 2a^2 \underbrace{\int_0^{\pi}{\cos{4\theta} \, d\theta}}_{3}

La primera integral es similar a

\displaystyle \int{dv} = v + C

Entonces

\displaystyle \int{d\theta} = \theta + C

La segunda integral es similar a

\displaystyle \int{\cos{v} \, dv} = \sin{v} + C

Analizando la variable v

v = 2\theta
\displaystyle dv = 2 \, d\theta \rightarrow d\theta = \frac{1}{2} \, dv

 Su resultado es

\displaystyle \int{\cos{2\theta} \, d\theta} = \int{\cos{v} \cdot \frac{1}{2} \, dv}

\displaystyle \int{\cos{2\theta} \, d\theta} = \frac{1}{2} \int{\cos{v} \, dv} = \frac{1}{2} \sin{v} + C

\displaystyle \int{\cos{2\theta} \, d\theta} = \frac{1}{2} \sin{2\theta} + C

La tercera integral debe acomodarse de la siguiente manera

\displaystyle \int{\sin{\theta} \sin{2\theta} \, d\theta} = \int{\sin{2\theta} \sin{\theta} \, d\theta}

Ahora tiene la forma \displaystyle \int{\sin{mu} \sin{nu} \, du}, donde m=2 y n=1. Entonces, aplicando la fórmula de integración directa para este caso

\displaystyle \int{\sin{mu} \sin{nu} \, du} = -\frac{1}{2(m+n)} \sin{(m+n)u} + \frac{1}{2(m-n)} \sin{(m-n)u} + C

Sustituyendo los valores de m y n, se tiene

\displaystyle \int{\sin{2\theta} \sin{\theta} \, d\theta} = -\frac{1}{2(2+1)} \sin{(2+1)\theta} + \frac{1}{2(2-1)} \sin{(2-1)\theta} + C

\displaystyle \int{\sin{2\theta} \sin{\theta} \, d\theta} = -\frac{1}{2(3)} \sin{3\theta} + \frac{1}{2(1)} \sin{\theta} + C = -\frac{1}{6} \sin{3\theta} + \frac{1}{2} \sin{\theta} + C

La cuarta integral es similar a

\displaystyle \int{\cos{v} \, dv} = \sin{v} + C

Analizando la variable v

v = 4\theta
\displaystyle dv = 4 \, d\theta \rightarrow d\theta = \frac{1}{4} \, dv

El resultado de esta integral es

\displaystyle \int{\cos{4\theta} \, d\theta} = \int{\cos{v} \cdot \frac{1}{4} \, dv}

\displaystyle \int{\cos{4\theta} \, d\theta} = \frac{1}{4} \int{\cos{v} \, dv} = \frac{1}{4} \sin{v} + C

\displaystyle \int{\cos{4\theta} \, d\theta} = \frac{1}{4} \sin{4\theta} + C

Regresando y sustituyendo los valores obtenidos

\displaystyle \text{Area} = 6a^2 \int_0^{\pi}{d\theta} - 4a^2 \int_0^{\pi}{\cos{2\theta} \, d\theta} - 12a^2 \int_0^{\pi}{\sin{\theta} \sin{2\theta} \, d\theta} - 2a^2 \int_0^{\pi}{\cos{4\theta} \, d\theta}

\displaystyle \text{Area} = 6a^2 [\theta + C]_0^\pi - 4a^2 \left[\frac{1}{2} \sin{2\theta} + C \right]_0^{\pi} - 12a^2 \left[- \frac{1}{6} \sin{3\theta} + \frac{1}{2} \sin{\theta} + C\right]_0^{\pi} - 2a^2 \left[\frac{1}{4} \sin{4\theta} + C\right]_0^{\pi}

\displaystyle \text{Area} = 6a^2 (\pi - 0) - 4a^2 (\frac{1}{2} \sin{2\pi} - \frac{1}{2} \sin{0}) - 12a^2 (-\frac{1}{6} \sin{3\pi} + \frac{1}{2} \sin{\pi} + \frac{1}{6} \sin{0} - \frac{1}{2} \sin{0}) - 2a^2 (\frac{1}{4} \sin{4\pi} - \frac{1}{4} \sin{0})

\displaystyle \text{Area} = 6a^2 (\pi) - 4a^2 (0) - 12a^2 \left[ -\frac{1}{6} (0) + \frac{1}{2} (0)\right] - 2a^2 \frac{1}{2} (0) = 6a^2 \pi

Finalmente, el área de la cardioide es

\displaystyle \therefore \text{Area} = 6a^2 \pi \ \text{u}^2

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.