La integral definida y el origen del área bajo una curva. Cálculo integral.

Diferencial del área bajo una curva

Sea la función $\phi (x)$ y sea $y = \phi (x)$ la ecuación de la curva $AB$ .

Con base en la figura 1, sea $CD$ la ordenada fija, $EF$ la ordenada de variable y $A$ la medida del área $CEFD$ . Cuando $x$ toma un incremento pequeño $\Delta x$ , $A$ toma un incremento $\Delta A = EGJF$ .

Completando los rectángulos $EGHF$ y $EGJI$ , se observa que

$\text{area EGHF} < \text{area EGJF} < \text{area EGJI}$

es decir,

$EF(\Delta x) < \Delta A < GJ(\Delta x)$

y dividiendo entre $\Delta x$ , resulta:

$\displaystyle EF < \frac{\Delta A}{\Delta x} < GJ$

Si $\Delta x = 0$ , entonces, puesto que $EF$ queda fija y $GJ$ tiende hacia $EF$ como límite (dado que y es una función continua de $x$ ), se tiene que

$\displaystyle \frac{dA}{dx} = y(=EF)$

Empleando diferenciales, resulta

$dA = y \, dx$

Teorema sobre la diferencial del área bajo una curva

La diferencial del área limitada por una curva cualquiera, el eje de las $x$ , una ordenada fija y una ordenada variable es igual al producto de la ordenada variable por la diferencial de la abscisa correspondiente.

La integral definida

Del teorema anterior se sigue que si la curva $AB$ es el lugar geométrico de $y = \phi (x)$ , entonces $dA = y \quad dx$ , es decir, $dA = \phi (x) \, dx$ , siendo $dA$ la diferencial del área entre la curva, el eje de las $x$ y dos ordenadas.

Integrando, se tiene que

$dA = \phi (x) \, dx$

$\displaystyle \int{dA} = \int{\phi (x) \, dx}$

$A = f(x) + C$

Para determinar el valor de la constante de integración $C$ , se hace notar que $A=0$ cuando $x=a$ . Sustituyendo estos valores en la integral obtenida, resulta:

$0=f(a)+C$

$C=-f(a)$

Por tanto, se tiene

$A = f(x) - f(a)$

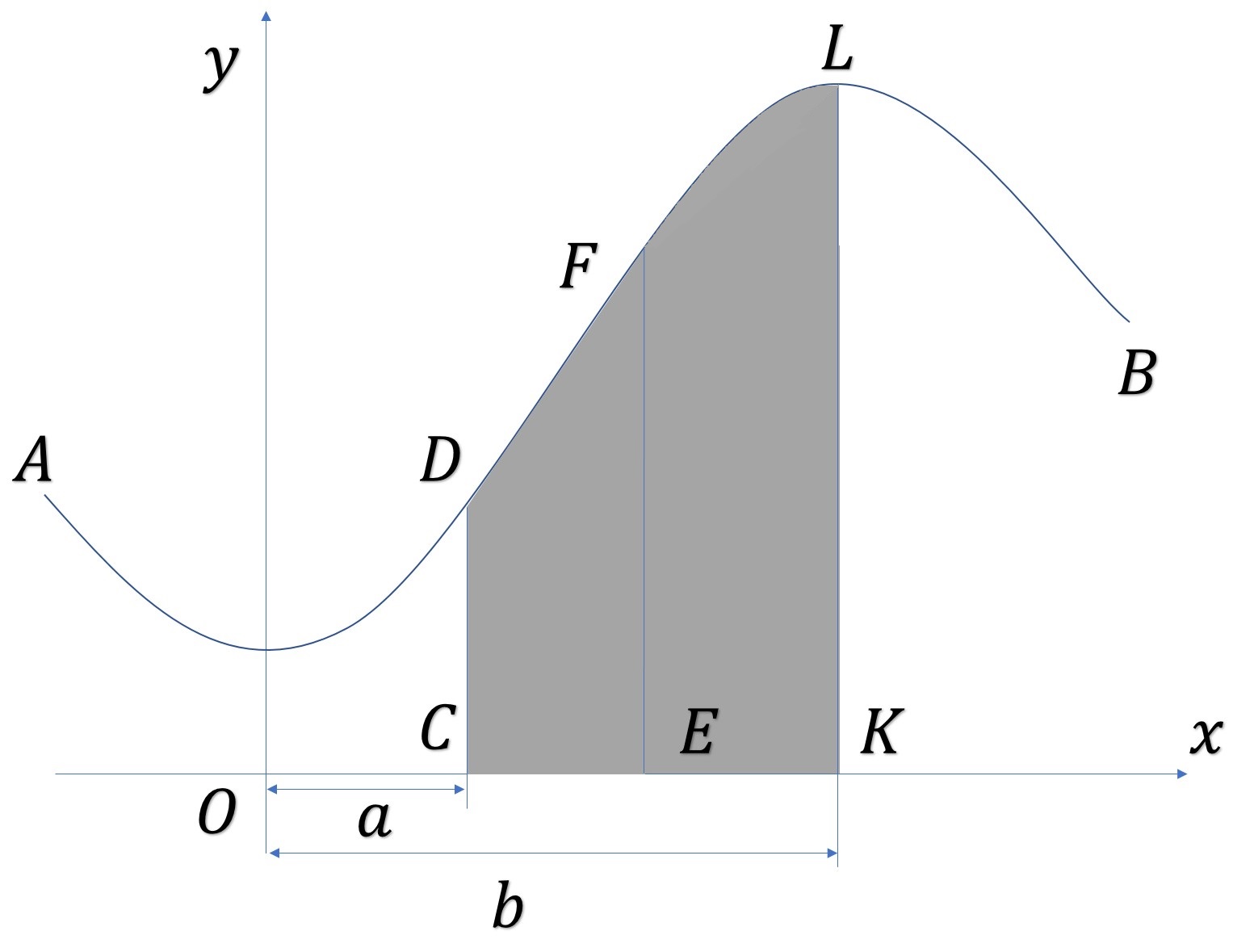
Con base a la figura 2, se tiene que el área $CKLD$ , cuando $x=b$ es

$\displaystyle \text{area } CKLD = f(b) - f(a)$

Teorema sobre la integral definida

La diferencia de los valores de $\displaystyle \int{y \, dx}$ para $x=a$ y $x=b$ da el área limitada por la curva cuya ordenada es $y$ , el eje de las $x$ y las ordenadas que corresponden a $x=a$ y $x=b$ . Simbólicamente se expresa:

$\displaystyle \int_a^b{y \, dx}$

Y se lee: la integral desde $a$ hasta $b$ de $y \, dx$ .

La operación anterior se denomina integración entre límites; donde $a$ es el límite inferior y $b$ es el límite superior.

Por tanto, la expresión $\displaystyle \int_a^b{y \, dx}$ se llama integral definida.

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web. Ver todas las entradas de Cesar Reyes

Deja un comentario Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.