Fórmula de los trapecios. Cálculo integral.

Introducción

La aplicación de la fórmula de los trapecios es útil cuando la integración en $\displaystyle \int_a^b{f(x) \, dx}$ es difícil o no se efectúa en términos de funciones elementales. El valor numérico exacto de $\displaystyle \int_a^b{f(x) \, dx}$ es la medida del área de la superficie limitada por la curva $y=f(x)$ , el eje de las $x$ y las ordenadas $x=a$ y $x=b$ .

El valor de esta área puede determinarse, aproximadamente, sumando trapecios, tal como se observa en la figura 1.

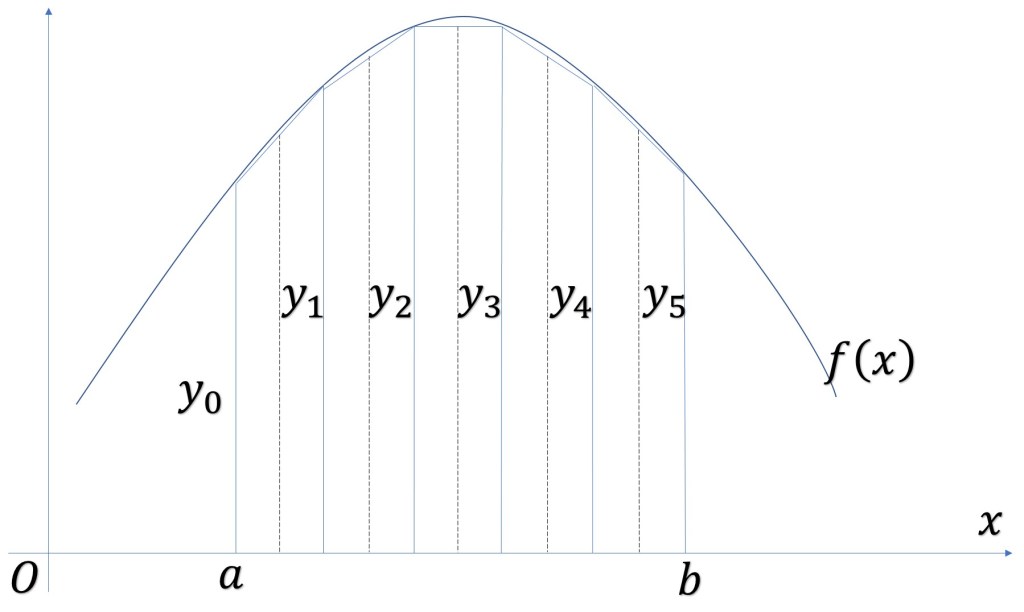
figura 4.3.1 — Figura 1. Representación gráfica de una función f(x) dividida en «n» rectángulos.

Dividiendo el segmento $b-a$ del semieje $OX$ en $n$ partes iguales, y sea $\Delta x$ la longitud de cada parte, es decir

$\displaystyle \Delta x = \frac{b-a}{n}$

Sean las abscisas de los puntos de división de la función

$x_0 = a$ , $x_1$ , $x_2$ , $x_3$ , …, $x_n = b$

Trazar en estos puntos las coordenadas correspondientes de la curva $y=f(x)$ , y sean éstas:

$y_0 = f(x_0 )$ , $y_1=f(x_1 )$ , $y_2=f(x_2 )$ , $y_3=f(x_3 )$ ,⋯, $y_n=f(x_n )$

Se unen las extremidades de las ordenadas consecutivas por líneas rectas (cuerdas); de esta manera se formarán trapecios. Puesto que el área de un trapecio es igual a la semisuma de las bases por la altura, se tiene

$\displaystyle \frac{1}{2} (y_0+y_1 )\Delta x =$ área del primer trapecio,

$\displaystyle \frac{1}{2} (y_1+y_2 ) \Delta x =$ área del segundo trapecio,

$\displaystyle \frac{1}{2} (y_2+y_3 ) \Delta x =$ área del tercer trapecio,

…

$\displaystyle \frac{1}{2} (y_{n-1} + y_n ) \Delta x =$ área del enésimo trapecio

Sumando, se tiene la fórmula del área de todos los trapecios, y es

$\displaystyle \text{Area total} = \left( \frac{1}{2} y_0 + y_1 + y_2 + y_3 + \cdots + y_{n-1} + \frac{1}{2} y_n \right) \Delta x$

Es necesario toman en cuenta que cuanto mayor sea el número de intervalos (cuanto más pequeño sea $\Delta x$ ) tanto más se aproximará el área total de los trapecios al área bajo la curva.

Problemas resueltos

Problema 1. Empleando la fórmula de los trapecios, calcular el área aproximada de la curva $y=x^2$ dividiendo de $x=2$ a $x=8$ en seis intervalos. Comparar el resultado obtenido, efectuando la integración directa.

Solución. Primero, se calcula la longitud de cada intervalo

$\displaystyle \Delta x = \frac{b-a}{n}$

$\displaystyle \Delta x = \frac{8-2}{6} = \frac{6}{6} = 1$

$\displaystyle \Delta x = 1$

Después, se tabula la función con los valores de la abscisa sucesivos de tamaño $\Delta x = 1$ , desde $x=2$ hasta $x=8$ .

Los valores obtenidos en la tabla se sustituyen en la fórmula de los trapecios.

$\displaystyle \text{Area total} = \left(\frac{1}{2} y_0 + y_1 + y_2 + y_3 + \cdots + y_{n-1} + \frac{1}{2} y_n \right) \Delta x$

$\displaystyle \text{Area total} = \left( \frac{1}{2} y_0 + y_1 + y_2 + y_3 + y_4 + y_5 + \frac{1}{2} y_6 \right) \Delta x$

$\displaystyle \text{Area total} = \left[\frac{1}{2} (4) + 9 + 16 + 25 + 36 + 49 + \frac{1}{2} (64) \right] (1) = (2+135+32)(1)$

$\displaystyle \text{Area total} =(169)(1)=169$

Finalmente

$\displaystyle \therefore \text{Area total} = 169 \ \text{u}^2$

Aplicando la integración directa

$\displaystyle \text{Area} = \int_a^b{y \, dx} = \int_2^8{x^2 \, dx}$

Resolviéndolo como una integral indefinida

$\displaystyle \int_2^8{x^2 \, dx} \quad \rightarrow \quad \int{x^2 \, dx}$

Es similar a

$\displaystyle \int{v^n \, dv} = \frac{1}{n+1} v^{n+1} + C$

Entonces

$\displaystyle \int{x^2 \, dx} = \frac{1}{2+1} x^{2+1} + C = \frac{1}{3} x^3 + C$

Reemplazando la variable $x$ por los valores de los límites, resulta

$\displaystyle \int_2^8{x^2 \, dx} = \left[\frac{1}{3} x^3 + C \right]_2^8$

$\displaystyle \int_2^8{x^2 \, dx} = \frac{1}{3} (8)^3 - \frac{1}{3} (2)^3 = \frac{512}{3} - \frac{8}{3}$

$\displaystyle \int_2^8{x^2 \, dx} = \frac{504}{3} = 168$

Por tanto

$\displaystyle \text{Area} = \int_2^8{x^2 \, dx}$

$\displaystyle \therefore \text{Area} = 168 \ \text{u}^2$

Problema 2. Efectuando la fórmula de los trapecios, calcular el área aproximada para la curva $x^2+y^2=64$ , dividiendo de $x=4$ a $x=8$ en ocho intervalos. Comparar el resultado obtenido efectuando la integración directa.

Solución. Primero, se calcula la longitud de cada intervalo

$\displaystyle \Delta x = \frac{b-a}{n}$

$\displaystyle \Delta x = \frac{8-4}{8} = \frac{4}{8} = 0.5$

$\Delta x = 0.5$

Después, de la función brindada, se despeja la variable $y$ .

$x^2+y^2=64$

$y^2=64-x^2$

$\displaystyle y = \pm \sqrt{64-x^2}$

Se toma solo la parte positiva de la raíz, entonces

$\displaystyle y = \sqrt{64-x^2}$

Luego, se tabula la función con los valores de la abscisa sucesivos de tamaño $\Delta x = 0.5$ , desde $x=4$ hasta $x=8$ .

Los valores obtenidos y mostrados en la tabla se van a sustituir en la fórmula de los trapecios.

$\displaystyle \text{Area total} = \left(\frac{1}{2} y_0+y_1+y_2+y_3+ \cdots +y_{n-1}+\frac{1}{2} y_n \right) \Delta x$

$\displaystyle \text{Area total} = \left(\frac{1}{2} y_0+y_1+y_2+y_3+y_4+y_5+y_6+y_7+\frac{1}{2} y_8 \right) \Delta x$

$\displaystyle \text{Area total} = \left[\frac{1}{2} (6.928)+6.614+6.244+5.809+5.291+4.663+3.872+2.783+\frac{1}{2} (0) \right] (0.5)$

$\displaystyle \text{Area total} = (3.464+35.276+0)(0.5)$

$\text{Area total} = (38.74)(0.5) = 19.37$

Finalmente

$\therefore \text{Area total} = 19.37 \ \text{u}^2$

Por integración directa, se toma la fórmula para calcular el área.

$\displaystyle \text{Area} = \int_a^b{y \, dx} = \int_4^8{\sqrt{64-x^2} \, dx}$

Resolviéndolo como una integral indefinida

$\displaystyle \int_4^8{\sqrt{64-x^2} \, dx} \quad \rightarrow \quad \int{\sqrt{64-x^2} \, dx}$

Es similar a

$\displaystyle \int{\sqrt{a^2-v^2} \, dv} = \frac{1}{2} v \sqrt{a^2-v^2} + \frac{1}{2} a^2 \arcsin{(\frac{v}{a})} + C$

Analizando las variables

El resultado de esta integral es

$\displaystyle \int{\sqrt{64-x^2} \, dx} = \frac{1}{2} x\sqrt{64-x^2} + \frac{1}{2} (64) \arcsin{(\frac{x}{8})} + C$

$\displaystyle \int{\sqrt{64-x^2} \, dx} = \frac{1}{2} x\sqrt{64-x^2} + 32 \arcsin{(\frac{x}{8})} + C$

Regresando y reemplazando la variable x por los límites indicados, resulta

$\displaystyle \int_4^8{\sqrt{64-x^2} \, dx} = \left[ \frac{1}{2} x\sqrt{64-x^2} + 32 \arcsin{(\frac{x}{8})} + C\right]_4^8$

$\displaystyle \int_4^8{\sqrt{64-x^2} \, dx} = \left[\frac{1}{2} (8) \sqrt{64-64} ) +32 \arcsin{(\frac{8}{8})} \right] -\left[ \frac{1}{2} (4) \sqrt{64-16} + 32\arcsin{(\frac{4}{8})} \right]$

$\displaystyle \int_4^8{\sqrt{64-x^2} \, dx} = (0+32 \arcsin{1}) - \left[2\sqrt{52} + 32 \arcsin{(\frac{1}{2})} \right]$

$\displaystyle \int_4^8{\sqrt{64-x^2} \, dx} = 32(\frac{1}{2} \pi) - 2\sqrt{52} - 32 \arcsin{\frac{1}{2}} = 19.088$

Finalmente

$\displaystyle\therefore \text{Area} = 19.088 \ \text{u}^2$

Problema 3. Empleando la fórmula de los trapecios, calcular el área aproximada para la curva $xy=1$ , dividiendo de $x=3$ a $x=10$ en siete intervalos. Compara el resultado obtenido efectuando la integración directa.