Introducción

En la fórmula \displaystyle \int_a^b{y \, dx}, a es menor que b (a<b). Puesto que ahora interpretamos el primer miembro como el límite de la suma de n términos que resultan de y_i \Delta x_i con i = 1, 2, 3, \cdots, n, se sigue que cuando y es negativo cada término de esa suma será negativo, y \displaystyle \int_a^b{y \, dx} resultará con signo negativo. Lo anterior significa que el área está debajo del eje de las x.

Problemas resueltos

Problema 1. Calcular el área de una arcada de la sinusoide y = \sin{x}.

Solución. Realizando una tabulación con la ecuación de la sinusoide y comenzando desde x=0 hasta x=2\pi.

tabla4.4.2
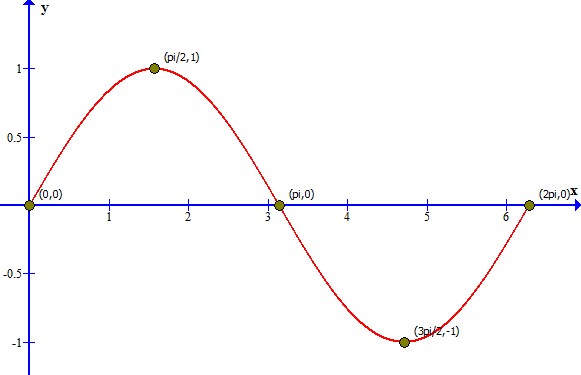
figura 4.4.5
Figura 1. Representación gráfica de la función y=sen(x).

Si se toma el área de una arcada desde x=0 hasta x=\pi, tomando la fórmula para determinar el área en el eje x es

\displaystyle \text{Area} = \int_a^b{y \, dx} = \int_0^{\pi}{\sin{x} \, dx}

Resolviéndolo como una integral indefinida

\displaystyle \int{\sin{x} \, dx} = -\cos{x} + C

Y reemplazando la variable x por los límites correspondientes, resulta

\displaystyle \int_0^{\pi}{\sin{x} \, dx} = [-\cos{x} + C]_0^{\pi}

\displaystyle \int_0^{\pi}{\sin{x} \, dx} = [-\cos{\pi} + C] - [-\cos{0} + C] = -(-1) + (1)

\displaystyle \int_0^{\pi}{\sin{x} \, dx} = 2

Así que

\displaystyle \text{Area} = \int_0^{\pi}{\sin{x} \, dx}

\displaystyle \therefore \text{A} = 2 \ \text{u}^2

Si se toma el área de una arcada desde x=\pi hasta x=2\pi, tomando la fórmula para determinar el área en el eje x es

\displaystyle \text{Area} = \int_a^b{y \, dx} = \int_{\pi}^{2\pi}{\sin{x} \, dx}

Resolviéndolo como una integral indefinida

\displaystyle \int{\sin{x} \, dx} = -\cos{x} + C

Y reemplazando la variable x por los límites correspondientes, resulta

\displaystyle \int_{\pi}^{2\pi}{\sin{x} \, dx} = [-\cos{x} + C]_{\pi}^{2\pi}

\displaystyle \int_{\pi}^{2\pi}{\sin{x} \, dx} = [-\cos{2\pi} + C] - [-\cos{\pi} + C] = -(1)+(-1)

\displaystyle \int_{\pi}^{2\pi}{\sin{x} \, dx} = - 2

Entonces,

\displaystyle \text{Area} = \int_{\pi}^{2\pi}{\sin{x} \, dx}

\displaystyle \text{Area} = -2 \ \text{u}^2

Comparando ambos resultados

Área de la primera arcada (desde 0 hasta )  \displaystyle \int_0^{\pi}{\sin{x} \, dx} = 2Área ubicada por arriba del eje
Área de la segunda arcada (desde  hasta 2 )  \displaystyle \int_{\pi}^{2\pi}{\sin{x} \, dx} = -2Área ubicada por debajo del eje

Finalmente, el área de una arcada (sin importar los límites tomados) es

\displaystyle \text{Area} = 2 \ \text{u}^2

Problema 2. Calcular el área limitada por la curva x = 3 + \cos{\theta} y y=4 \sin{\theta}.

Solución. Primero se realiza una tabulación con las ecuaciones brindadas desde 0 hasta 2π con incremento de π/6.

tabla4.4.3

Graficando la función, se tiene lo siguiente

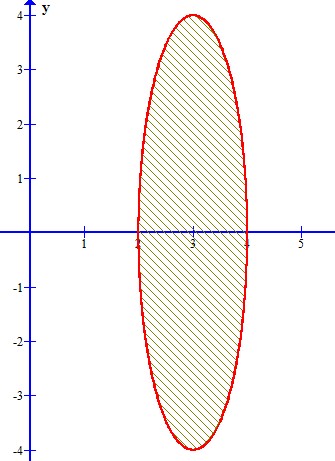
figura 4.4.6
Figura 2. Representación gráfica de las ecuaciones paramétricas dadas por el problema resuelto no. 4.

Las ecuaciones de la curva están en forma paramétrica, entonces, se toma la siguiente fórmula

\displaystyle \text{Area} = \int_{\theta_1}^{\theta_2}{\phi (\theta) f' (\theta) \, d\theta}

Donde

\displaystyle \phi (\theta) = y

\displaystyle \phi (\theta) = 4 \sin{\theta}

Y

\displaystyle f(\theta) = x

\displaystyle f(\theta) = 4 + \cos{\theta}

Determinando la primera derivada de f(\theta)

\displaystyle f' (\theta) = -\sin{\theta}

Y su diferencial es

\displaystyle \frac{d}{d\theta} f(\theta) = -\sin{\theta}

La gráfica comienza desde θ=0 y termina hasta θ=2π y se observa que θ varía de derecha a izquierda, por tanto, el área que describe la curva dada será el doble del área comprendida e irá desde 0 hasta π. Entonces

\displaystyle \text{Area} = \int_{\theta_1}^{\theta_2}{\phi (\theta) f' (\theta) \, d\theta}

\displaystyle \text{Area} = -2\int_0^{\pi}{4 \sin{\theta} (-\sin{\theta}) \, d\theta}

\displaystyle \text{Area} = 8\int_0^{\pi}{\sin^2{\theta} \, d\theta}

Resolviéndolo como una integral

\displaystyle \int{\sin^2{\theta} \, d\theta}

Por el método de integración trigonométrica para funciones seno de producto de potencias pares, se toma la siguiente fórmula \displaystyle \sin^2{\theta} = \frac{1}{2} - \frac{1}{2} \cos{2\theta}

\displaystyle \int{\sin^2{\theta} \, d\theta} = \int{(\frac{1}{2} - \frac{1}{2} \cos{2\theta}) \, d\theta}

\displaystyle \int{\sin^2{\theta} \, d\theta} = \frac{1}{2} \int{d\theta} - \frac{1}{2} \int{\cos{2\theta} \, d\theta}

La primera integral tiene el siguiente resultado

\displaystyle \int{d\theta} = \theta + C

Y la segunda integral tiene el siguiente resultado

\displaystyle \int{\cos{2\theta} \, d\theta} = \frac{1}{2} \sin{2\theta} + C

Regresando

\displaystyle \int{\sin^2{\theta} \, d\theta} = \frac{1}{2} \int{d\theta} - \frac{1}{2} \int{\cos{2\theta} \, d\theta}

\displaystyle \int{\sin^2{\theta} \, d\theta} = \frac{1}{2} (\theta + C) - \frac{1}{2} (\frac{1}{2} \sin{2\theta} + C)

\displaystyle \int{\sin^2{\theta} \, d\theta} = \frac{1}{2} \theta - \frac{1}{4} \sin{2\theta} + C

Reemplazando la variable θ por los límites correspondientes, resulta

\displaystyle \int_0^{\pi}{\sin^2{\theta} \, d\theta} = \left[\frac{1}{2} \theta - \frac{1}{4} \sin{2\theta} + C\right]_0^{\pi}

\displaystyle \int_0^{\pi}{\sin^2{\theta} \, d\theta} = \left[\frac{1}{2} (\pi) - \frac{1}{4} \sin{2\pi} \right] - \left[\frac{1}{2} (0) - \frac{1}{4} \sin{2(0)} \right]

\displaystyle \int_0^{\pi}{\sin^2{\theta} \, d\theta} = \left[ \frac{1}{2}(\pi)- 0 \right] - \left[\frac{1}{2} (0) - \frac{1}{4} (0) \right] = \frac{\pi}{2}

Finalmente, el área de la curva es

\displaystyle \text{Area} = 8 \int_0^{\pi}{\sin^2{\theta} \, d\theta}

\displaystyle \text{Area} = 8 \left(\frac{\pi}{2} \right)

\displaystyle \therefore \text{Area} = 4 \pi

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.