Área limitada por dos curvas al intersecarse en más de dos puntos. Cálculo integral.

Introducción

Cuando dos curvas se cortan en más de dos puntos, entonces, para determinar el área de la región comprendida entre ellas, se debe buscar todos los puntos de intersección y comprobar cada intervalo precisado por las curvas cuál de ellas está por encima de la otra.

Problemas resueltos

Problema 1. Calcular el área de la región acotada por las curvas $f(x)=x^3-2x^2+x-1$ y $g(x)=3x-x^2-1$ .

Solución. Primero se determinan los puntos de intersección de ambas curvas dadas, partiendo de la condición f(x)≥g(x). Entonces

$f(x) = g(x)$

$x^3-2x^2+x-1=3x-x^2-1$

$x^3-2x^2+x-1-3x+x^2+1=0$

$x^3-x^2-2x=0$

$x(x^2-x-2)=0$

$x(x-2)(x+1)=0$

Los valores de $x$ son $x=-1$ , $x=0$ y $x=2$ . Ahora, se realiza la tabulación con las funciones $f(x)$ y $g(x)$ desde $x=-1$ hasta $x=2$ con un incremento de 0.5.

Graficando las funciones $f(x)$ y $g(x)$ y localizando los valores de $x$ obtenidos, resulta lo siguiente

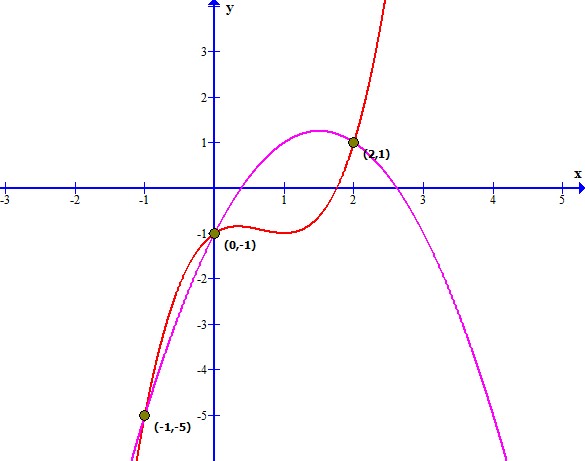
figura 4.4.17 — Figura 1. Representación gráfica de las funciones «f(x)=x^3-2x^2+x-1» y «g(x)=3x-x^2-1».

En el intervalo cerrado $[-1,0]$ , $f(x) \ge g(x)$ mientras que en $[0,2]$ , $g(x) \ge f(x)$ . Luego, se requerirán dos integrales para determinar el área total, por lo que, una parte se calculará un área desde $[-1,0]$ y la otra se calculará desde $[0,2]$ . Para el intervalo $[-1,0]$ , se tomará la fórmula (en el eje $x$ )

$\displaystyle A_1 = \int_a^c{[f(x)-g(x)] \, dx} = \int_{-1}^0{[f(x)-g(x)] \, dx}$

Y para el intervalo $[0,2]$ , la fórmula (en el eje $x$ ) es

$\displaystyle A_2 = \int_c^b{[g(x)-f(x)] \, dx} = \int_0^2{[g(x)-f(x)] \, dx}$

Entonces

$\displaystyle \text{Area} =A_1+A_2$

$\displaystyle \text{Area} = \int_a^c{[f(x)-g(x)] \, dx} + \int_c^b{[g(x)-f(x)] \, dx}$

$\displaystyle \text{Area} = \int_{-1}^0{[f(x)-g(x)] \, dx} + \int_0^2{[g(x)-f(x)] \, dx}$

$\displaystyle \text{Area} = \int_{-1}^0{[(x^3-2x^2+x-1)-(3x-x^2-1)] \, dx} + \int_0^2{[(3x-x^2-1)-(x^3-2x^2+x-1)] \, dx}$

$\displaystyle \text{Area} = \int_{-1}^0{(x^3-x^2-2x) \, dx} + \int_0^2{(-x^3+x^2+2x) \, dx}$

$\displaystyle \text{Area} = \left[\frac{1}{4} x^4 - \frac{1}{3} x^3 - x^2 \right]_{-1}^0 + \left[-\frac{1}{4} x^4 + \frac{1}{3} x^3 + x^2 \right]_0^2$

$\displaystyle \text{Area} = \left\{\left[\frac{1}{4} (0)^4 - \frac{1}{3} (0)^3 - (0)^2 \right] - \left[\frac{1}{4} (-1)^4 - \frac{1}{3} (-1)^3 - (-1)^2 \right]\right\} + \left\{\left[-\frac{1}{4} (2)^4 + \frac{1}{3} (2)^3 + (2)^2 \right] - \left[-\frac{1}{4} (0)^4 + \frac{1}{3} (0)^3 + (0)^2 \right]\right\}$

$\displaystyle \text{Area}= \left(-\frac{1}{4}-\frac{1}{3}+1\right)+\left(-\frac{16}{4}+\frac{8}{3}+4\right) = -\frac{1}{4} - \frac{1}{3} + 1 + \frac{8}{3} = \frac{37}{12}$

Finalmente

$\displaystyle \therefore \text{Area} = \frac{37}{12} \ \text{u}^2 \approx 3.083 \ \text{u}^2$

Problema 2. Calcular el área de la región acotada por las curvas $f(x) = x^3 - 6x^2 + 8x$ y $g(x) = x^2 - 4x$ .

Solución. Primero se determinan los puntos de intersección de ambas curvas dadas, partiendo de la condición f(x)≥g(x). Entonces

$f(x) = g(x)$

$x^3 - 6x^2 + 8x = x^2 - 4x$

$x^3 - 7x^2 + 12x = 0$

$x(x^2 - 7x + 12) = 0$

$x (x - 3)(x - 4)=0$

Los valores de $x$ son $x=0$ , $x=3$ y $x=4$ . Ahora, se realiza la tabulación con las funciones $f(x)$ y $g(x)$ desde $x=0$ hasta $x=4$ con un incremento de 0.5.

Graficando las funciones $f(x)$ y $g(x)$ y localizando los valores de $x$ obtenidos, resulta lo siguiente

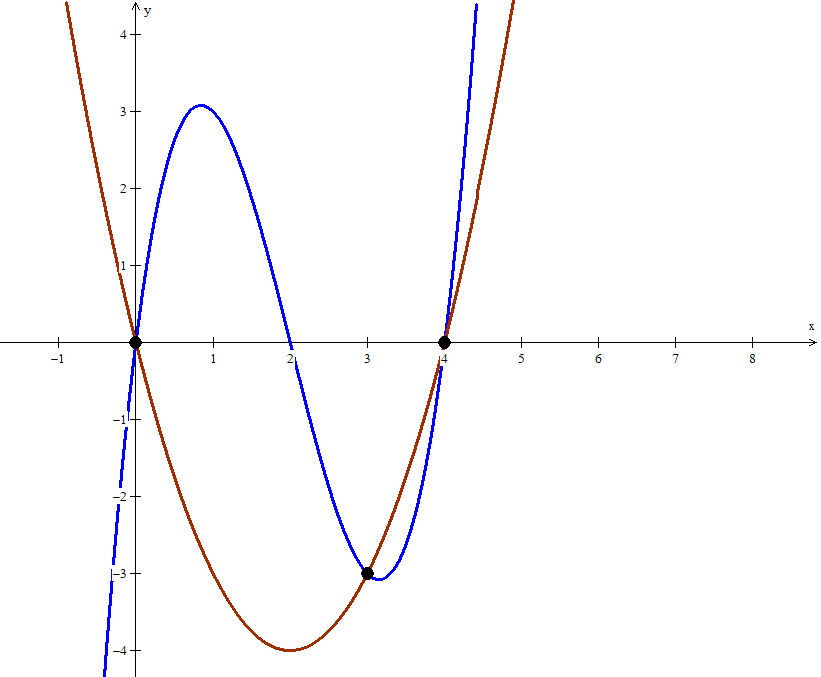
*Figura 2. Representación gráfica de las funciones «f(x)=x^3-6x^2+8x» y «g(x)=x^2-4x».*

Aquí $f(x) \ge g(x)$ para toda $x$ en el intervalo cerrado $[0,3]$ , pero también $g(x) \ge f(x)$ para toda $x$ en el intervalo cerrado $[3,4]$ .

Por lo anterior, se requieren dos integrales para hallar el área total, es decir, una integral para el intervalo $[0,3]$ y otra para el intervalo $[3,4]$ . Para el intervalo $[0,3]$ , se tomará la fórmula (en el eje $x$ )

$\displaystyle A_1 = \int_a^c{[f(x)-g(x)] \, dx} = \int_0^3{[f(x)-g(x)] \, dx}$

Y para el intervalo $[3,4]$ , la fórmula (en el eje $x$ ) es

$\displaystyle A_2 = \int_c^b{[g(x)-f(x)] \, dx} = \int_3^4{[g(x)-f(x)] \, dx}$

Entonces

$\displaystyle \text{Area} =A_1+A_2$

$\displaystyle \text{Area} = \int_a^c{[f(x)-g(x)] \, dx} + \int_c^b{[g(x)-f(x)] \, dx}$

$\displaystyle \text{Area} = \int_0^3{[f(x)-g(x)] \, dx} + \int_3^4{[g(x)-f(x)] \, dx}$

$\displaystyle \text{Area} = \int_0^3{[(x^3-6x^2+8x)-(x^2-4x)] \, dx} + \int_3^4{[(x^2-4x)-(x^3-6x^2+8x)] \, dx}$

$\displaystyle \text{Area} = \int_0^3{(x^3-7x^2+12x) \, dx} + \int_3^4{(-x^3 + 7x^2 - 12x) \, dx}$

$\displaystyle \text{Area} = \left[\frac{1}{4} x^4 - \frac{7}{3} x^3 + 6x^2 + C\right]_0^3 + \left[-\frac{1}{4} x^4 + \frac{7}{3} x^2 - 6x^2 + C \right]_3^4$

$\displaystyle \text{Area} = \left[\frac{1}{4} (3)^4 - \frac{7}{3} (3)^3 + 6(3)^2 \right] - \left[\frac{1}{4} (0)^4 - \frac{7}{3} (0)^3 + 6(0)^2 \right] + \left[-\frac{1}{4} (4)^4 + \frac{7}{3} (4)^3 - 6(4)^2 \right] - \left[-\frac{1}{4} (3)^4 + \frac{7}{3} (3)^2 - 6(3)^2 \right]$

$\displaystyle \text{Area} = \left[\frac{1}{4} (81) - \frac{7}{3} (27) + 6(9) \right] - \left[\frac{1}{4} (0) - \frac{7}{3} (0) + 6(0) \right] + \left[-\frac{1}{4} (256) + \frac{7}{3} (64) - 6(16) \right] - \left[-\frac{1}{4} (81) + \frac{7}{3} (27) - 6(9) \right]$

$\displaystyle \text{Area} = \left(\frac{81}{4} - \frac{189}{3} + 54 \right) - (0) + \left(-\frac{256}{4} + \frac{448}{3} - 96 \right) - \left(-\frac{81}{4} + \frac{189}{3} - 54 \right)$

$\displaystyle \text{Area} = \left(\frac{81}{4} - 63 + 54 \right) + \left(-64 + \frac{448}{3} - 96 \right) - \left(-\frac{81}{4} + 63 - 54 \right)$

$\displaystyle \text{Area} = \left(\frac{81}{4} - 9 \right) + \left(\frac{448}{3} - 160 \right) - \left(-\frac{81}{4} + 9 \right) = \frac{81}{4} - 9 + \frac{448}{3} - 160 + \frac{81}{4} - 9$

$\displaystyle \text{Area} = \frac{1139}{6} - 178 = \frac{71}{6}$

Finalmente

$\displaystyle \therefore \text{Area} = \frac{71}{6} \ \text{u}^2 \approx 11.833 \ \text{u}^2$

$x$	-1	-0.5	0	0.5	1	1.5	2
$f(x)$	-5	-2.125	-1	-0.875	-1	-0.625	1
$g(x)$	-5	-2.75	-1	0.25	1	1.25	1

Área limitada por dos curvas al intersecarse en más de dos puntos. Cálculo integral.

Introducción

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

$x$	1	2	3	3.5	4
$f(x)$	3	0	-3	-2.625	0
$g(x)$	-3	-4	-3	-1.75	0

Área limitada por dos curvas al intersecarse en más de dos puntos. Cálculo integral.

Introducción

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta