Introducción
Considerando la región acotada por las dos curvas y
y las dos rectas
y
y suponiendo que las dos funciones son continuas en el intervalo cerrado
y que
) para toda
en
se tiene la siguiente gráfica (figura 1 y 2).
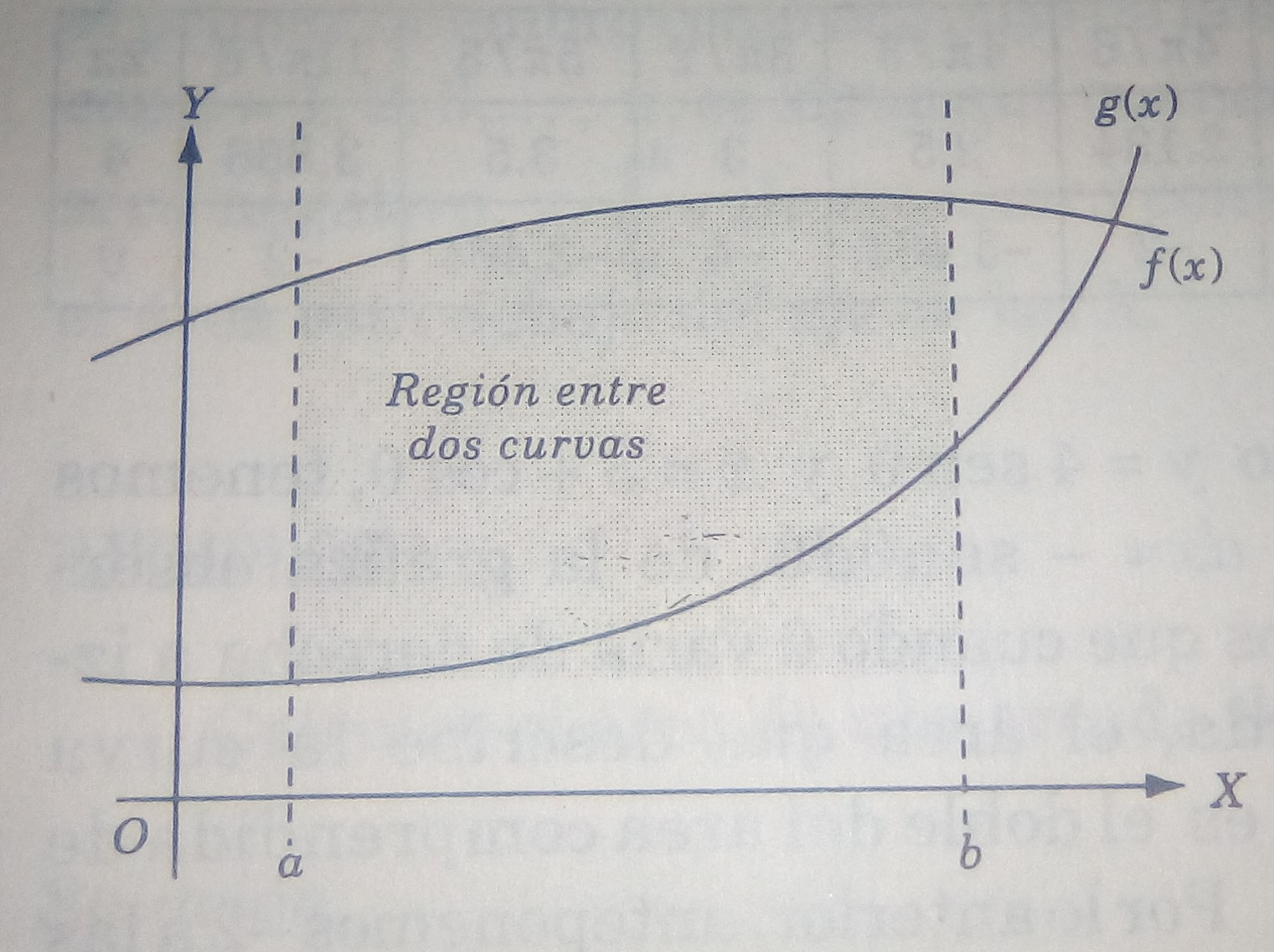
Figura 1. 
Figura 2.
Al dividir el intervalo cerrado en
subintervalos de la longitud
cada uno, y trazando un rectángulo representativo de anchura
y con altura
, donde
está en el i-ésimo subintervalo, se tiene lo siguiente

Figura 3. 
Figura 4. 
Figura 5.
El área del rectángulo representativo es
La suma de las áreas de los rectángulos en la gráfica es
Por tanto, el área de la región comprendida ente dos curvas es
Si y
están por encima del eje
se puede interpretar el área de la región comprendida entre sus gráficas simplemente como el área bajo
menos el área bajo
.
Es necesario aclarar que, por lo general, para determinar el área entre dos curvas hay que aplicar, para rectángulos verticales, la siguiente fórmula (en la variable ):
Para rectángulos horizontales, la siguiente fórmula (en la variable ):
Aquí ,
son o bien puntos adyacentes de intersección de las curvas o puntos sobre ciertas líneas del contorno.
Problemas resueltos
Problema 1. Calcular el área de la región que está acotada por las dos curvas y
y las dos rectas
y
.
Solución. Realizando la tabulación de ambas curvas
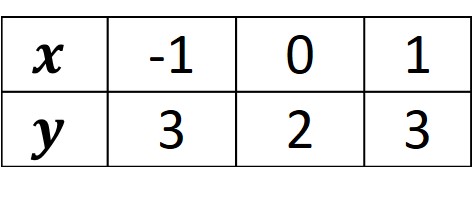
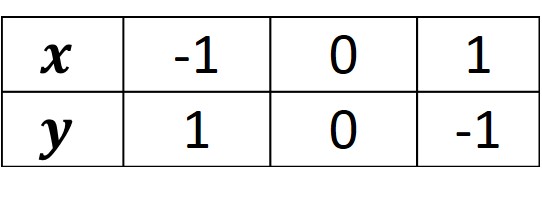
Graficando y localizando el área a determinar

Se tomará y
, para que se cumpla con la condición
para toda
en el intervalo cerrado
.
Aplicando la fórmula para el área entre dos curvas
Resolviéndolo como una integral indefinida
Regresando y reemplazando la variable por sus límites correspondientes, resulta
Finalmente
Problema 2. Calcula el área de la región acotada por la recta y la curva
.
Solución. Para determinar el área, es necesario conocer los límites inferior y superior, para ello, se resolverá las ecuaciones dadas por el problema por el método de igualación, con la finalidad de identificar posibles puntos de intersección, y en base a eso, tomarlos como los límites requeridos, y así, conocer el área de la región acotada.
Resolviendo esto por fórmula general
Por tanto, estos valores de , ayudarán a localizar los puntos de intersección. Realizando la tabulación de ambas funciones

Entonces, los puntos de intersección son y
. Graficando las funciones y los puntos de intersección
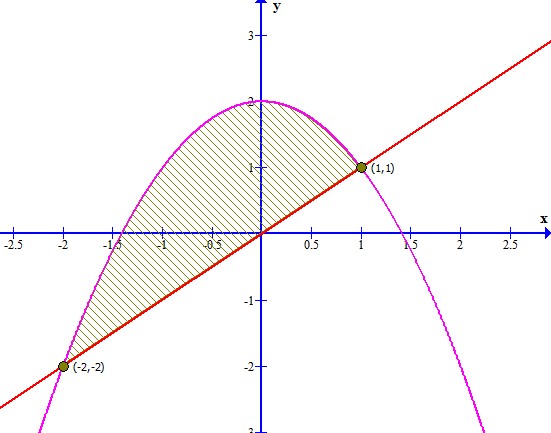
Cuando f(x)≥g(x), la fórmula para calcular el área es
Pero como g(x)≥f(x), la fórmula para calcular el área es
Sustituyendo
Resolviendo la integral
Regresando y reemplazando la variable por sus límites correspondientes, resulta
Finalmente
Problema 3. Calcular el área de la región comprendida entre y
.
Solución. La ecuación se mantendrá mientras que la segunda
se despejará la variable
, es decir, será
. Luego, la condición establecida fue f(x)≥g(x) pero como la variable ahora es
, por tanto, la condición se expresará como f(y)≥g(y). Por tanto, las funciones serán
y
. Partiendo de la nueva condición, se analizará si existen puntos de intersección.
Los valores de son
y
. Después, realizando la tabulación para las funciones
y
, resulta
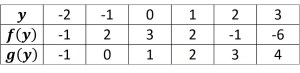
Graficando las funciones

Observando la gráfica, los resultados de la tabulación y los valores de y calculados en base a la nueva condición, existen sólo dos puntos de intersección, que son y
.
El área de la región acotada abarcará desde hasta
. Para este caso, el área se considera en el eje
, por tanto, la fórmula a tomar es
Resolviéndolo como una integral indefinida
Regresando y reemplazando la variable por sus respectivos límites, resulta
Finalmente