Cálculo del volumen de un sólido de revolución. Cálculo integral.

Introducción

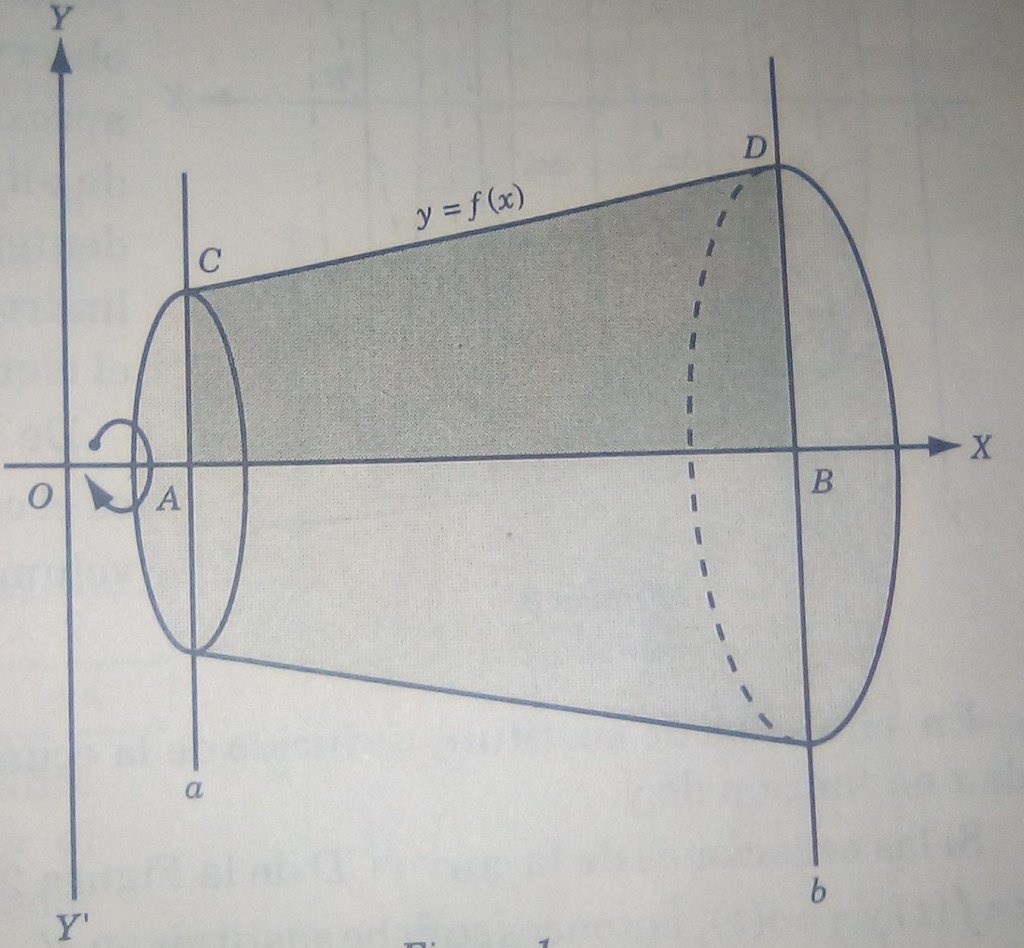
Sea $V$ el volumen del sólido de revolución que se genera haciendo girar una superficie plana $ABCD$ alrededor del eje $x$ , en donde la ecuación de la curva plana $CD$ es $y=f(x)$ (figura 1).

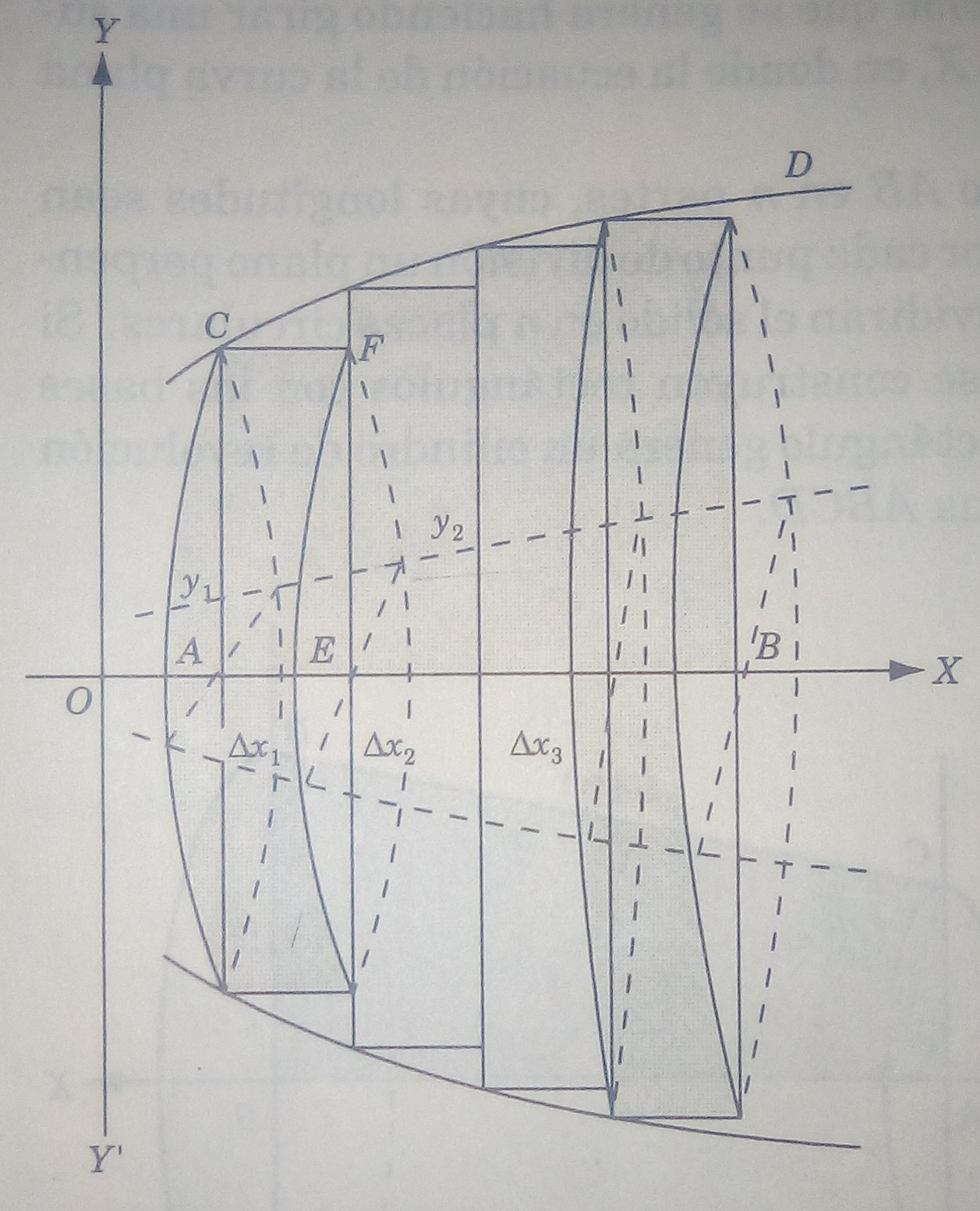
Primer paso. Se divide el segmento $AB$ en $n$ partes, cuyas longitudes sea $\Delta x_1$ , $\Delta x_2$ , $\Delta x_3$ , …, $\Delta x_n$ y se hace pasar por cada punto de división de un plano perpendicular al eje de las $x$ . Dichos planos dividirán el sólido en $n$ placas circulares. Si dentro de la superficie plana $ABCD$ se construyen rectángulos con las bases $\Delta x_1$ , $\Delta x_2$ , $\Delta x_3$ , …, $\Delta x_n$ , entonces en cada rectángulo general un cilindro de revolución cuando se hace girar la superficie plana $ABCD$ .

figura 4.6.1 — Figura 1. Representación gráfica de un volumen del sólido de revolución que se generó al girar una superficie plana.

De esta forma se obtiene un cilindro correspondiente a cada una de las placas circulares. En la figura 4.6.2 se observa que $n=4$ y se muestran los cilindros. El límite de la suma de estos $n$ cilindros ( $n \rightarrow \infty$ ) es el volumen buscado.

Segundo paso. Sean $y_1$ , $y_2$ , $y_3$ , …, $y_n$ las ordenadas de la curva $CD$ en los puntos de división en el eje de las $x$ . Entonces el volumen del cilindro generado por la superficie del rectángulo $AEFC$ es $\pi y_1^2 \Delta x_1$ , y la suma de los volúmenes de todos estos cilindros es

$\displaystyle \pi y_1^2 \Delta x_1 + \pi y_2^2 \Delta x_2 + \pi y_3^2 \Delta x_3 + \cdots + \pi y_n^2 \Delta x_n = \sum_{i=1}^{n}{\pi y_i^2 \Delta x_i}$

Tercer paso. Aplicando el teorema fundamental del cálculo integral (teniendo como límites $OA=a$ y $OB=b$ ), resulta

$\displaystyle \lim_{n \rightarrow \infty}{\sum_{i=1}^{n}{\pi y_i^2 \Delta x_i}} = \int_a^b{\pi y^2 \, dx} = \pi \int_a^b{y^2 \, dx}$

Por lo tanto, el volumen que se genera haciendo girar alrededor del eje de las $x$ la superficie limitada por la curva, el eje de las $x$ y las ordenadas $x=a$ y $x=b$ está dado por la fórmula:

$\displaystyle V_x = \pi \int_a^b{y^2 \, dx}$

En ella se ha de sustituir, deducido de la ecuación de la curva dada, el valor de $y$ en términos de $x$ .

Esta ecuación $\displaystyle V_x = \pi \int_a^b{y^2 \, dx}$ es fácilmente comprensible si se considera una rebanada o placa delgada del sólido formado por dos planos perpendiculares al eje de revolución y se observa que esta placa circula, aproximadamente, como un cilindro de altura $dx$ y base de área $\pi y^2$ . Evidentemente, el volumen de un cilindro tal es $\pi y^2 \, dx$ . Dicho cilindro es el elemento de volumen buscado.

En ella se ha de sustituir, deducido de la ecuación de la curva dada, el valor de $x$ en función de $y$ .

Si las ecuaciones de la curva $CD$ de la figura 2 se dan en forma paramétrica, $x=f(t)$ y $y=\phi (t)$ , entonces se debe sustituir en $\displaystyle V_x = \pi \int_a^b{y^2 \, dx}$ los valores de $y=\phi (t)$ , $dx = f' (t) \, dt$ y cambiar los límites en $t_1$ y $t_2$ . Si $t=t_1$ , cuando $x=a$ , $t=t_2$ cuando $x=0$ .

En conclusión, se puede calcular el volumen de un sólido de revolución mediante las siguientes fórmulas

\displaystyle V_x = \pi \int_a^b{y^2 \, dx}

Problemas resueltos

Problema 1. Calcular el volumen de la esfera que se genera haciendo girar el círculo $x^2+y^2=r^2$ alrededor de un diámetro.

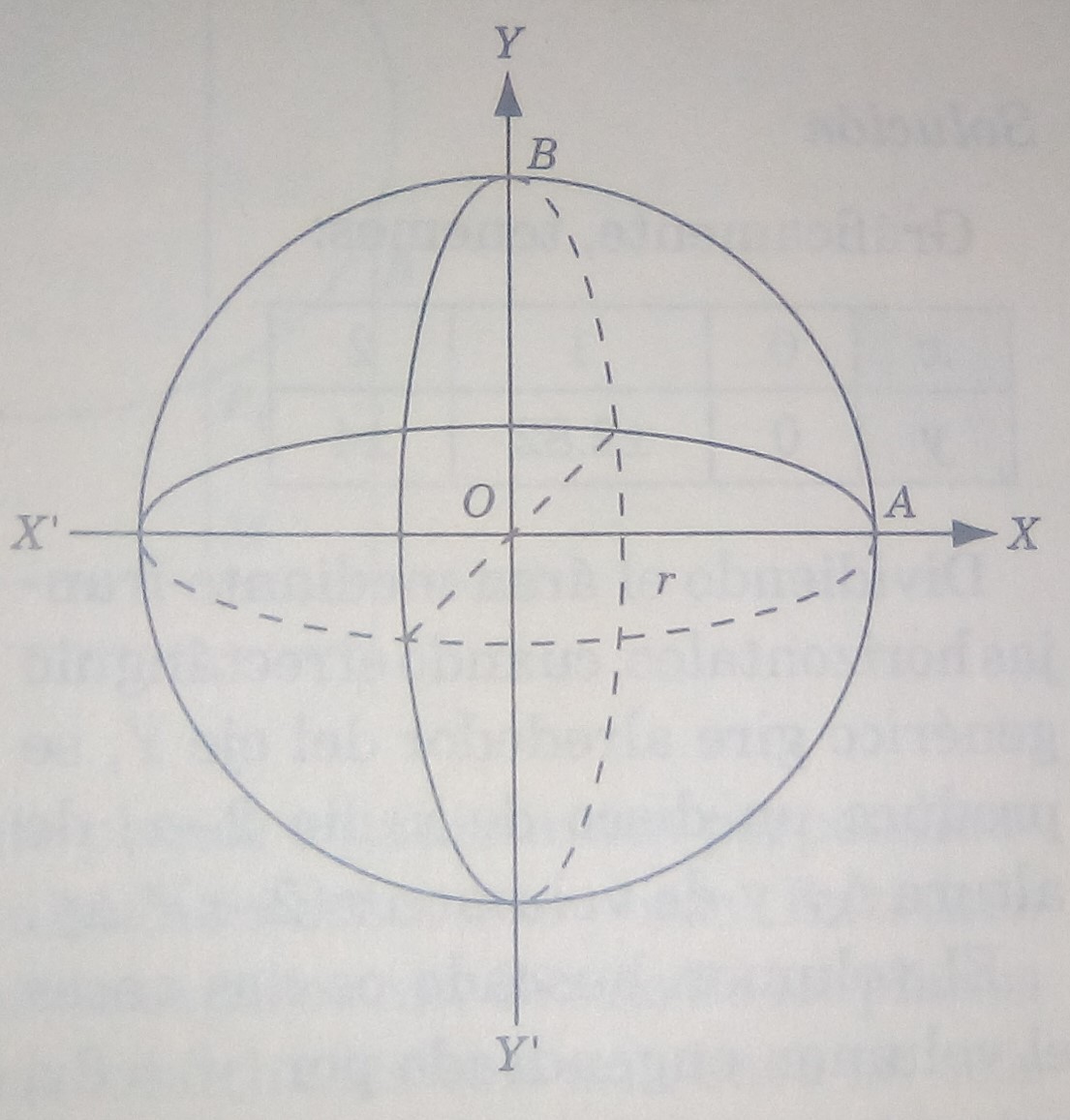
Solución. Despejando el término $y^2$ de la ecuación del círculo, resulta

$x^2+y^2=r^2$

$y^2=r^2-x^2$

Por lo que el volumen buscado es dos veces el volumen engendrado por $OAB$ . Como $OX$ es el eje de revolución, se tiene que

$\displaystyle V_x = \pi \int_a^b{y^2 \, dx} = 2\pi \int_0^r{(r^2-x^2 ) \, dx}$

Resolviéndolo como una integral indefinida

$\displaystyle \int_0^r{(r^2-x^2 ) \, dx} \quad \rightarrow \quad \int{(r^2-x^2 ) \, dx}$

Continuando

$\displaystyle \int{(r^2-x^2 ) \, dx} = r^2 \int{dx} - \int{x^2 \, dx}$

$\displaystyle \int{(r^2-x^2 ) \, dx} = r^2 x - \frac{1}{3} x^3 + C$

Regresando y reemplazando la variable $x$ con sus respectivos limites, resulta

$\displaystyle \int_0^r{(r^2-x^2 ) \, dx} = \left[r^2 x - \frac{1}{3} x^3 + C\right]$

$\displaystyle \int_0^r{(r^2-x^2 ) \, dx} = \left[r^2 (r) - \frac{1}{3} (r)^3 \right] - \left[r^2 (0) - \frac{1}{3} (0)^3 \right]$

$\displaystyle \int_0^r{(r^2-x^2 ) \, dx} = r^3 - \frac{1}{3} r^3 = \frac{2}{3} r^3$

Finalmente

$\displaystyle V_x = 2\pi \int_0^r{(r^2-x^2 ) \, dx}$

$\displaystyle V_x = 2\pi (\frac{2}{3} r^3 )$

$\displaystyle \therefore V_x = \frac{4\pi}{3} r^3 \ \text{u}^3$

Problema 2. Hallar el volumen generado en la rotación del área del primer cuadrante limitada por la parábola $y^2=8x$ y la ordenada correspondiente a $x=2$ con respecto al eje $x$ .

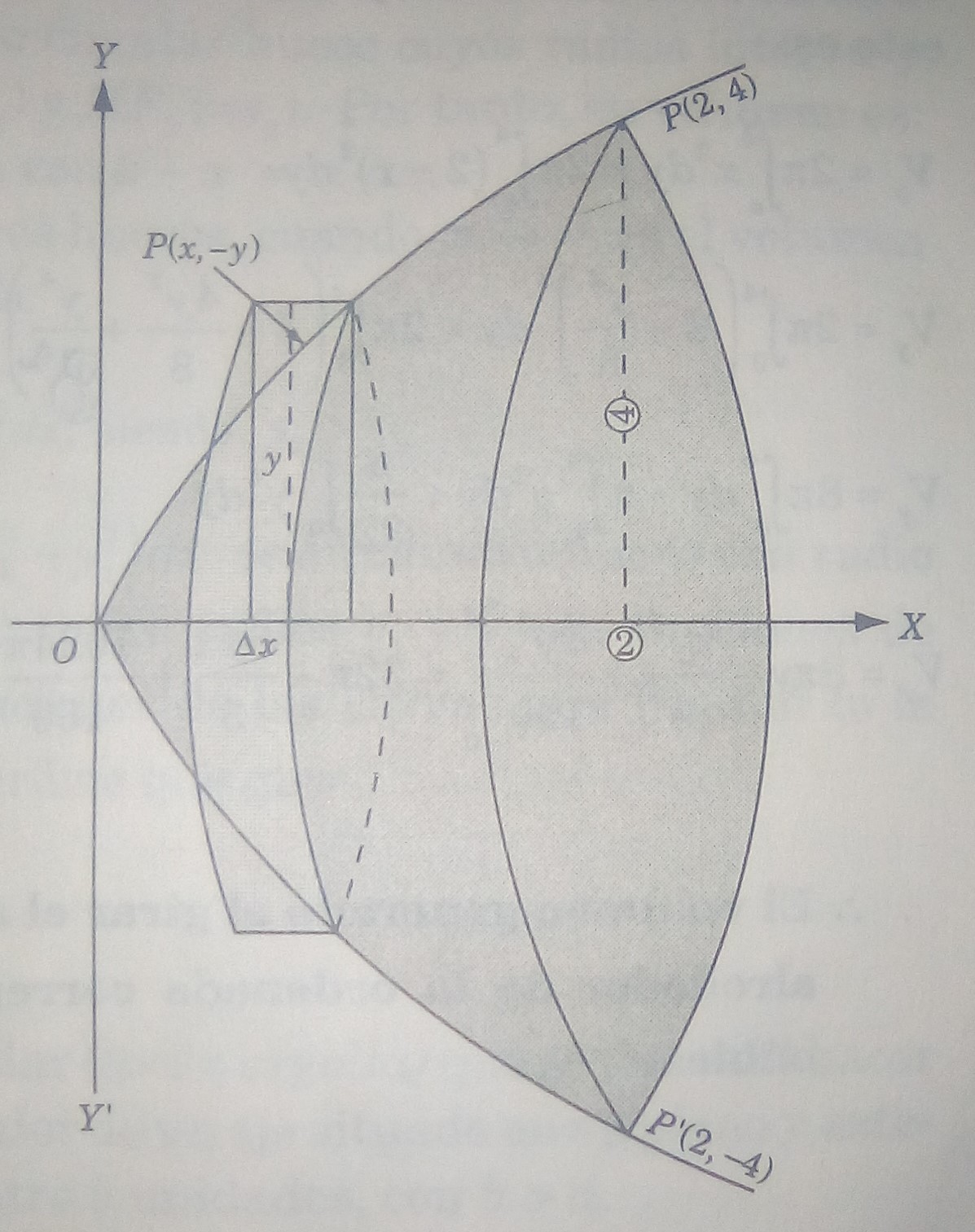
Solución. Despejando la variable $y$ se tiene lo siguiente

$y^2=8x$

$\displaystyle y = \pm \sqrt{8x}$

Realizando la tabulación desde $x=0$ hasta $x=2$ , se tiene que

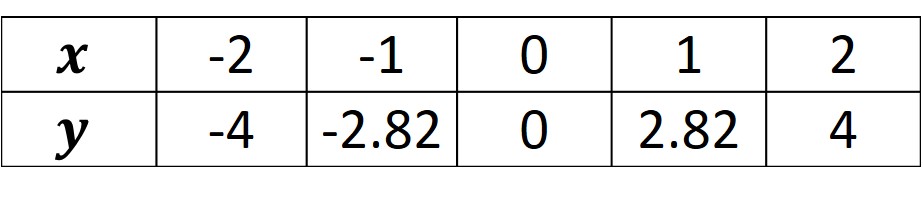
Graficando la función

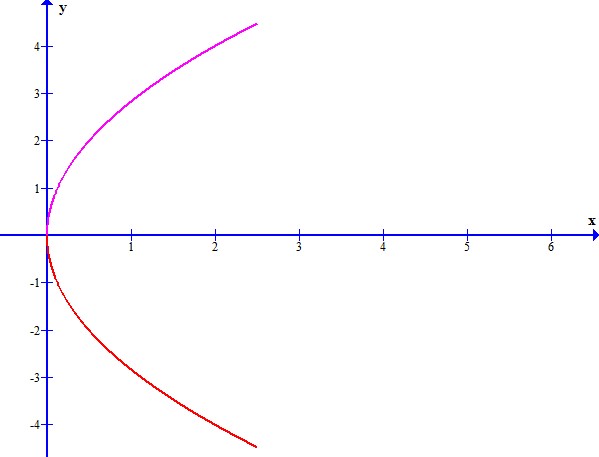
Se divide el área mediante franjas verticales; cuando el rectángulo genérico gire alrededor del eje $x$ se produce un disco de radio $y$ , de altura $\Delta x$ y de volumen $\pi y^2 \, \Delta x$ . La suma de los volúmenes de los $n$ discos, correspondientes a los $n$ rectángulos, resulta ser el volumen pedido.

$\displaystyle V_x = \pi \int_a^b{y^2 \, dx} = \pi \int_0^2{8x \, dx} = 8\pi \int_0^2{x \, dx}$

Resolviéndolo como una integral indefinida

$\displaystyle \int_0^2{x \, dx} \quad \rightarrow \quad \int{x \ dx}$

Continuando

$\displaystyle \int{x \ dx} = \frac{1}{2} x^2 + C$

Añadiendo los límites y evaluando, resulta

$\displaystyle \int_0^2{x \ dx} = \left[\frac{1}{2} x^2 + C \right]_0^2$

$\displaystyle \int_0^2{x \ dx} = \frac{1}{2} (2)^2 - \frac{1}{2} (0)^2 = 2$

Finalmente

$\displaystyle V_x = 8\pi \int_0^2{x \, dx}$

$\displaystyle V_x = 8\pi (2) = 16\pi$

$\displaystyle \therefore V_x = 16 \pi \ \text{u}^3$

Problema 3. Hallar el volumen que se genera al girar el área limitada por la parábola $y^2=8x$ alrededor de la ordenada correspondiente a $x=2$ .

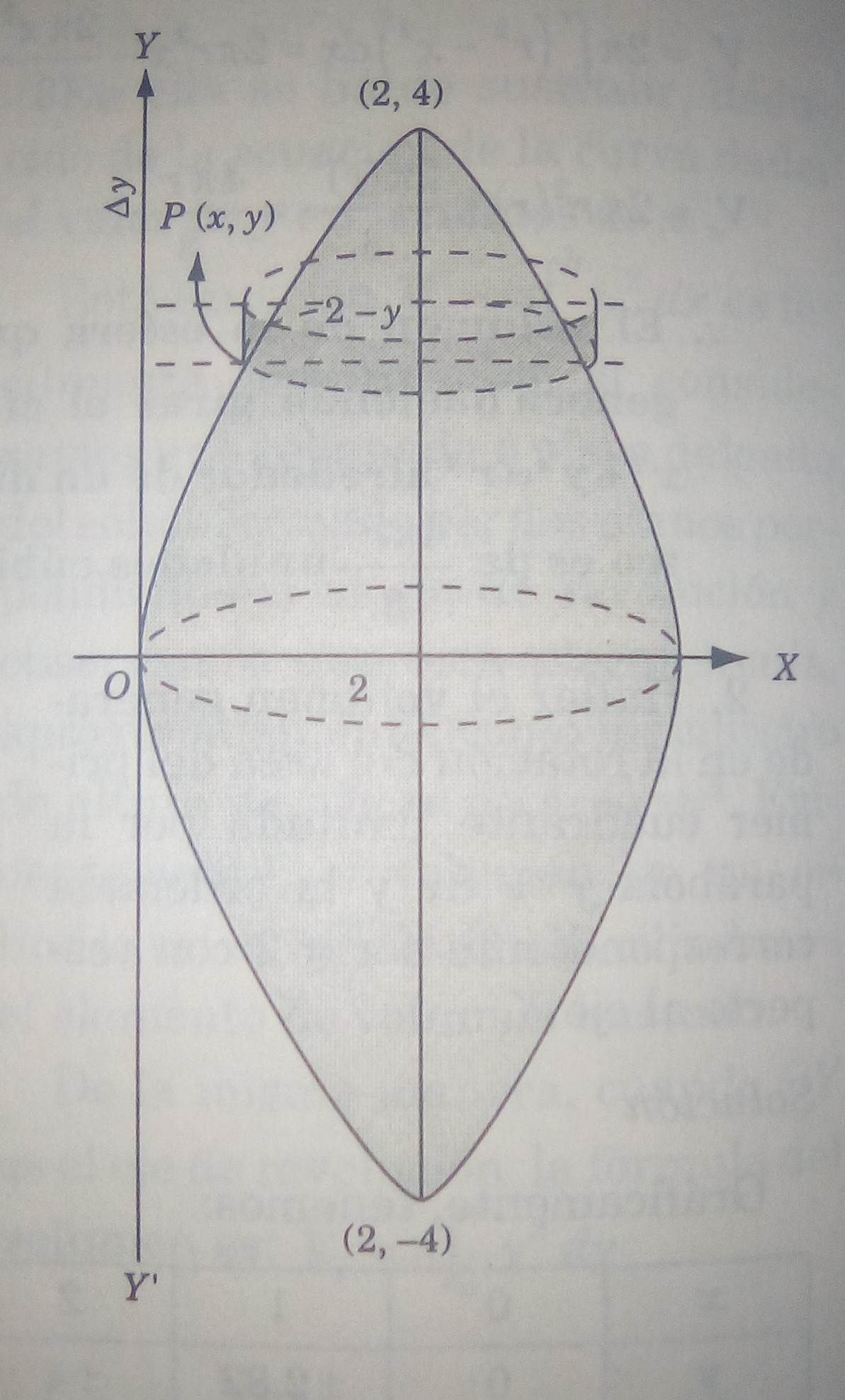
Solución. Realizando la tabulación desde $x=-2$ hasta $x=2$ , se tiene lo siguiente

Dividiendo el área mediante franjas horizontales, cuando el rectángulo genérico gire alrededor del eje $y$ , se produce un disco de radio $2-x$ , de altura $\Delta y$ y de volumen $\pi(2-x)^2 \, \Delta y$ .

El volumen buscado es dos veces el volumen engendrado por $y^2=8x$ , esto es

$\displaystyle V_y = \pi \int_c^d{x^2 \, dy} = 2\pi \int_0^4{(2-x)^2 \, dy}$

Recordando la ecuación de la parábola, se despeja $x$ ( $\displaystyle x = \frac{y^2}{8}$ ). Así que la ecuación del volumen tiene la siguiente expresión

$\displaystyle V_y = 2\pi \int_0^4{(2-x)^2 \, dy} = 2\pi \int_0^4{\left(2- \frac{y^2}{8} \right)^2 \, dy}$

Resolviéndolo como una integral indefinida

$\displaystyle \int_0^4{\left(2- \frac{y^2}{8} \right) \, dy} \quad \rightarrow \quad \int{\left(2- \frac{y^2}{8} \right) \, dy}$

Continuando

$\displaystyle \int{\left(2-\frac{y^2}{8} \right)^2 \, dy} = \int{\left(4 - \frac{1}{2} y^2 + \frac{1}{64} y^4 \right) \, dy}$

$\displaystyle \int{\left(2-\frac{y^2}{8} \right)^2 \, dy} = 4 \int{dy} - \frac{1}{2} \int{y^2 \ dy} + \frac{1}{64} \int{y^4 \ dy}$

$\displaystyle \int{\left(2-\frac{y^2}{8} \right)^2 \, dy} = 4y - \frac{1}{6} y^3 + \frac{1}{320} y^5 + C$

Ahora, añadiendo los límites de integración y evaluando, resulta que

$\displaystyle \int_0^4{\left(2-\frac{y^2}{8} \right)^2 \, dy} = \left[4y - \frac{1}{6} y^3 + \frac{1}{320} y^5 + C\right]_0^4$

$\displaystyle \int_0^4{\left(2-\frac{y^2}{8} \right)^2 \, dy} = \left[4(4) - \frac{1}{6} (4)^3 + \frac{1}{320} (4)^5 \right] - \left[ 4(0) - \frac{1}{6} (0)^3 + \frac{1}{320} (0)^5 \right]$