Introducción al teorema de Thévenin y Norton. Circuitos eléctricos.

Introducción

Se tiene un circuito y se desea encontrar la corriente, el voltaje o la potencia que se entrega a uno de los resistores de la red, que se denomina carga. El teorema de Thévenin establece que la red entera, sin incluir la carga, puede sustituirse por un circuito equivalente con una fuente de voltaje de independiente en serie con un resistor, de tal modo que la relación corriente/voltaje en la carga no cambia. El teorema de Norton es idéntico al anterior, excepto porque el circuito equivalente se forma con una fuente de corriente independiente en paralelo con su resistor.

Para desarrollar estos teorema se supone que el circuito de la figura 1 puede dividirse en dos partes, como se observa en la figura 2. En general, el circuito B es la carga, y puede ser lineal o no lineal. El circuito A es el resto de la red original sin incluir la carga y debe ser lineal. Como tal, el circuito A puede incluir fuentes independientes, fuentes dependientes y resistores, o cualquier otro elemento lineal. Sin embargo, se requiere que en el mismo circuito aparezcan tanto la fuente dependiente como su variable de control.

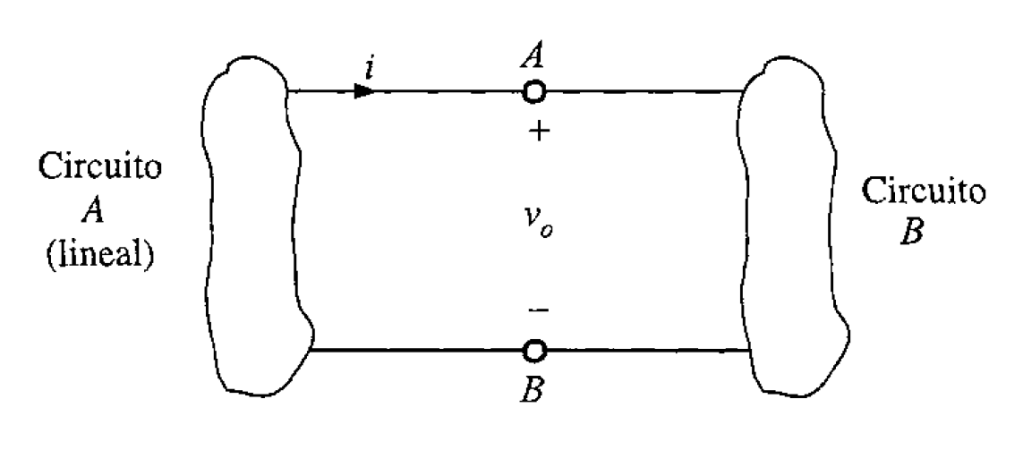
El circuito A entrega una corriente $i$ al circuito B, produciendo un voltaje $v_o$ entre las terminales de entrada del circuito B. Desde el punto de vista de las relaciones de terminal del circuito A, es posible sustituir el circuito B con una fuente de voltaje $v_o$ volts (con la polaridad apropiada), como se muestra en la figura 2. Puesto que el voltaje de terminal no cambia y tampoco lo hace el circuito A, la corriente de terminal $i$ no se modifica.

Aplicando el principio de superposición a la red de la figura 2, se tiene que la corriente total $i$ que se muestra en la figura es la suma de todas las corrientes producidas por todas las fuentes del circuito A y la recién agregada fuente $v_o$ . Entonces, por superposición la corriente $i$ es

donde $i_o$ es la corriente debida a $v_o$ cuando todas las fuentes independientes en el circuito A se hacen cero (esto es, cuando se sustituyen las fuentes de voltajes por cortocircuitos y las fuentes de corriente por circuitos abiertos), e $i_{sc}$ es la corriente de cortocircuito debida a todas las fuentes del circuito A con $v_o$ reemplazada por un cortocircuito.

Los términos $i_o$ y $v_o$ se relacionan por la ecuación

\displaystyle i_o = \frac{-v_o}{R_{\text{Th}}}

donde $R_{Th}$ es la resistencia equivalente del circuito A vista desde las terminales A-B, cuando se anulan todas las fuentes independientes en el circuito A.

Sustituyendo

$\displaystyle i = i_o + i_{sc}$

\displaystyle i = \frac{v_o}{R_{\text{Th}}} + i_{sc}

Esta es una relación general y, por lo tanto, se debe cumplir para cualquier condición específica en las terminales A-B. Como un caso específico, suponga que las terminales está en circuito abierto. Para esta condición $i=0$ y $v_o$ es igual al voltaje de circuito abierto $v_{oc}$ . Por tanto, la ecuación anterior cambia a

\displaystyle 0 = - \frac{v_o}{R_{\text{Th}}} + i_{sc}

Por consiguiente,

\displaystyle v_o = v_{oc} - R_{\text{Th}} i

Esta ecuación establece que el voltaje de circuito abierto es igual a la corriente de cortocircuito multiplicada por la resistencia equivalente del circuito A con todas las fuentes independientes anuladas. $R_{Th}$ se denomina la resistencia equivalente de Thévenin.

$\displaystyle i = \frac{-v_o}{R_{\text{Th}}} + \frac{v_{oc}}{R_{\text{Th}}}$

En la figura 3 muestra el circuito correspondiente a la ecuación (5) lo establece el teorema de Thévenin. La figura 4 muestra el circuito para la ecuación (3). El hecho de que este circuito es equivalente en las terminales A-B al circuito A en la figura 2 lo establece el teorema de Norton.

Figura 3. Circuito equivalente de Thévenin.

Figura 4. Circuito equivalente de Norton.

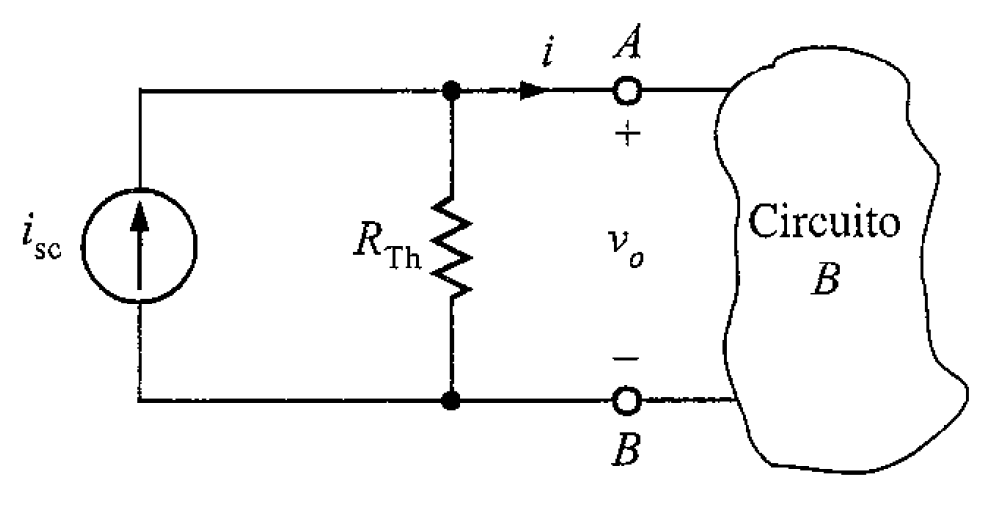
Las relaciones especificadas en las figuras 3 y 4 y la ecuación (5) tiene un significado adicional, ya que representan lo que se denomina transformación o intercambio de fuentes. Estas relaciones indican que si una red incluye una fuente de corriente $i$ en paralelo con un resistor $R$ , es posible sustituir esta combinación con una fuente de voltaje con valor $v= Ri$ en serie con el resistor $R$ . También se cumple lo inverso; esto es, una fuente de voltaje $v$ en serie con un resistor $R$ puede sustituirse por una fuente de corriente de valor $i = v/R$ en paralelo con el resistor $R$ . Los parámetros dentro del circuito (por ejemplo, un voltaje de salida) no cambian bajo estas transformaciones.

Debe hacerse énfasis en que los dos circuitos equivalentes de las figuras 3 y 4 son equivalentes sólo en los dos nodos externos. Por ejemplo, si se desconecta el circuito B en ambas redes de las figuras 3 y 4, el circuito de la figura 4 disipa potencia, mientras que el de la figura 3 no lo hace.

Problema resuelto

Problema 1. Encontrar $V_o$ en el circuito de la figura 5.

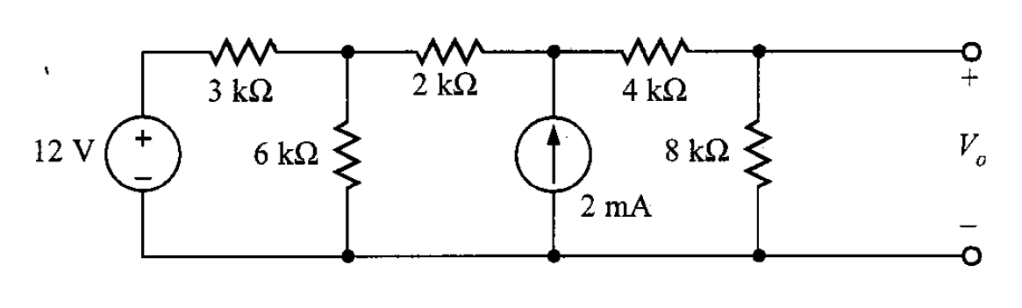
Solución. Si se comienza el análisis por el extremo izquierdo de la red de la figura 1, la combinación en serie de la fuente de 12 V y el resistor de 3 kΩ se convierte en una fuente de corriente de

$\displaystyle \frac{12}{3 \ \text{k}} = \frac{12}{3} \times 10^{-3} = 4 \ \text{mA}$

en paralelo con dicho resistor. Y en los resistores de 3 kΩ y de 6 kΩ se reducen ya que están en paralelo.

$\displaystyle \frac{1}{R_{P1}} = \frac{1}{3 \ \text{k}} + \frac{1}{6 \ \text{k}} \quad \rightarrow \quad R_{P1} = 2 \ \text{k} \Omega$

En la figura 6, se muestra la transformación de fuentes.

Ahora, se observa que la fuente de corriente de 4 mA y la resistencia de 2 kΩ se convierten en una fuente de

$\displaystyle (4 \ \text{m})(2 \ \text{k}) = (4 \times 10^{-3})(2 \times 10^3) = 8 \ \text{V}$

en serie con el mismo resistor; también los dos resistores de 2 kΩ están en serie.

$R_{S1} = 2 \ \text{k} + 2 \ \text{k} = 4 \ \text{k} \Omega$

Con estos resultados, se tiene la segunda reducción del circuito (figura 7).

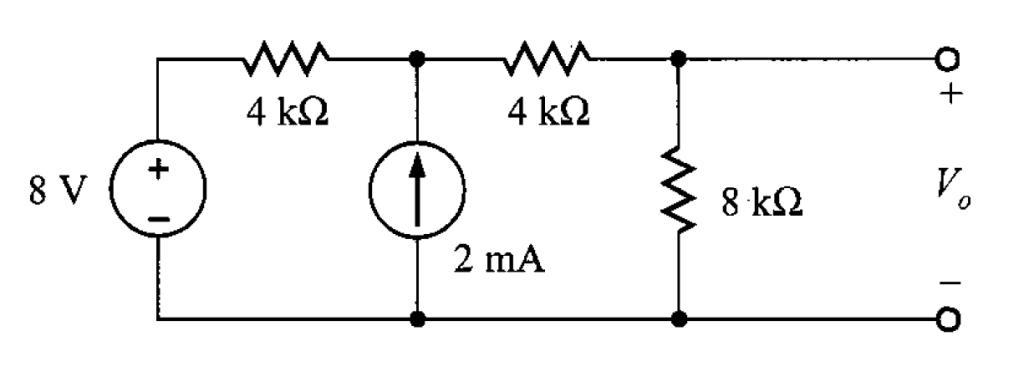
Ahora, si se convierte la combinación de la fuente de 8 V y el resistor de 4 kΩ en una fuente de

$\displaystyle \frac{8}{4 \ \text{k}} = \frac{8}{4 \times 10^3} = 2 \times 10^{-3} = 2 \ \text{mA}$

Con esta nueva fuente de 2 mA estará en paralelo con el resistor de 4 kΩ y con la fuente de corriente de 2 mA (figura 8).

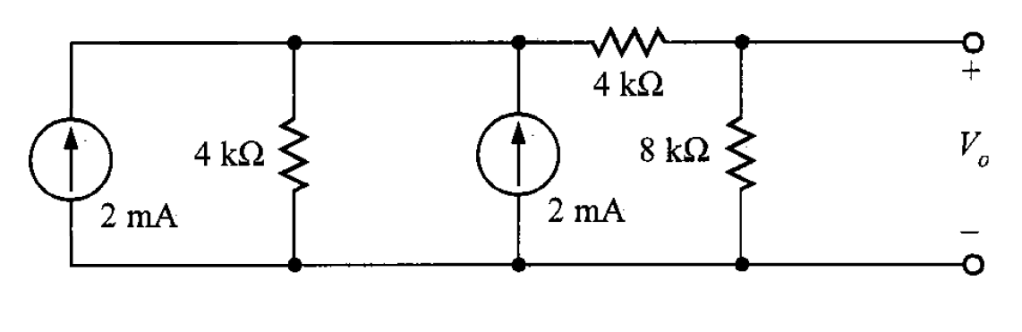
Sumando las fuentes de corrientes, resulta

$\displaystyle 2 \ \text{m} + 2 \ \text{m} = 4 \ \text{mA}$

En la figura 9 se ilustra la reducción de las fuentes de corriente

Para obtener el valor de $V_o$ primero debe calcularse $I_o$ . Por división de corriente, el valor de $I_o$ es

$\displaystyle I_o = \left[ \frac{4 \ \text{k}}{4 \ \text{k} + (4 \ \text{k} + 8 \ \text{k})} \right] (4 \ \text{m})$

$\displaystyle I_o = \left( \frac{4 \ \text{k}}{16 \ \text{k}} \right) (4 \ \text{m})$

$\displaystyle I_o = \left( \frac{1}{4} \right) (4 \ \text{m}) = 1 \ \text{m}$

$\displaystyle I_o = 1 \ \text{mA}$

Finalmente, el valor de $V_o$ es

$\displaystyle V_o = (8 \ \text{k}) I_o$

$\displaystyle V_o = (8 \ \text{k}) (1 \ \text{m}) = (8 \times 10^3)(1 \times 10^{-3})$

$\displaystyle \therefore V_o = 8 \ \text{V}$

Introducción al teorema de Thévenin y Norton. Circuitos eléctricos.

Introducción

Problema resuelto

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Introducción al teorema de Thévenin y Norton. Circuitos eléctricos.

Introducción

Problema resuelto

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta