Momento para un sistema lineal y un sistema bidimensional. Cálculo integral.

Momento para un sistema lineal

El momento que produce una cierta masa respecto del punto $E$ se define así:

$\text{Momento} = (\text{masa})(\text{brazo del momento})$

Aquí el brazo del momento es la distancia de la masa hasta el punto $E$ .

Un ejemplo básico, se supondrá que en un columpio un niño $A$ de 24 kg de peso se sienta 2.5 m a la izquierda del centro de apoyo $E$ y el otro niño $B$ , de 30 kg, se sienta 2.5 m a la derecha de $E$ (figura 1).

Observando la imagen, se deduce que el columpio comenzará a girar en un plano no vertical, es decir, de acuerdo con el giro de las manecillas del reloj en torno al punto $E$ . Esto se debe a que el niño $A$ de la izquierda tiene un peso menor que el niño $B$ de la derecha.

Para que el columpio se encuentre en equilibrio, es necesario que ambos momentos sean iguales. Entonces, si el niño $B$ de 30 kg se sienta a 2 m de distancia de $E$ , en ese instante se nivelará el columpio, ya que:

Si se ubica el origen $O$ en $E$ y se definen las coordenadas $x_1=-2.5$ y $x_2=2$ , el columpio quedará en equilibrio, debido a que el momento total resultante de ambas masas es nulo respecto del origen. En otras palabras

Momento en O $= m_1 x_1 + m_2 x_2$

Momento en O $= (24)(-2.5)+(30)(2)=-60+60$

Momento en O $=0$

De manera general, suponiendo que varias masas $m_1$ , $m_2$ , $m_3$ , …, $m_n$ , colocados a lo largo del eje $x$ en los puntos respectivos $x_1$ , $x_2$ , $x_3$ , …, $x_n$ (figura 2).

En tal situación la medida de la tendencia del sistema a girar alrededor del origen $O$ se denomina momento del sistema respecto del origen, y se representa como

$M_o=m_1 x_1+m_2 x_2+m_3 x_3+ \cdots +m_n x_n$

$\displaystyle M_o = \sum_{i=1}^{n}{m_i x_i}$

Si el momento es igual a cero, se dice que el sistema está en equilibrio.

Ahora, al considerar un sistema que no está en equilibrio y al mover el punto de apoyo a un cierto $x=\overline{x}$ de modo que el sistema ya permanezca en equilibrio, lo anterior da lugar a:

$\displaystyle \sum_{i=1}^n{m_i (x_i - \overline{x})} = m_1 (x_1 - \overline{x} ) + m_2 (x_2 - \overline{x} ) + \cdots +m_n (x_n - \overline{x} ) = 0$

Es decir

$\displaystyle \sum_{i=1}^n{m_i x_i} - \sum_{i=1}^n{m_i \overline{x}} = 0$

Despejando $\overline{x}$

$\displaystyle \overline{x} = \frac{\sum_{i=1}^n{m_i x_i}}{\sum_{i=1}^n{m_i}} = \frac{M_o}{m}$

Donde $M_o$ es el momento del sistema respecto del origen y $m$ es la masa total del sistema.

Al punto $\overline{x}$ de equilibrio se le denomina centro de masa o centro de gravedad del sistema.

Problemas resueltos

Problema 1. Hallar el centro de gravedad para el siguiente sistema lineal: $m_1=16$ , $x_1=-7$ ; $m_2=19$ , $x_2=3$ ; $m_3=11$ , $x_3=8$ ; $m_4=14$ , $x_4=10.5$ .

Solución. Se determina el momento el sistema respecto del origen

$\displaystyle M_o = \sum_{i=1}^4{m_i x_i} = m_1 x_1+m_2 x_2+m_3 x_3+m_4 x_4$

$\displaystyle M_o = (16)(-7)+(19)(3)+(11)(8)+(14)(10.5)$

$\displaystyle M_o=-112+57+88+147$

$\displaystyle M_o = 180 \ \text{kg m}$

Después, se calcula la masa total del sistema

$\displaystyle m = \sum_{i=1}^4{m_i} = m_1+m_2+m_3+m_4$

$m=16+19+11+14$

$m=60 \ \text{kg}$

Por último, utilizando la fórmula del centro de masa

$\displaystyle \overline{x} = \frac{M_o}{m}$

$\displaystyle \overline{x} = \frac{180 \ \text{kg m}}{60 \ \text{kg}}$

$\displaystyle \overline{x} = 3 \ \text{m}$

Finalmente, el centro de masa del sistema dado es de 3 m.

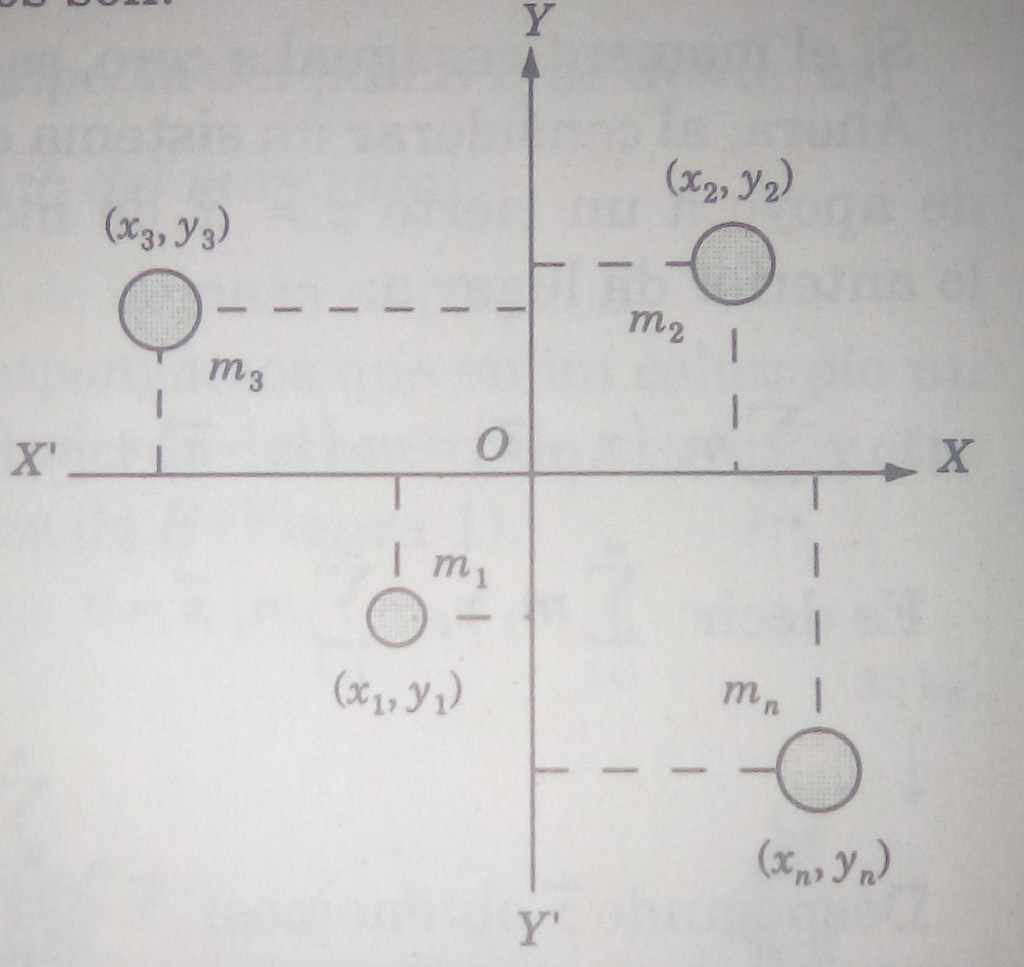
Momento para un sistema bidimensional

Considerando las masas $m_1$ , $m_2$ , $m_3$ , …, $m_n$ , colocadas en un plano cartesiano sobre los puntos $(x_1,y_1 )$ , $(x_2,y_2 )$ , $(x_3,y_3 )$ , …, $(x_n,y_n )$ , respectivamente (figura 4.8.3). Para tal sistema, se tiene que sus momentos son

Momento $M_x$ respecto al eje $x$

$\displaystyle M_x=m_1 y_1+m_2 y_2+m_3 y_3+ \cdots +m_n y_n = \sum_{i=1}^n{m_i y_i}$

Momento $M_y$ respecto al eje $y$

$\displaystyle M_y = m_1 x_1+m_2 x_2+m_3 x_3+ \cdots +m_n x_n = \sum_{i=1}^n{m_i x_i}$

La masa total del sistema es

$\displaystyle m=m_1+m_2+m_3+ \cdots +m_n=\sum_{i=1}^n{m_i}$

El centro de masas $(\overline{x},\overline{y} )$ se obtiene con las fórmulas

\displaystyle \overline{x} = \frac{M_y}{m}

\displaystyle \overline{y} = \frac{M_x}{m}

Lo anterior se interpreta como que la masa total $m$ colocada en el centro de masa $(\overline{x} ,\overline{y} )$ producirá los mismos momentos totales $M_x$ , $M_y$ que el sistema en cuestión.

Problemas resueltos

Problema 2. Hallar el centro de masa de un sistema constituido por las masas $m_1=13$ , $m_2=8$ , $m_3=6$ y $m_4=11$ , colocadas en los puntos $(5, -3)$ , $(1, 2)$ , $(-8, 4)$ y $(-4, -7)$ , respectivamente.