Momentos de una superficie. Cálculo integral.

Introducción

Considerando ahora una placa plana de material (lámina o cartón) cuya masa total está distribuida uniformemente por la placa, es decir, su densidad es la misma en todos sus puntos (realmente la placa sería tridimensional, pero se considerará como una superficie). Si se sabe que el punto de equilibrio de una lámina circular es su centro y que el de una superficie rectangular es su centro geométrico, se define el centro de masa $(\overline{x},\overline{y})$ de una lámina como el punto de equilibrio de un sistema finito de partículas.

Considerando la figura 1, se tiene una lámina de densidad constante ρ. El rectángulo representativo se ha obtenido subdividiendo el intervalo cerrado $[a, b]$ en $n$ subintervalos de acuerdo con ∆x; se representa el centro de masa del i-ésimo rectángulo con el punto $(x_i,y_i )$ y aplicando la fórmula del punto medio. Entonces

$\displaystyle y_i = \frac{f(x_i )+g(x_i )}{2}$

La masa del i-ésimo rectángulo es

$\text{masa} = \text{densidad} \cdot \text{area}$

$\text{masa} = \rho \cdot \Delta A_i$

$\displaystyle \text{masa} = \rho \cdot [f(x_i )-g(x_i )]\Delta x$

La masa total de la superficie se puede estimar con

$\displaystyle m = \sum_{i=1}^n{\rho \cdot [f(x_i )-g(x_i )]\Delta x}$

Tomando el límite en ambos miembros, se brinda la definición de masa

$\displaystyle \lim_{n \rightarrow \infty}{m} = \lim_{n \rightarrow \infty}{\sum_{i=1}^n{\rho \cdot [f(x_i )-g(x_i )]\Delta x}}$

$\displaystyle m = \int_a^b{\rho \cdot [f(x)-g(x)]dx}$

$\displaystyle m = \rho \int_a^b{[f(x)-g(x)]dx} = \rho \cdot A = \rho A$

Aquí $A$ es el área de la lámina.

El momento respecto del eje $x$ del i-ésimo rectángulo es

$\text{momento} = (\text{masa})(\text{brazo del momento})$

$\text{momento} = (\rho \Delta A_i )(y_i )$

$\displaystyle \text{momento} = \rho [f(x_i )-g(x_i )]\Delta x \left[\frac{f(x_i )+g(x_i )}{2} \right]$

$\displaystyle \text{momento} = \frac{\rho}{2} \left\{[f(x_i )]^2-[g(x_i )]^2 \right\} \Delta x$

Sumando todos estos momentos y haciendo que n→∞, se obtiene el momento respecto del eje $x$ definido por

$\displaystyle M_x = \int_a^b{\frac{\rho}{2} \left\{[f(x)]^2-[g(x)]^2 \right\} dx}$

$\displaystyle M_x = \frac{\rho}{2} \int_a^b{ \left\{[f(x)]^2-[g(x)]^2 \right\} dx}$

Asimismo, el momento respecto al eje $y$ es

$\displaystyle M_y = \int_a^b{\frac{\rho}{2} x[f(x)-g(x)] dx}$

$\displaystyle M_y = \frac{\rho}{2} \int_a^b{x[f(x)-g(x)] dx}$

Por lo que, el centro de masa es

\displaystyle \overline{x} = \frac{M_y}{m}

\displaystyle \overline{y} = \frac{M_x}{m}

Problemas resueltos

Problema 1. Hallar el centro de masa de la lámina de densidad uniforme ρ limitada por $y=9-x$ y el eje $x$ .

Solución. Se grafica la función.

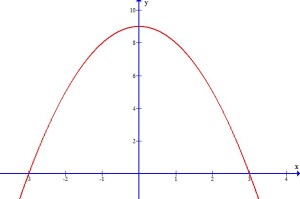
En la figura 2, se tomarán los límites para la integral desde -3 hasta 3. Después, las funciones a considerar son $f(x)=9-x^2$ y $g(x)=0$ . Y sustituyendo en la fórmula para determinar la masa total

$\displaystyle m = \rho \int_a^b{[f(x)-g(x)]dx}$

$\displaystyle m = \rho \int_{-3}^3{[(9-x^2 )-(0)]dx} = \rho \int_{-3}^3{(9-x^2 ) \, dx}$

$\displaystyle m = \rho \left[9x-\frac{1}{3} x^3 \right]_{-3}^3 = \rho \left[9(3)-\frac{1}{3} (3)^3 \right] - \rho \left[9(-3) - \frac{1}{3} {(-3)}^3 \right]$

$\displaystyle m = \rho (27-9) - \rho (-27+9) = 18 \rho + 18 \rho$

$m=36\rho$

Calculando el momento respecto al eje $x$

$\displaystyle M_x = \frac{\rho}{2} \int_a^b{\left\{[f(x)]^2-[g(x)]^2 \right\} \, dx}$

$\displaystyle M_x = \frac{\rho}{2} \int_{-3}^3{ \left[ (9-x^2 )^2-(0)^2 \right] \, dx} = \frac{\rho}{2} \int_{-3}^3{(81-18x^2+x^4 ) \, dx}$

$\displaystyle M_x = \frac{\rho}{2} \left[81x-6x^3 + \frac{1}{5} x^5 \right]_{-3}^3 = \frac{\rho}{2} \left[81(3)-6(3)^3 + \frac{1}{5} (3)^5 \right] - \frac{\rho}{2} \left[ 81(-3)-6(-3)^3+\frac{1}{5} (-3)^5 \right]$

$\displaystyle M_x = \frac{\rho}{2} \left[81(3)-6(27)+\frac{1}{5} (243)\right] - \frac{\rho}{2} \left[81(-3)-6(-27)+\frac{1}{5} (-243)\right]$

$\displaystyle M_x = \frac{\rho}{2} (243-162+\frac{243}{5}) - \frac{\rho}{2} (-243+162-\frac{243}{5}) = \frac{\rho}{2} (\frac{648}{5}) + \frac{\rho}{2} (\frac{648}{5})$

$\displaystyle M_x = \frac{648}{5} \rho$

Calculando el momento respecto al eje $y$

$\displaystyle M_y = \frac{\rho}{2} \int_a^b{x[f(x)-g(x)] \, dx} = \frac{\rho}{2} \int_{-3}^3{x[(9-x^2 )-(0)] \, dx}$

$\displaystyle M_y = \frac{\rho}{2} \int_{-3}^3{x(9-x^2 ) \, dx} = \frac{\rho}{2} \int_{-3}^3{(9x-x^3 ) \, dx} = \frac{\rho}{2} \left[\frac{9}{2} x^2 - \frac{1}{4} x^4 \right]_{-3}^3$

$\displaystyle M_y = \frac{\rho}{2} \left[\frac{9}{2} (3)^2 - \frac{1}{4} (3)^4 \right] - \frac{\rho}{2} \left[\frac{9}{2} (-3)^2 - \frac{1}{4} (-3)^4 \right]$

$\displaystyle M_y = \frac{\rho}{2} \left[\frac{9}{2} (9) - \frac{1}{4} (81)\right] - \frac{\rho}{2} \left[\frac{9}{2} (9) - \frac{1}{4} (81)\right]$

$M_y=0$

Y calculando el centro de masa

\displaystyle \overline{x} = \frac{0}{36 \rho}

Por tanto, el centro de masa es

$\displaystyle \therefore (\overline{x},\overline{y} ) = (0,\frac{18}{5} \rho)$

Nota: se debe tener presente que el centro de masa de una lámina uniforme sólo depende de la forma de ésta, no de su densidad.

En general, si una figura plana tiene un centro de simetría, ese punto es el centro de gravedad. Además, si una figura plana tiene un eje de simetría, el centro de gravedad estará en ese eje.

Generalizando, a la fórmula del centro de masas de una lámina cuando se calcula el centro de una región sin masa del plano se llama centroide o centro de gravedad de esa región. Con base en la figura 3, se observa que la superficie $AMPNB$ que se divide en $n$ rectángulos, cada uno con base $\Delta x$ . Sean $dA$ su área y $C(h,k)$ las coordenadas de su centro de gravedad.

Entonces

$dA=y \, dx$

$h=x$

$\displaystyle k = \frac{1}{2} y$

El momento de la superficie de este rectángulo básico con respecto a $OX$ (también $OY$ ) es el producto de su área por la distancia de su centro de gravedad a $OX$ (también $OY$ ). Si dichos momentos son respectivamente $dM_x$ y $dM_y$ , entonces

El momento de la superficie de la figura $AMPNB$ se obtiene al aplicar el teorema fundamental del cálculo integral a la suma de los momentos de las superficies de los rectángulos fundamentales. De esta manera se tiene los siguiente

\displaystyle \int{dM_x} = \int{k \, dA}

Si $(\overline{x}, \overline{y} )$ son las coordenadas del centro de gravedad de la superficie $AMPNB$ y $A$ es su área, las relaciones entro los momentos de superficie y $\overline{x}$ y $\overline{y}$ se expresan con

Con el fin de calcular $(\overline{x},\overline{y} )$ , se hallarán lo momentos $M_x$ y $M_y$ .

Según $dA=y \, dx$ , $h=x$ , $\displaystyle k = \frac{1}{2}$ y$ y $\displaystyle M_x = \int{k \, dA}$ , $\displaystyle M_y=\int{h \, dA}$ , éstos son, para la superficie $AMPNB$

\displaystyle M_x = \frac{1}{2} \int_a^b{y^2 \, dx}

\displaystyle M_x = \frac{1}{2} \int_a^b{ \left\{ [f(x)]^2-[g(x)]^2 \right\} \, dx}

Donde debe sustituirse el valor de $y$ en función de $x$ deducido por la ecuación de la curva $MPN$ de la figura 4.8.5.

Si se conoce el área $A$ , entonces de $A \overline{x}=M_y$ y $A \overline{y} = M_x$ , se expresa lo siguiente

\displaystyle \overline{x} = \frac{M_y}{A}

\displaystyle \overline{x} = \frac{ \int_a^b{x[f(x)-g(x)] \, dx}}{A}

Si los rectángulos fundamentales de la curva son respecto del eje $y$ , se tiene que $C(h,k)$ , $\displaystyle h=\frac{1}{2} x$ , $y=k$ , $dM_x=k \, dA$ , $dM_y=h \, dA$ , $\displaystyle M_x=\int{k \, dA}$ , $\displaystyle M_y= \int{k \, dA}$ , entonces $\displaystyle A\overline{x} = M_y$ y $\displaystyle A\overline{y}=M_x$ , y

\displaystyle M_x = \int_c^d{[f(y)-g(y)]y \, dy}

Y su centro de gravedad es

\displaystyle \overline{x} = \frac{\int_c^d{[f(y)-g(y)]y \, dy}}{A}

Nota: todo este procedimiento está basado en la condición $f(x) \ge g(x)$ pero si $g(x) \ge f(x)$ sólo basta con invertir las funciones (lo mismo aplica para las funciones $f(y)$ y $g(y)$ ).

Problemas resueltos

Problema 1. Hallar el centro de gravedad de cada una de las superficies limitadas por las siguientes curvas $y=x^2-2x-3$ y $y=6x-x^2-3$ .

Solución. Asignando a $f(x)=x^2-2x-3$ y a $g(x)=6x-x^2-3$ , se grafican ambas funciones.

De ambas funciones, se observa que $g(x) > f(x)$ . Después, se determinan los valores de $x$ en donde las funciones presentan puntos de intersección.

$\displaystyle f(x)=g(x)$

$\displaystyle x^2-2x-3=6x-x^2-3$

$2x^2-8x=0$

$2x(x-4)=0$

Entonces, los valores son $x=0$ y $x=4$ , por tanto, estos valores serán los límites inferior y superior. Luego, calculando el área de la región sombreada resulta

$\displaystyle A = \int_a^b{[f(x)-g(x)] \, dx}$

Pero como $g(x) \ge f(x)$

$\displaystyle A = \int_a^b{[g(x)-f(x)] \, dx}$

Continuando

$\displaystyle A = \int_0^4{[(6x-x^2-3)-(x^2-2x-3)] \, dx}$

$\displaystyle A = \int_0^4{(6x-x^2-3-x^2+2x+3) \, dx} = \int_0^4{(8x-2x^2 ) \, dx}$

$\displaystyle A = \left[4x^2 - \frac{2}{3} x^3 + C\right]_0^4$

$\displaystyle A = \left[4(4)^2 - \frac{2}{3} (4)^3+C \right] - \left[4(0)^2 - \frac{2}{3} (0)^3 + C\right] = \left(64 - \frac{128}{3} \right)-(0)$

$\displaystyle A = \frac{64}{3}$

Calculando el momento $M_x$

$\displaystyle M_x = \frac{1}{2} \int_a^b{ \left\{[f(x)]^2-[g(x)]^2 \right\} dx}$

Pero como $g(x) \ge f(x)$

$\displaystyle M_x = \frac{1}{2} \int_a^b{ \left\{[g(x)]^2-[f(x)]^2\right\} \, dx}$

Continuando

$\displaystyle M_x = \frac{1}{2} \int_0^4{ [(6x-x^2-3)^2-(x^2-2x-3)^2 ] \, dx}$

$\displaystyle M_x = \frac{1}{2} \int_0^4{[(36x^2+x^4+9-12x^3-36x+6x^2 )-(x^4+4x^2+9-4x^3-6x^2+12x)] \, dx}$

$\displaystyle M_x = \frac{1}{2} \int_0^4{[(x^4-12x^3+42x^2-36x)-(x^4-4x^3-2x^2+12x)] \, dx}$

$\displaystyle M_x = \frac{1}{2} \int_0^4{(x^4-12x^3+42x^2-36x-x^4+4x^3+2x^2-12x) \, dx}$

$\displaystyle M_x = \frac{1}{2} \int_0^4{(-8x^3+44x^2-48x) \, dx} = \frac{1}{2} \left[-2x^4 + \frac{44}{3} x^3-24x^2 \right]_0^4$

$\displaystyle M_x = \frac{1}{2} \left\{\left[-2(4)^4 + \frac{44}{3} (4)^3-24(4)^2 \right] - \left[-2(0)^4+\frac{44}{3} (0)^3-24(0)^2 \right] \right\}$

$\displaystyle M_x = \frac{1}{2} \left\{\left[-2(256) + \frac{44}{3} (64)-24(16)\right] - (0) \right\}$

$\displaystyle M_x = \frac{1}{2} \left(-512+\frac{2816}{3}-384 \right) = \frac{1}{2} \left(\frac{128}{3} \right)$

$\displaystyle M_x = \frac{64}{3}$

Calculando el momento $M_y$

$\displaystyle M_y = \int_a^b{x[f(x)-g(x)] \, dx}$

Pero como $g(x) \ge f(x)$

$\displaystyle M_y = \int_a^b{x[g(x)-f(x)] \, dx}$

Continuando

$\displaystyle M_y = \int_0^4{x[(6x-x^2-3)-(x^2-2x-3)] \, dx}$

$\displaystyle M_y = \int_0^4{x(6x-x^2-3-x^2+2x+3) \, dx} = \int_0^4{x(8x-2x^2 ) \, dx}$

$\displaystyle M_y = \int_0^4{(8x^2-2x^3 ) \, dx} = \left[\frac{8}{3} x^3-\frac{1}{2} x^4 \right]_0^4$

$\displaystyle M_y = \left[\frac{8}{3} (4)^3-\frac{1}{2} (4)^4 \right]-\left[\frac{8}{3} (0)^3-\frac{1}{2} (0)^4 \right] = (\frac{512}{3}-\frac{256}{2})-(0) = \frac{128}{3}$

$\displaystyle M_y = \frac{128}{3}$

Calculando las coordenadas del centro de gravedad

\displaystyle \overline{x} = \frac{\frac{128}{3}}{\frac{64}{3}}

Finalmente, el centro de gravedad de la región sombreada es

$\therefore (\overline{x} , \overline{y}) = (2,1)$

Problema 2. Hallar el centro de gravedad del área en el primer cuadrante de la hipocicloide $x=a \cos^3{\theta}$ y $y =a \sin^3{\theta}$ .

Solución. Considerando que $a=1$ , se grafican las ecuaciones paramétricas

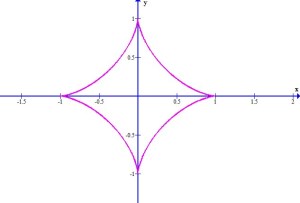
Analizando sólo el primer cuadrante

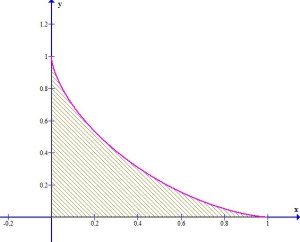
Ahora, sólo basta investigar los límites inferior y superior. Para ello, se utilizará la siguiente identidad

$x^2+y^2=1$

Sustituyendo (aun tomando en cuenta que $a=1$ )

$\displaystyle (\cos^3{\theta} )^2+(\sin^3{\theta})^2=1$

$\displaystyle (\cos^3{\theta} )^2+(\sin^2{\theta})^3=1$

$\displaystyle (\cos^3{\theta})^2 + (1-\cos^2{\theta} )^3=1$

$\displaystyle (\cos^6{\theta})+(1-3 \cos^2{\theta}+3 \cos^4{\theta}-\cos^6{\theta} )=1$

$\displaystyle 3 \cos^4{\theta} - 3 \cos^2{\theta} + 1 = 1$

$\displaystyle 3 \cos^4{\theta} - 3 \cos^2{\theta} = 0$

$\displaystyle 3 \cos^4{\theta} = 3 \cos^2{\theta}$

$\displaystyle \cos^2{\theta} = 1$

$\displaystyle \cos{\theta} = 1$

$\displaystyle \theta = \arccos{(1)} = 0$

Se tomará la fórmula

$\displaystyle A = \int_c^d{x \, dy}$

Los límites inferior y superior son $c=0$ y $\displaystyle d=\frac{\pi}{2}$ . Antes de aplicar la fórmula, se determinará lo siguiente

$y=a \sin^3{\theta}$

$\displaystyle \frac{dy}{d\theta} = 3a \sin^2{\theta} \cos{\theta}$

$\displaystyle dy = 3a \sin^2{\theta} \cos{\theta} \, d\theta$

Sustituyendo

$\displaystyle A = \int_c^d{x \, dy} = \int_0^{\frac{\pi}{2}}{(a \cos^3{\theta} )(3a \sin^2{ \theta} \cos{\theta}) \, d\theta}$

$\displaystyle A = 3a^2 \int_0^{\frac{\pi}{2}}{\cos^4{\theta} \sin^2{\theta} \, d\theta} = 3a^2 \int_0^{\frac{\pi}{2}}{(\cos^2{\theta})^2 \sin^2{\theta} \, d\theta}$

$\displaystyle A = 3a^2 \int_0^{\frac{\pi}{2}}{\left(\frac{1}{2}+ \frac{1}{2} \cos{2\theta} \right)^2 \left(\frac{1}{2} - \frac{1}{2} \cos{2\theta} \right) \, d\theta}$

$\displaystyle A = 3a^2 \int_0^{\frac{\pi}{2}}{\left(\frac{1}{4} + \frac{1}{2} \cos{2\theta} + \frac{1}{4} \cos^2{2\theta} \right) \left(\frac{1}{2}-\frac{1}{2} \cos{2\theta} \right) \, d\theta}$

$\displaystyle A = 3a^2 \int_0^{\frac{\pi}{2}}{\left[\frac{1}{4}+\frac{1}{2} \cos{2\theta} + \frac{1}{4} \left(\frac{1}{2} + \frac{1}{2} \cos{4\theta} \right) \right] \left(\frac{1}{2} - \frac{1}{2} \cos{2\theta} \right) \, d\theta}$

$\displaystyle A = 3a^2 \int_0^{\frac{\pi}{2}}{\left(\frac{1}{4} + \frac{1}{2} \cos{2\theta} + \frac{1}{8} + \frac{1}{8} \cos{4\theta} \right) \left(\frac{1}{2} - \frac{1}{2} \cos{2\theta} \right) \, d\theta}$

$\displaystyle A = 3a^2 \int_0^{\frac{\pi}{2}}{\left(\frac{3}{8} + \frac{1}{2} \cos{2\theta} + \frac{1}{8} \cos{4\theta} \right) \left(\frac{1}{2} - \frac{1}{2} \cos{2\theta} \right) \, d\theta}$

$\displaystyle A = 3a^2 \int_0^{\frac{\pi}{2}}{\left(\frac{3}{16} - \frac{3}{16} \cos{2\theta} + \frac{1}{4} \cos{2\theta} - \frac{1}{4} \cos^2{2\theta} + \frac{1}{16} \cos{4\theta} - \frac{1}{16} \cos{4\theta} \cos{2\theta} \right) \, d\theta}$

$\displaystyle A = 3a^2 \int_0^{\frac{\pi}{2}}{\left[\frac{3}{16} + \frac{1}{16} \cos{2\theta} - \frac{1}{4} \left(\frac{1}{2} + \frac{1}{2} \cos{4\theta} \right) + \frac{1}{16} \cos{4\theta} - \frac{1}{16} \cos{4\theta} \cos{2\theta} \right] \, d\theta}$

$\displaystyle A = 3a^2 \int_0^{\frac{\pi}{2}}{\left(\frac{3}{16} + \frac{1}{16} \cos{2\theta} - \frac{1}{8} - \frac{1}{8} \cos{4\theta} + \frac{1}{16} \cos{4\theta} - \frac{1}{16} \cos{4\theta} \cos{2\theta} \right) \, d\theta}$

$\displaystyle A = 3a^2 \int_0^{\frac{\pi}{2}}{\left(\frac{1}{16} + \frac{1}{16} \cos{2\theta} - \frac{1}{16} \cos{4\theta} - \frac{1}{16} \cos{4\theta} \cos{2\theta} \right) \, d\theta}$

$\displaystyle A = 3a^2 \left[\frac{1}{16} \int_0^{\frac{\pi}{2}}{d\theta} + \frac{1}{16} \int_0^{\frac{\pi}{2}}{\cos{2\theta} \ d\theta} - \frac{1}{16} \int_0^{\frac{\pi}{2}}{\cos{4\theta} \ d\theta} - \frac{1}{16} \int_0^{\frac{\pi}{2}}{\cos{4\theta} \cos{2\theta} \ d\theta} \right]$

$\displaystyle A = 3a^2 \left[\frac{1}{16} \theta + \frac{1}{32} \sin{2\theta} - \frac{1}{64} \sin{4\theta} - \frac{1}{16} \left[ \frac{1}{2(4+2)} \sin{(4+2)\theta} + \frac{1}{2(4-2)} \sin{(4-2)\theta} \right] \right]_0^{\frac{\pi}{2}}$

$\displaystyle A = 3a^2 \left[\frac{1}{16} \theta + \frac{1}{32} \sin{2\theta} - \frac{1}{64} \sin{4\theta} - \frac{1}{192} \sin{6\theta} - \frac{1}{64} \sin{2\theta} \right]_0^{\frac{\pi}{2}}$

$\displaystyle \begin{matrix} A & = & 3a^2 \left\{\left[\frac{1}{16} (\frac{\pi}{2}) + \frac{1}{32} \sin{2(\frac{\pi}{2})} - \frac{1}{64} \sin{4(\frac{\pi}{2})} - \frac{1}{192} \sin{6(\frac{\pi}{2})} - \frac{1}{64} \sin{2(\frac{\pi}{2})} \right] \right. \\ \\ & &- \left. \left[\frac{1}{16} (0) + \frac{1}{32} \sin{2(0)} - \frac{1}{64} \sin{4(0)} - \frac{1}{192} \sin{6(0)} - \frac{1}{64} \sin{2(0)} \right] \right\} \end{matrix}$

$\displaystyle A = 3a^2 \left\{ \left[\frac{\pi}{32} + \frac{1}{32} \sin{\pi} - \frac{1}{64} \sin{2\pi} - \frac{1}{192} \sin{3\pi} - \frac{1}{64} \sin{\pi} \right] - \left[(0) + \frac{1}{32} \sin{0} - \frac{1}{64} \sin{0} - \frac{1}{192} \sin{0} - \frac{1}{64} \sin{0} \right] \right\}$

$\displaystyle A = 3a^2 (\frac{\pi}{32}) - 3a^2 (0) = \frac{3\pi}{32} a^2$

$\displaystyle A = \frac{3\pi}{32} a^2$

Calculando el momento $M_x$

$\displaystyle M_x = \int_c^d{xy \, dy} = \int_0^{\frac{\pi}{2}}{(a \cos^3{\theta})(a \sin^3{\theta})(3a \sin^2{\theta} \cos{\theta}) \, d\theta}$

$\displaystyle M_x = 3a^3 \int_0^{\frac{\pi}{2}}{\sin^5{\theta} \cos^4{\theta} \, d\theta} = 3a^3 \int_0^{\frac{\pi}{2}}{\sin^5{\theta} \cos^4{\theta} \, d\theta}$

$\displaystyle M_x = 3a^3 \int_0^{\frac{\pi}{2}}{\sin^4{\theta} \sin{\theta} \cos^4{\theta} \, d\theta} = 3a^3 \int_0^{\frac{\pi}{2}}{(1-\cos^2{\theta} )^2 \sin{\theta} \cos^4{\theta} \, d\theta}$

$\displaystyle M_x = 3a^3 \int_0^{\frac{\pi}{2}}{(1 - 2 \cos^2{\theta} + \cos^4{\theta}) \sin{\theta} \cos^4{\theta} \, d\theta}$

$\displaystyle M_x = 3a^3 \int_0^{\frac{\pi}{2}}{(\cos^4{\theta} - 2 \cos^6{\theta} + \cos^8{\theta}) \sin{\theta} \, d\theta}$

$\displaystyle M_x = 3a^3 \left[\int_0^{\frac{\pi}{2}}{\cos^4{\theta} \sin{\theta} \ d\theta} - 2 \int_0^{\frac{\pi}{2}}{\cos^6{\theta} \sin{\theta} \ d\theta} + \int_0^{\frac{\pi}{2}}{\cos^8{\theta} \sin{\theta} \, d\theta} \right]$

$\displaystyle M_x = 3a^3 \left[-\frac{1}{5} \cos^5{\theta} + \frac{2}{7} \cos^7{\theta} - \frac{1}{9} \cos^9{\theta} + C \right]_0^{\frac{\pi}{2}}$

$\displaystyle M_x = 3a^3 \left[\left(-\frac{1}{5} \cos^5{\frac{\pi}{2}} + \frac{2}{7} \cos^7{\frac{\pi}{2}} - \frac{1}{9} \cos^9{\frac{\pi}{2}} \right) - \left(-\frac{1}{5} \cos^5{0} + \frac{2}{7} \cos^7{0} - \frac{1}{9} \cos^9{0} \right) \right]$

$\displaystyle M_x = 3a^3 \left\{\left[-\frac{1}{5} (0) + \frac{2}{7} (0) - \frac{1}{9} (0) \right] - \left[-\frac{1}{5} (1) + \frac{2}{7} (1) - \frac{1}{9} (1)\right] \right\}$

$\displaystyle M_x = -3a^3 \left(-\frac{1}{5} + \frac{2}{7} - \frac{1}{9} \right) = -3a^3 \left(-\frac{8}{315} \right) = \frac{24}{315} a^3$

$\displaystyle M_x = \frac{24}{315} a^3$

Calculando el momento $M_y$

$\displaystyle M_y = \frac{1}{2} \int_c^d{x^2 \, dy} = \frac{1}{2} \int_0^{\frac{\pi}{2}}{(a \cos^3{\theta})^2 (3a \sin^2{\theta} \cos{\theta} \, d\theta})$

$\displaystyle M_y = \frac{3}{2} a^3 \int_0^{\frac{\pi}{2}}{\cos^6{\theta} \sin^2{\theta} \, d\theta} = \frac{3}{2} a^3 \int_0^{\frac{\pi}{2}}{(\cos^2{\theta})^3 \sin^2{\theta} \, d\theta}$

$\displaystyle M_y = \frac{3}{2} a^3 \int_0^{\frac{\pi}{2}}{(1 - \sin^2{\theta})^3 \cos{\theta} \sin^2{\theta} \, d\theta}$

$\displaystyle M_y = \frac{3}{2} a^3 \int_0^{\frac{\pi}{2}}{(1 - 3\sin^2{\theta} + 3 \sin^4{\theta} - \sin^6{\theta}) \cos{\theta} \sin^2{\theta} \, d\theta}$

$\displaystyle M_y = \frac{3}{2} a^3 \int_0^{\frac{\pi}{2}}{(\sin^2{\theta} - 3 \sin^4{\theta} + 3 \sin^6{\theta} - \sin^8{\theta}) \cos{\theta} \, d\theta}$

$\displaystyle M_y = \frac{3}{2} a^3 \left[\frac{1}{3} \sin^3{\theta} - \frac{3}{5} \sin^5{\theta} + \frac{3}{7} \sin^7{\theta} - \frac{1}{9} \sin^9{\theta} + C \right]_0^{\frac{\pi}{2}}$

$\displaystyle M_y = \frac{3}{2} a^3 \left[ \frac{1}{3} \sin^3{\frac{\pi}{2}} - \frac{3}{5} \sin^5{\frac{\pi}{2}} + \frac{3}{7} \sin^7{\frac{\pi}{2}} - \frac{1}{9} \sin^9{\frac{\pi}{2}} \right] - \frac{3}{2} a^3 \left[\frac{1}{3} \sin^3{0} - \frac{3}{5} \sin^5{0} + \frac{3}{7} \sin^7{0} - \frac{1}{9} \sin^9{0} \right]$

$\displaystyle M_y = \frac{3}{2} a^3 \left[ \left(\frac{1}{3} \sin^3{\frac{\pi}{2}} - \frac{3}{5} \sin^5{\frac{\pi}{2}} + \frac{3}{7} \sin^7{\frac{\pi}{2}} - \frac{1}{9} \sin^9{\frac{\pi}{2}} \right) - \left(\frac{1}{3} \sin^3{0} - \frac{3}{5} \sin^5{0} + \frac{3}{7} \sin^7{0} - \frac{1}{9} \sin^9{0} \right) \right]$

$\displaystyle M_y = \frac{3}{2} a^3 \left[ \left(\frac{1}{3} - \frac{3}{5} + \frac{3}{7} - \frac{1}{9} \right) - (0) \right] = \frac{3}{2} a^2 \left(\frac{16}{315} \right)$