Volúmenes de sección transversal. Cálculo integral.

Introducción

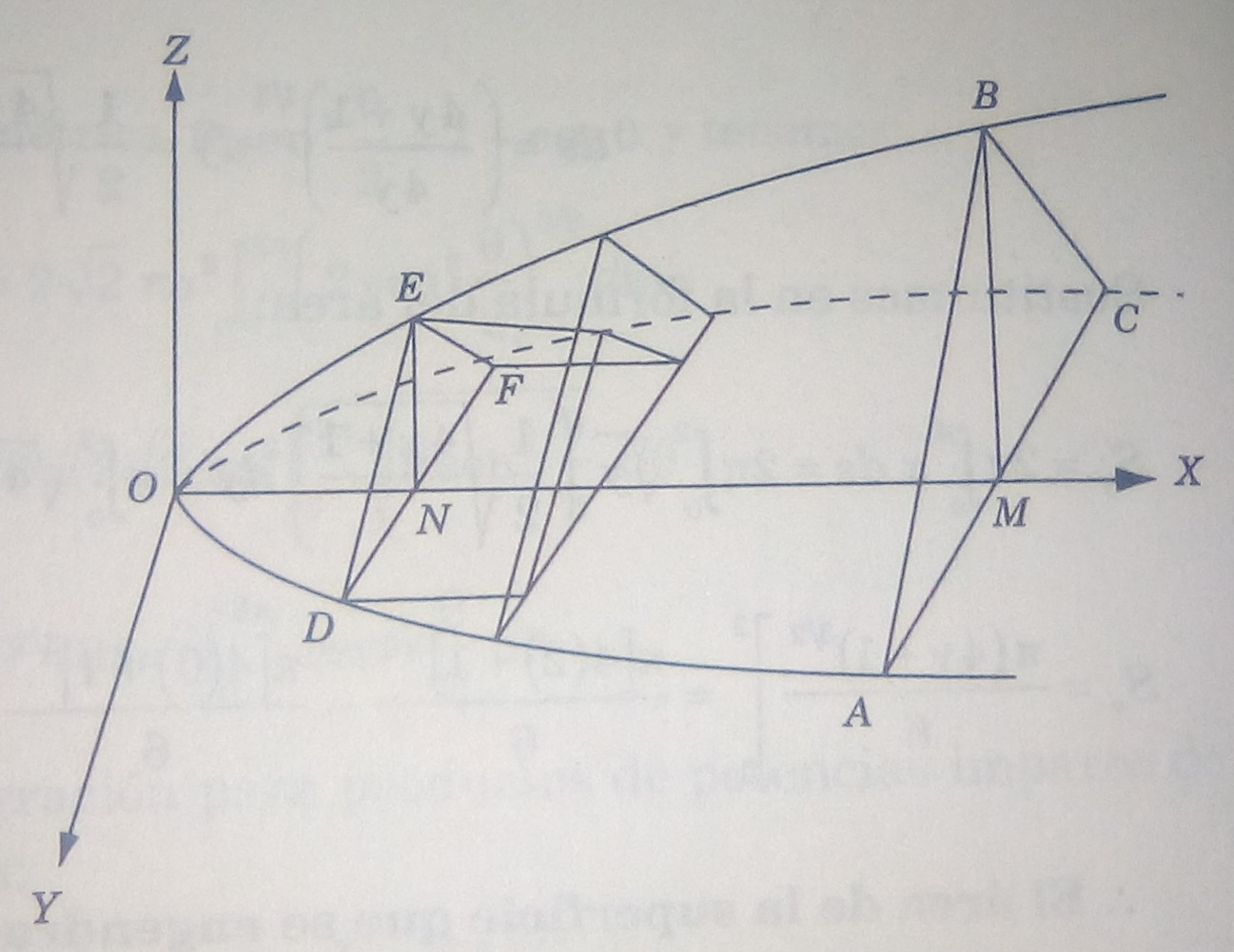
Considerando la figura 1, todas las secciones transversales por planos perpendiculares al eje X son círculos. Si $OM=x$ y $MB=y$ , entonces el área de la sección transversal $ABCD = \pi y^2 = \pi [\phi (x)]^2$ , si $y=\phi (x)$ es la ecuación de la curva engendradora $OBF$ . Por tanto, el área de la sección transversal por cualquier plano perpendicular a $OX$ es u función de su distancia $(=x)$ al punto $O$ .

Siempre que sea posible expresar el área de una sección cualquier del sólido, que sea perpendicular a una recta fija (como el eje $X$ ). Se hará como una función de su distancia a un punto fijo (como el origen $O$ ).

Se divide el sólido en $n$ rebanadas, cada una de espesor $\Delta x$ , por secciones equidistantes perpendiculares al eje $X$ . Sea $EDF$ una cara de una de las rebanadas y sea $ON=x$ (figura 2), por hipótesis

$\displaystyle \text{Area} (EDF) = A(x)$

El volumen de esta rebanada es igual, aproximadamente, a:

$\displaystyle \text{Area} (EDF) \cdot \Delta x = A(x) \Delta x (\text{base} \times \text{altura})$

Entonces $\displaystyle \sum_{i=1}^n{A(x_i ) \Delta x_i}$ representa la suma de los volúmenes de todos esos prismas.

Es cierto que el volumen pedido es el límite de esta suma; por tanto, y de acuerdo con el teorema fundamental del cálculo integral, se tiene que

$\displaystyle V = \lim_{n \rightarrow \infty}{\sum_{i=1}^n{A(x_i ) \Delta x_i} } = \int_{\alpha}^{\beta}{A(x) \, dx}$

Por tanto, resulta

$\displaystyle V = \int_{\alpha}^{\beta}{A(x) \, dx}$

El elemento de volumen es un prisma (otras veces es un cilindro) cuya altura es $dx$ y cuya base tiene como área $A(x)$ . Es decir, $dv=A(x) \, dx$ .

Si las secciones son perpendiculares al eje $Y$ , el volumen viene dado por

$\displaystyle V = \int_{\gamma}^{\eta}{A(y) \, dy}$

Donde $A(y)$ es el área de la sección en $y$ .

Problemas resueltos

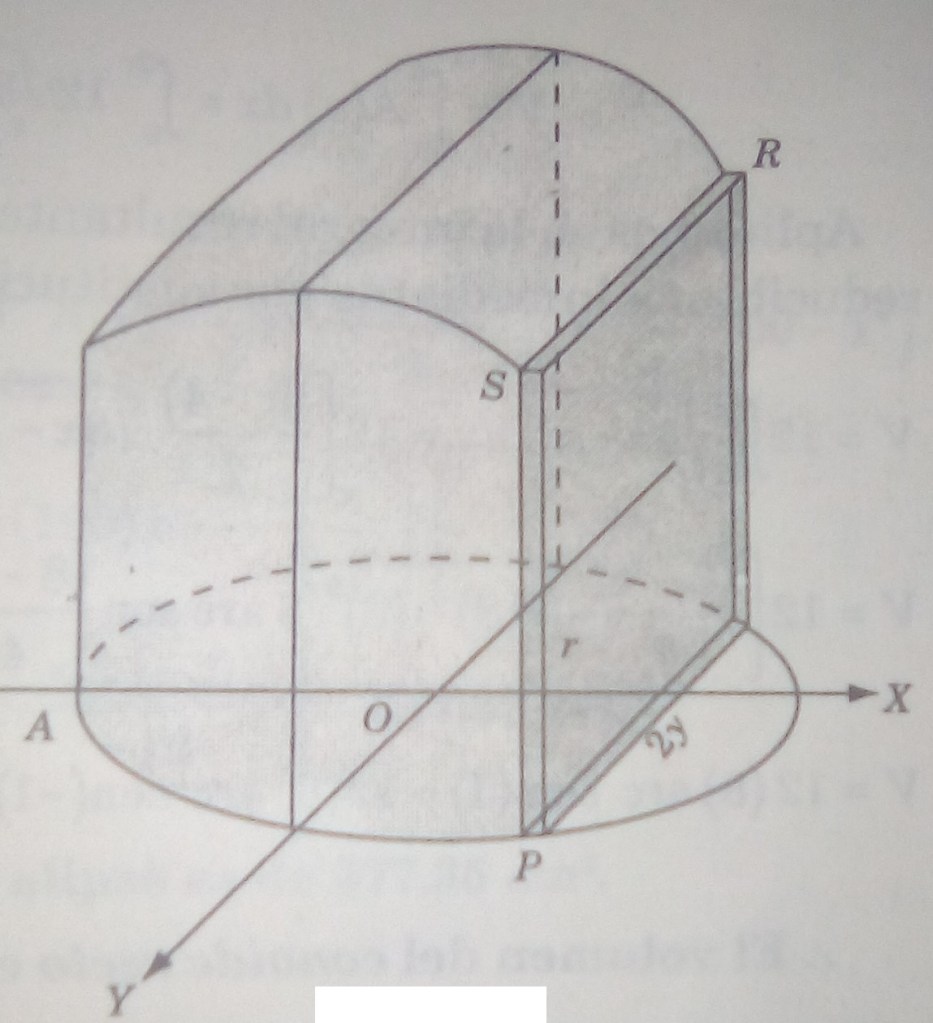
Problema 1. La base de un sólido es un círculo de 5 cm de radio. Todas las secciones perpendiculares a un diámetro fijo de la base son cuadrados. Calcular el volumen del sólido.

Solución. Siendo la base del círculo $x^2+y^2=5^2=25$ en el plano $XY$ y $OX$ el diámetro fijo (figura 3). Con base en el enunciado la sección $PSRQ$ perpendicular a $OX$ es un cuadrado, cuya área es $4y^2$ , si $PQ=2y$ . De la ecuación $x^2+y^2=25$ , se tiene que $y^2=25-x^2$ ; el área de la sección $PSRQ$ que se representa como $A(x)$ es igual a $4y^2$ , es decir, $4(25-x^2 )$ .

Aplicando la fórmula de volumen

$\displaystyle V = \int_{\alpha}^{\beta}{A(x) \, dx} = \int_{-5}^5{4(25-x^2 ) \, dx}$

$\displaystyle V = 4 \left[ 25x - \frac{1}{3} x^3+C \right]_{-5}^5$

$\displaystyle V = 4 \left[ 25(5) - \frac{1}{3} (5)^3 + C\right] - 4 \left[ 25(-5) - \frac{1}{3} {(-5)}^3+C \right]$

$\displaystyle = 4 \left[ \left(125-\frac{125}{3} \right) - \left(-125+\frac{125}{3} \right) \right] = \frac{2000}{3}$

Finalmente

$\displaystyle \therefore V =\frac{2000}{3} \, \text{(cm)}^3$

Problema 2. Calcular el volumen de un conoide recto de 12 cm de altura ( $h$ ), cuya base es el círculo $x^2+y^2=8x$ de 4 cm de radio ( $r$ ).

Solución. En base a la figura 4, se considera la sección $PQR$ es perpendicular al eje $OX$ ; dicha sección es un triángulo isósceles, donde $RM=y$ , es decir:

$\displaystyle RM = \sqrt{8x-x^2}$

Dicho valor se obtiene de la ecuación $x^2+y^2=8x$ que representa la circunferencia $ORAQ$ .

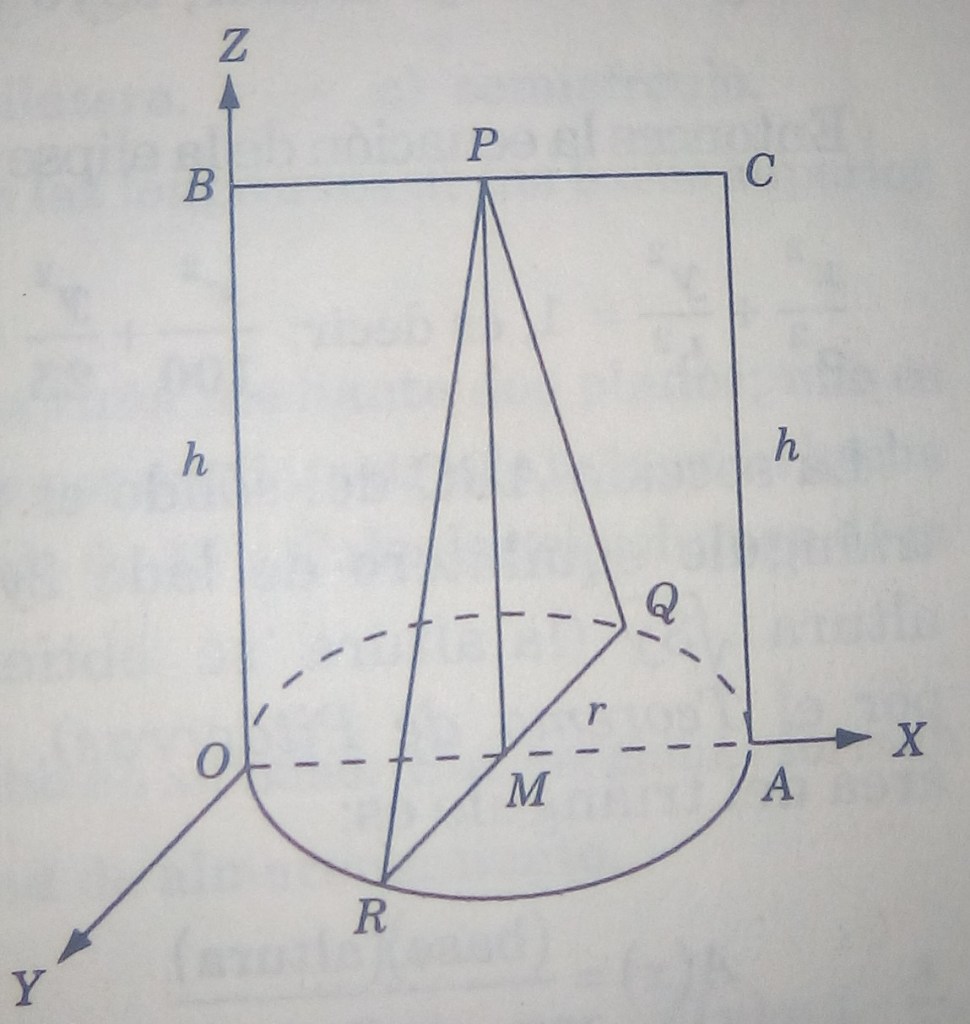
En la sección $PQR$ se observa que la base

$\displaystyle RQ = 2y = 2\sqrt{8x-x^2}$

Y la altura

$\displaystyle MP = h = 12 \ \text{cm}$

Entonces el área de dicha sección es

$\displaystyle A(x) = \frac{\text{base} \times \text{altura}}{2} = \frac{(2\sqrt{8x-x^2})(12)}{2}$

$\displaystyle A(x) = 12\sqrt{8x-x^2}$

Aplicando la fórmula de volumen

$\displaystyle V = \int_{\alpha}^{\beta}{A(x) \, dx}$

$\displaystyle V = \int_0^{2r}{12 \sqrt{8x-x^2} \, dx} = \int_0^8{12\sqrt{8x-x^2} \, dx}$

$\displaystyle V = 12 \int_0^8{\sqrt{8x-x^2} \, dx}$

Resolviendo la integral definida como una indefinida

$\displaystyle \int_0^8{\sqrt{8x-x^2} \, dx} \quad \rightarrow \quad \int{\sqrt{8x-x^2} \, dx}$

Aplicando el método de integración por sustitución algebraica, resulta

$\displaystyle \int{\sqrt{8x-x^2} \, dx} = \int{\sqrt{-(x^2-8x)} \, dx} = \int{\sqrt{-(x^2-8x+16-16)} \, dx}$

$\displaystyle \int{\sqrt{8x-x^2} \, dx} = \int{\sqrt{16-(x^2-8x+16)} \, dx} = \int{\sqrt{16-(x-4)^2} \, dx}$

$\displaystyle \int{\sqrt{8x-x^2} \, dx} = \left(\frac{x-4}{2} \right) \sqrt{16-(x-4)^2} + \frac{16}{2} \arcsin{\left(\frac{x-4}{4} \right)} + C$

$\displaystyle \int{\sqrt{8x-x^2} \, dx} = \left(\frac{x-4}{2} \right) \sqrt{16-(x-4)^2} + 8 \arcsin{\left(\frac{x-4}{4} \right)} + C$

Regresando, sustituyendo y reemplazando la variable $x$ por sus límites correspondientes

$\displaystyle \int_0^8{12 \sqrt{8x-x^2} \, dx} = \left[\left(\frac{x-4}{2} \right) \sqrt{16-(x-4)^2} + 8 \arcsin{\left(\frac{x-4}{4} \right)} + C \right]_0^8$

$\displaystyle = \left[ \left(\frac{4}{2} \right) \sqrt{16-(4)^2} + 8 \arcsin{\left(\frac{4}{4} \right)} \right] - 12 \left[ \left(\frac{-4}{2} \right) \sqrt{16-(-4)^2} + 8 \arcsin{\left(\frac{-4}{4} \right)} \right]$

$\displaystyle = \left[ 2\sqrt{16-16} + 8 \arcsin{(1)} \right] - \left[-2\sqrt{16-16} + 8 \arcsin{(-1)} \right]$

$\displaystyle \int_0^8{\sqrt{8x-x^2} \, dx} = 4\pi - (-4\pi) = 8 \pi$

Finalmente

$\displaystyle V = 12 \int_0^8{\sqrt{8x-x^2} \, dx}$

$\displaystyle V = 12 (8\pi)$

$\displaystyle \therefore V = 96\pi \ \text{cm}^3$

Nota: se debe comprobar que el volumen del conoide debe ser la mitad del volumen del cilindro de las mismas base y altura.

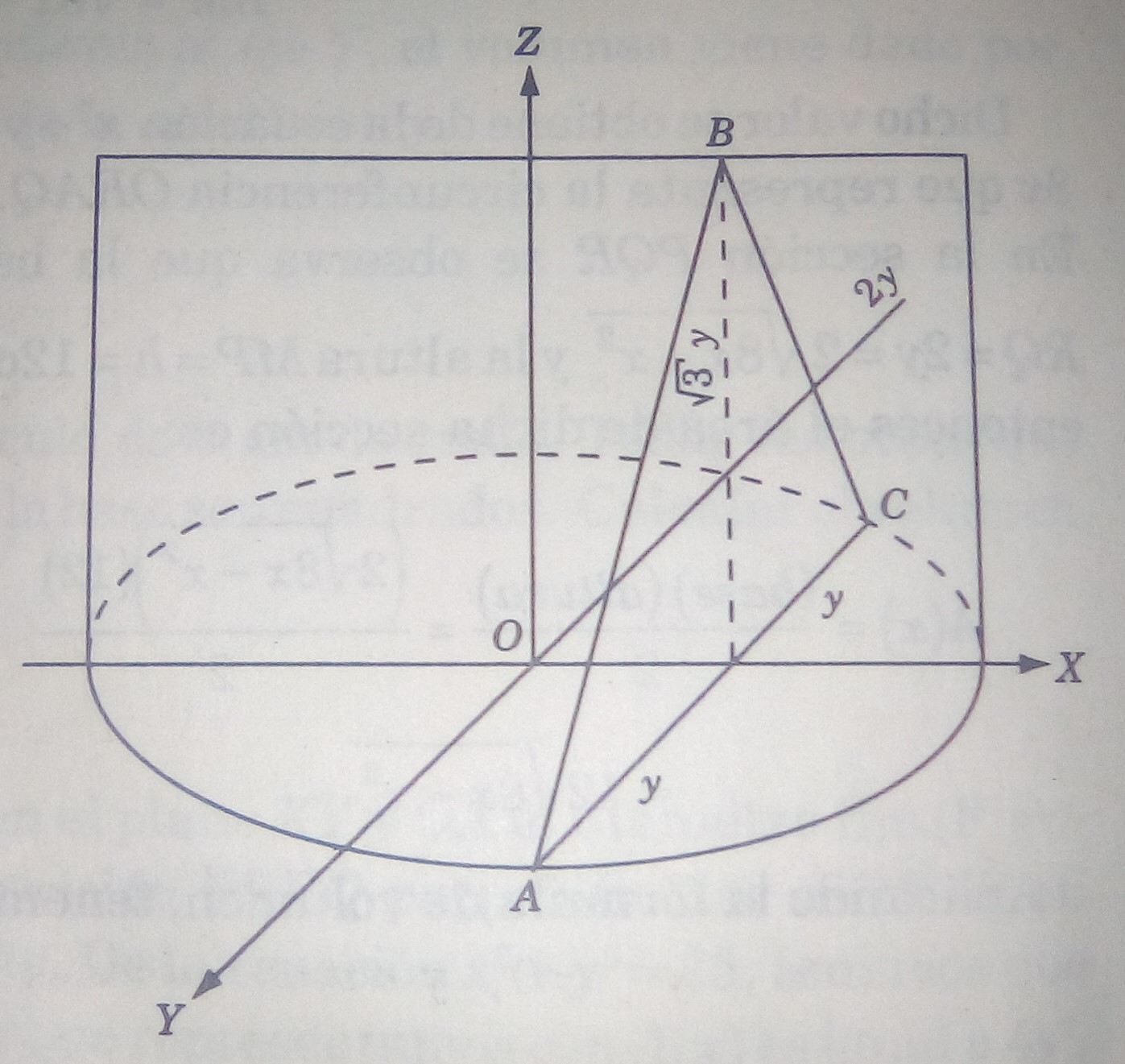
Problema 3. La base de un sólido tiene la forma de una elipse con el eje mayor de 20 cm y eje menor de 10 cm. Calcular el volumen del sólido si cada sección perpendicular al eje mayor es un triángulo equilátero.

Solución. En la figura 5, se observa la elipse y todo lo mencionado del problema; sea $2a$ la longitud del eje mayor, cuyo valor es de 20 cm, por lo que se deduce que $a=10$ ; de igual manera, sea $2b$ la longitud del eje menor, cuyo valor es de 10 cm, por lo que $b=5$ .

La ecuación de la elipse es

$\displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} =1$

Es decir

$\displaystyle \frac{x^2}{10^2} + \frac{y^2}{5^2} = 1$

$\displaystyle \frac{x^2}{100} + \frac{y^2}{25} = 1$

Despejando $y$

$\displaystyle \frac{y^2}{25} = 1 - \frac{x^2}{100}$

$\displaystyle y^2 = 25(1 - \frac{x^2}{100}) = \frac{25}{100} (100-x^2 )$

$\displaystyle y = \pm \sqrt{\frac{25}{100} (100-x^2 )} = \frac{5}{10} \sqrt{100-x^2} = \frac{1}{2} \sqrt{100-x^2}$

La sección $ABC$ del sólido es un triángulo equilátero de lado $2y$ y altura $\sqrt{3} y$ (la altura se obtuvo por el teorema de Pitágoras). El área del triángulo es

$\displaystyle A(x) = \frac{\text{base} \times \text{altura}}{2}$

$\displaystyle A(x) = \frac{2y \times \sqrt{3} y}{2} = \sqrt{3} y^2$

Por tanto, el área de la sección $ABC$ es

$\displaystyle A(x) = \sqrt{3} (\frac{1}{2} \sqrt{100-x^2})^2 = \sqrt{3} (\frac{1}{4})(100 - x^2) = \frac{\sqrt{3}}{4} (100-x^2 )$

Aplicando la fórmula del volumen

$\displaystyle V = \int_{\alpha}^{\beta}{A(x) \, dx} = \int_{-10}^{10}{\frac{\sqrt{3}}{4} (100-x^2) \, dx} = \frac{\sqrt{3}}{4} \int_{-10}^{10}{(100-x^2) \, dx}$

$\displaystyle = \frac{\sqrt{3}}{4} \left[100x-\frac{1}{3} x^3+C\right]_{-10}^10 = \frac{\sqrt{3}}{4} \left[100(10)-\frac{1}{3} (10)^3+C\right] - \frac{\sqrt{3}}{4} \left[100(-10)-\frac{1}{3} {(-10)}^3+C \right]$

$\displaystyle = \frac{\sqrt{3}}{4} \left[1000-\frac{1}{3} (1000)\right]-\frac{\sqrt{3}}{4} \left[-1000+\frac{1}{3} (1000)\right]$

$\displaystyle = \frac{\sqrt{3}}{4} \left[1000-\frac{1000}{3}\right] - \frac{\sqrt{3}}{4} \left[-1000+\frac{1000}{3}\right] = \frac{\sqrt{3}}{4} (\frac{2000}{3}) - \frac{\sqrt{3}}{4} (-\frac{2000}{3})$