Introducción
Al emplear el teorema de Thévenin es posible determinar la potencia máxima que puede suministrar un circuito y cómo asjutar la carga para efectuar la transferencia máxima.
Suponga que se tiene el circuito de la figura 1. La expresión siguiente indica la potencia de esta expresión que se entrega a la carga:
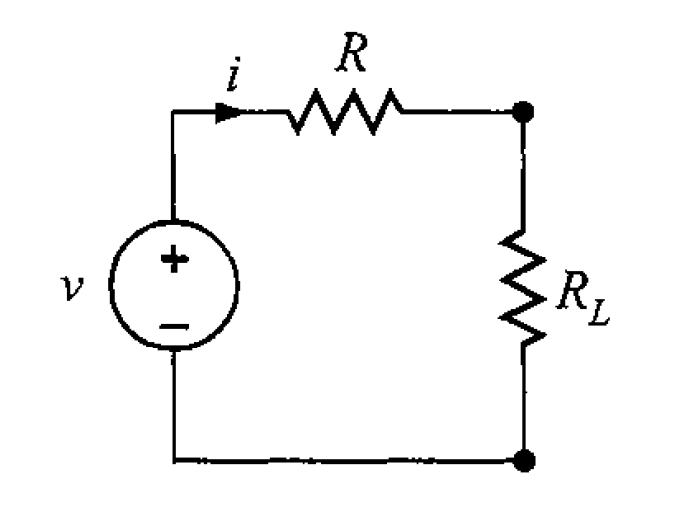
Se desea determinar el valor de que maximiza esta cantidad. Para ello, se deriva lo anterior con respecto a
y luego se iguala a cero.
Esto significa que la transferencia máxima de potencia se da cuando la resistencia de carga .
Problemas resueltos
Problema 1. Encuentre el valor de para la transferencia máxima de potencia en la red de la figura 2, así como la potencia máxima que puede entregarse a esta carga.

Solución. Primero, se obtiene el circuito equivalente de Thévenin de la red sin la carga (figura 3).
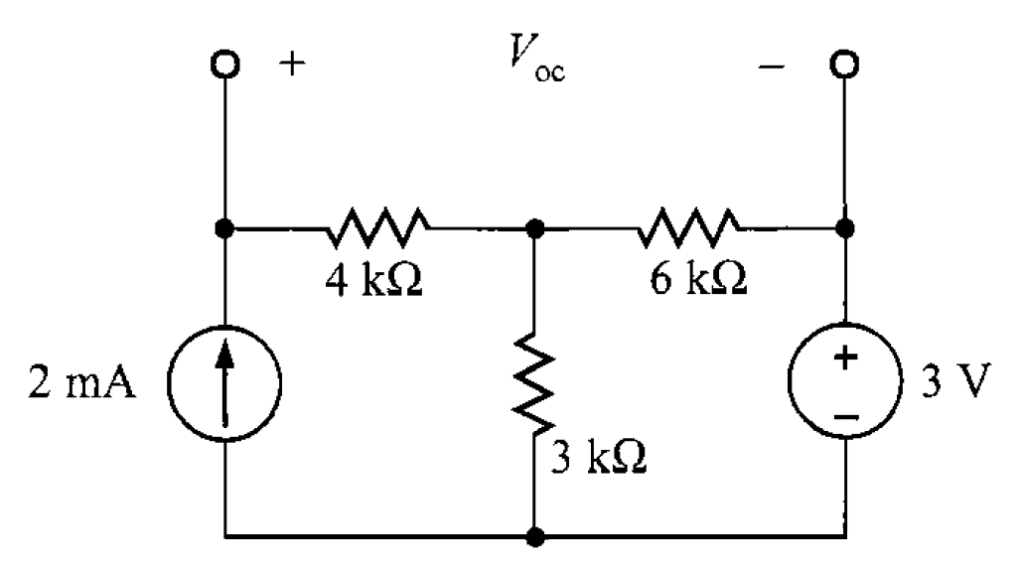

Después, el valor de se calcula obtiene los valores de
y
(figura 3). Para obtener los valores de corriente de malla se utiliza el análisis de mallas (figura 4). La ecuación de la primera malla es
Y la ecuación de la segunda malla, resulta
Resolviendo las ecuaciones, se sabe que es
Con estos datos, el valor de es
El siguiente paso es calcular la resistencia Thévenin haciendo que la fuente de corriente sea un circuito abierto y que la fuente de voltaje sea un cortocircuito (figura 5).
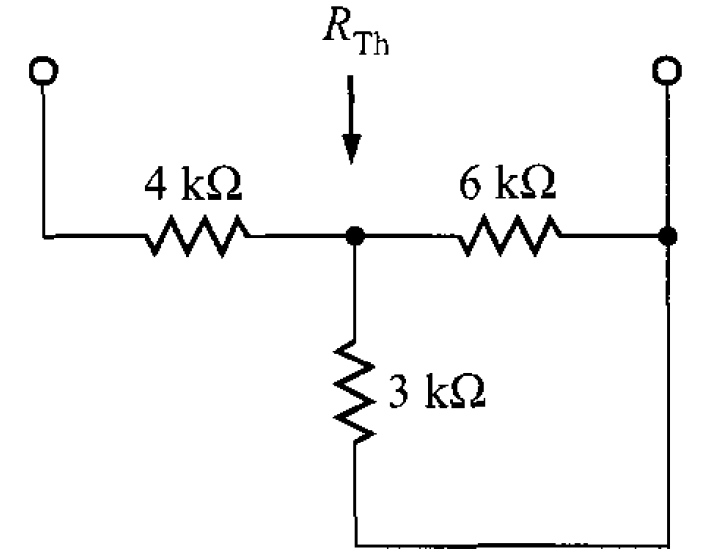
Por lo tanto, la transferencia máxima de potencia es
Y la potencia máxima que se entrega a la carga es
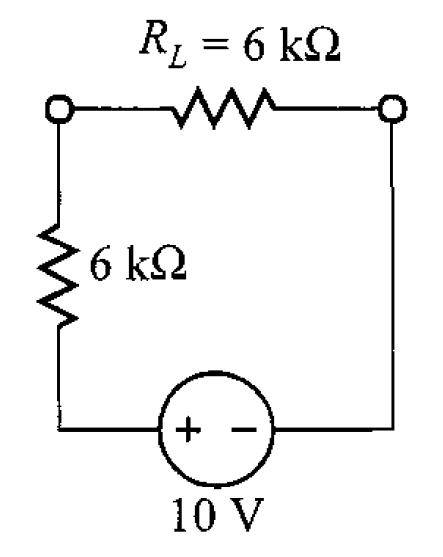
Problema 2. Encuentre el valor de para la transferencia máxima de potencia y la potencia máxima que puede entregarse a esta carga en el circuito de la figura 7.
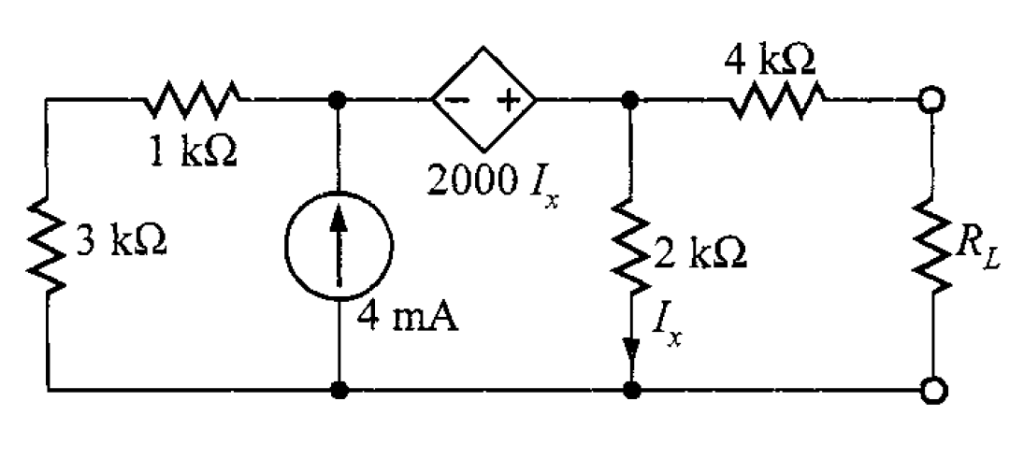
Solución. Se abre el circuito a la izquierda del resistor de 4 kΩ quedando de la siguiente manera (figura 8).
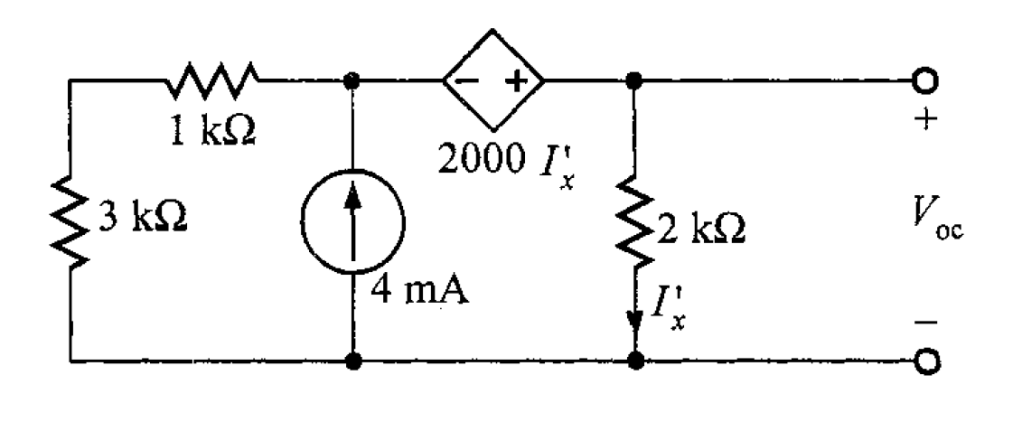
En la figura 8, se tiene un supernodo alrededor de la fuente dependiente y sus nodos de conexión. Aplicando la LKC en el supernodo resulta que
Y la ecuación de restricción es
Sustituyendo en la ecuación anterior
Ahora, se cortocircuitarán las terminales A-B como se observa que la figura 9.
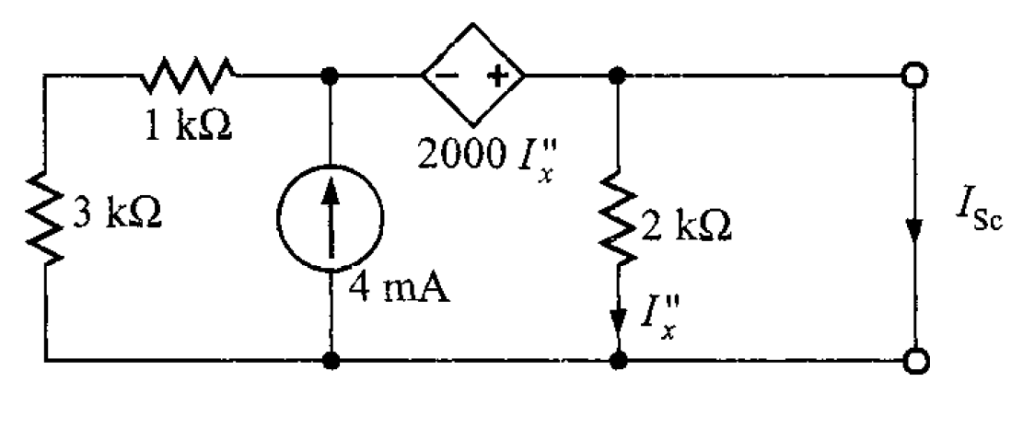
Esto provoca que el resistor de 2 kΩ sea un cortocircuito y que . En consecuencia la fuente dependiente será 0 V y la corriente
es de 4 mA. Este cambio se muestra en la figura 10.
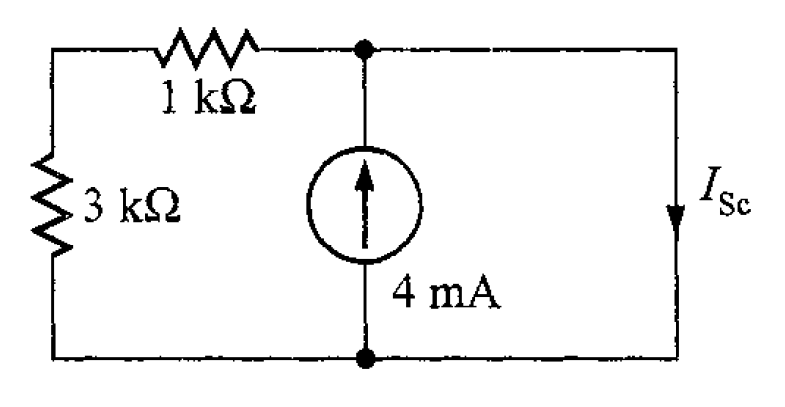
Con los valores de y
se obtiene la resistencia de Thévenin.
Conectando el equivalente de Thévenin al resto del circuito original se produce la red de la figura 11.

Entonces, la transferencia máxima de potencia es
Finalmente, la potencia máxima entregada es