Capacitores. Circuitos eléctricos.

Introducción

Un capacitor es un elemento de circuito que consiste en dos superficies conductoras separadas por un material no conductor o dieléctrico. La figura 1 muestra un capacitor y su símbolo eléctrico.

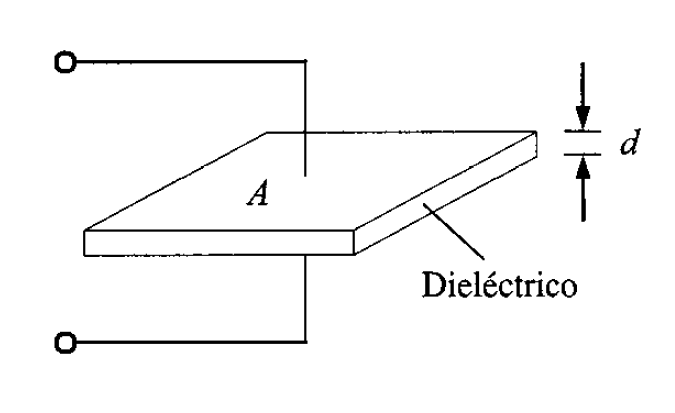
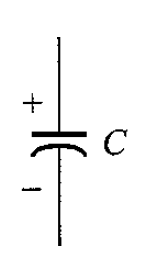
Figura 1. Representando el capacitor y su símbolo eléctrico.

Existen diferentes tipos de capacitores, y se clasifican por el tipo de material dieléctrico utilizando entre las placas conductoras. Aunque cualquier buen aislante puede servir como dieléctrico, cada tipo tiene características que lo hacen más adecuado para aplicaciones particulares.

Para aplicaciones particulares en circuitos eléctronicos (por ejemplo, el acoplamiento entre etapas de amplificación) el material dieléctrico puede ser papel impregnado de aceite o cera, mylar, poliestireno, mica, vidrio o cerámica.

Los capacitores con dieléctrico de cerámica construidos con titanatos de bario tienen una relación de capacitancia a volumen grande debido a su alta constante dieléctrica. Los capacitores con dieléctricos de mica, vidrio y cerámica operan satisfactoriamente a altas frecuencias.

Los capacitores electrolíticos de aluminio, que consisten en un par de placas de aluminio separadas por un electrolíto de pasta de bórax humedcida, proporcionan valores altos de capacitancia en volúmenes pequeños. Normalmente se usan en filtros, derivaciones y acoplamientos, fuentes de voltaje y aplicaciones para arranque de motores. Los capacitores electrolíticos de tantalio tienen pérdidas menores y características más estables que los capacitores electrolíticos de aluminio. La figura 2 muestra diversos capacitores discretos típicos.

Figura 2. Capacitores electrolíticos.

Además de estos capacitores, los cuales pueden insertarse deliberadamente en una red para aplicaciones específicas, la capacitancia parásita aparece siempre que existe una diferencia de potencial entre dos materiales semiconductores separados por un dieléctrico. Debe tenerse cuidado extremo en la distribución de sistemas electrónicos sobre tarjetas de circuito impreso, ya que esta capacitancia parásita puede producir acoplamientos indeseados entre circuitos.

La capacitancia se mide en coulombs por volt o farads. La unidad farad (F) recibe ese nombre en honor al famosos físico inglés Michael Faraday. Los capacitores pueden ser fijos o variables, y normalmente están en el rango de miles de microfaradas (μF) a unos cuantos picofarads (pF).

Por la física básica se sabe que la capacitancia de dos placas paralelas de área $A$ separadas por una distancia $d$ es

$\displaystyle C= \frac{\varepsilon_o A}{d}$

donde $\varepsilon_o = 8.85 \times 10^{-12} \ F/m$ es la permitividad del espacio libre, $d$ es la distancia entre las placas y $A$ es el área de cada placa.

Ahora, suponiendo que un capacitor se conecta a una fuente de voltaje (figura 3), esto harán que se transfieren cargas positivas a una placa y negativas a la otra.

La carga en el capacitor es proporcional al voltaje en sus extremos, de tal modo que

$\displaystyle q = Cv$

donde $C$ es el factor de proporcionalidad conocido como capacitancia del elemento en farads.

La diferencial de carga entre las placas crea un campo eléctrico que almacena energía. La corriente de conducción que fluye en los alambres que conectan al capacitor con el resto del circuito no puede circular internamente entre las placas, debido a la presencia del dieléctrico. Sin embargo, por la teoría del campo electromagnético se puede demostrar que esta corriente de conducción es igual a la corriente de desplazamiento que fluye entre las placas del capacitor y está presente siempre que un campo eléctrico o voltaje varía con el tiempo.

El interés principal está en las características de terminal corriente-voltaje del capacitor. Puesto que la corriente es

$\displaystyle i = \frac{dq}{dt}$

enotnces para un capacitor

$\displaystyle i = \frac{d}{dt} (Cv)$

que, para una capacitancia constante, es

$\displaystyle i = C \frac{dv}{dt}$

que esto puede reescribirse como

$\displaystyle dv = \frac{1}{C} i \ dt$

Integrando desde $t=- \infty$ a algún tiempo $t$ y suponiendo que $v(- \infty) = 0$ , se obtiene

$\displaystyle \int_{- \infty}^{t}{dv(x)} = \frac{1}{C} \int_{- \infty}^{t}{i(x) \ dx}$

$\displaystyle v(t) - v(- \infty) = \frac{1}{C} \int_{- \infty}^{t}{i(x) \ dt}$

$\displaystyle v(t) = \frac{1}{C} \int_{- \infty}^{t}{i(x) \ dt}$

donde $v(t)$ indica la dependencia del tiempo del voltaje. La ecuación anterior se puede expresar con dos integrales, de tal modo que

$\displaystyle v(t) = \frac{1}{C} \int_{- \infty}^{t_0}{i(x) \ dt} + \frac{1}{C} \int_{t_0}^{t}{i(x) \ dt}$

$\displaystyle v(t) = v(t_0) + \frac{1}{C} \int_{t_0}^{t}{i(x) \ dt}$

donde $v(t_0)$ es el voltaje debido a la carga que se acumula en el capacitor desde el tiempo $t = - \infty$ hasta $t=t_0$ .

La energía almacenada en el capacitor se puede derivar a partir de la potencia entregada al elemento. Esta potencia está dada por la expresión

$\displaystyle p(t) = v(t) i(t)$

$\displaystyle p(t) = v(t) \left(C \frac{dv}{dt} \right)$

$\displaystyle p(t) = C v(t) \frac{dv}{dt}$

y por lo tanto la energía almacenada en el campo eléctrico es

$\displaystyle w_c (t) = \int_{-\infty}^{t}{C v(x) \frac{dv(x)}{dx} \ dx}$

$\displaystyle w_c (t) = C \int_{-\infty}^{t}{v(x) \frac{dv(x)}{dx} \ dx}$

$\displaystyle w_c (t) = C \int_{v(-\infty)}^{v(t)}{v(x) \ dv}$

$\displaystyle w_c (t) = C \left[\frac{1}{2} v^2(x) \right]_{v(-\infty)}^{v(t)}$

$\displaystyle w_c (t) = C \left[\frac{1}{2} v^2(t) - \frac{1}{2} v^2(- \infty) \right]$

$\displaystyle w_c (t) = \frac{1}{2} C v^2(t) \ \text{J}$

ya que $v(t=-\infty) = 0$ . La expresión para la energía también puede escribirse como

$\displaystyle w_c (t) = \frac{1}{2} \ \frac{q^2 (t)}{C}$

Estas dos últimas ecuaciones representan la energía almacenada en el capacitor, que a su vez es igual al trabajo realizado por la fuente para cargar dicho capacitor.

La polaridad del voltaje en los extremos de un capacitor que se está cargando se muestra en la figura 3. En el caso ideal, si se remueve la fuente, el capacitor retendrá la carga por un periodo indefinido de tiempo. Si posteriormente se conecta a las terminales del capacitor un dispositivo que absorba energía (por ejemplo, una lámpara de destello), fluirá una corriente de descarga del capacitor y, por lo tanto, éste suministrará al dispositivo la energía acumulada.

Problemas resueltos

Problema 1. Si la carga acumulada en dos conductores paralelos conectados a 12 V es de 600 pC, ¿cuál es la capacitancia de dichos conductores?

Solución. Utilizando la ecuación

$\displaystyle q = Cv \rightarrow Q = C V$

$\displaystyle C = \frac{Q}{V}$

$\displaystyle C = \frac{600 \times 10^{-12}}{12} = 50 \times 10^{-12}$

$\displaystyle \therefore C = 50 \ \text{pF}$

Problema 2. El voltaje en los extremos de un capacitor de 5 μF tiene la forma de onda que se muestra en la figura 4.

a) Determinar la forma de onda de la corriente.
b) Determinar la energía almacenada por el campo eléctrico del capacitor en $t=6 \ \text{ms}$ .

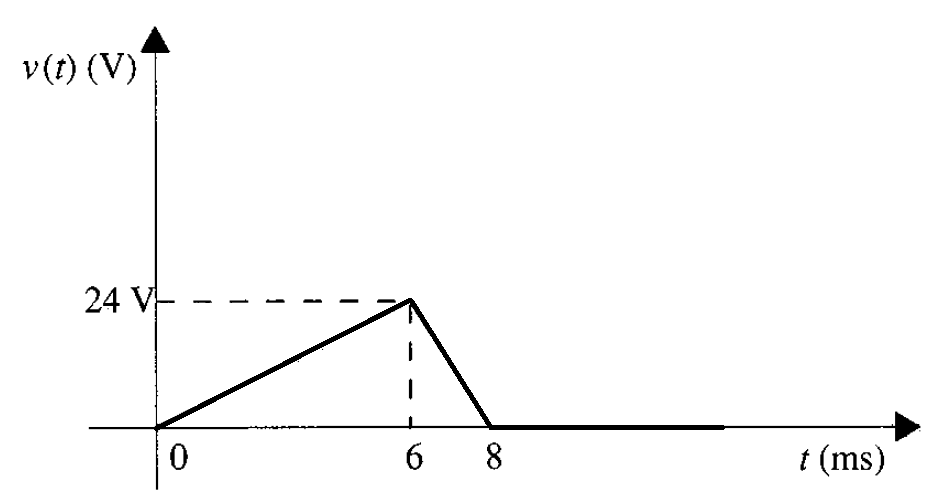
Solución del a). Se determina el voltaje en cada intervalo

\displaystyle v(t) - v(0 \ \text{ms}) = \frac{v(6 \ \text{ms}) - v(0 \ \text{ms})}{6 \ \text{ms} - 0 \ \text{ms}}(t - 0 \ \text{ms})

Sustituyendo en la siguiente ecuación, resulta que en el intervalo $0 \ \text{ms} \le t \le 6 \ \text{ms}$ , la corriente es

$\displaystyle i(t) = C \frac{dv(t)}{dt}$

$\displaystyle i(t) = (5 \mu) \frac{d}{dt} \left[4t \times 10^3 \right]$

$\displaystyle i(t) = (5 \times 10^{-6}) (4 \times 10^3) = 20 \times 10^{-3}$

$\displaystyle i(t) = 20 \ \text{mA}$

En el intervalo $6 \ \text{ms} \le t \le 8 \ \text{ms}$ , la corriente es

$\displaystyle i(t) = C \frac{dv(t)}{dt}$

$\displaystyle i(t) = (5 \mu) \frac{d}{dt} \left[-12 \times 10^{3}(t) + 96 \times 10^{-3} \right]$

$\displaystyle i(t) = (5 \times 10^{-6}) (-12 \times 10^3) = - 60 \times 10^{-3}$

$\displaystyle i(t) = -60 \ \text{mA}$

En el intervalo $8 \ \text{ms} \le t$ , la corriente es

$\displaystyle i(t) = C \frac{dv(t)}{dt}$

$\displaystyle i(t) = (5 \mu) \frac{d}{dt} (0)$

$\displaystyle i(t) = (5 \times 10^{-6}) (0)$

$\displaystyle i(t) = 0 \ \text{mA}$

Con estos valores de la corriente obtenidos en cada intervalo, se construye la forma de onda de la corriente (figura 5); además, $i(t)=0$ para $t > 8 \ \text{ms}$ .

Figura 5. Forma de onda de la corriente para un capacitor de 5 μF.

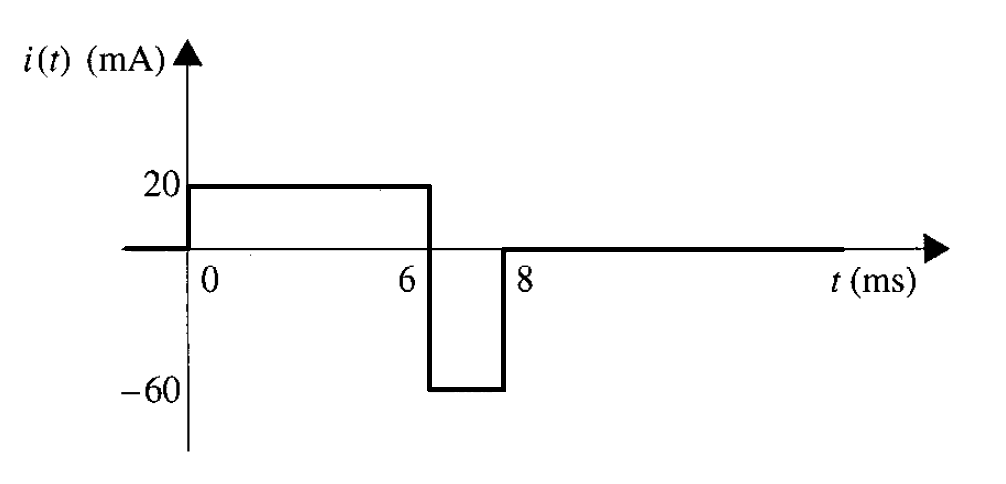
Solución del b). Tomando la siguiente ecuación y sustituyendo

$\displaystyle w (t) = \frac{1}{2} C v^2(t)$

$\displaystyle w (6 \ \text{ms}) = \frac{1}{2} (5 \times 10^{-6}) (24)^2 = 1440 \times 10^{-6}$

$\displaystyle \therefore w (6 \ \text{ms}) = 1440 \ \mu \text{J}$

Problema 3. La figura 6 muestra la corriente en un capacitor de 4 μF inicialmente descargado. Derivar las formas de onda para el voltaje, la potencia y la energía, y calcule la energía almacenada por el campo eléctrico del capacitor en $t=2 \ \text{ms}$ .

Figura 6. Forma de onda de la corriente del capacitor de 4 μF.

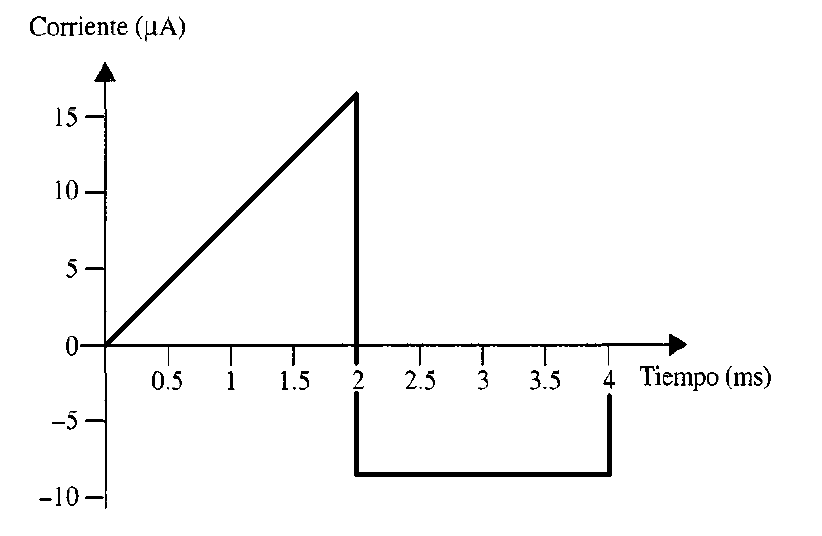
Solución. Las ecuaciones para la forma de onda de la corriente en los intervalos específicos son

\displaystyle i(t) - i(0 \ \text{ms}) = \frac{i(2 \ \text{ms}) - i(0 \ \text{ms})}{2 \ \text{ms} - 0 \ \text{ms}}(t - 0 \ \text{ms})

Después, tomando la ecuación del voltaje del capacitor

$\displaystyle v(t) = v (t_0) + \frac{1}{C} \int_{t_0}^{t}{i(x) \ dx}$

se sustituye dentro del intervalo $0 \ \text{ms} \le t \le 2 \ \text{ms}$ cuyo resultado es

$\displaystyle v(t) = v (0 \ \text{ms}) + \frac{1}{4 \ \mu} \int_{0 \ \text{ms}}^{t}{(8x \times 10^{-3}) \ dx}$

$\displaystyle v(t) = 0 + \frac{8 \times 10^{-3}}{4 \times 10^{-6}} \int_{0 \times 10^{-3}}^{t}{x \ dx} = (2 \times 10^{3}) \left( \frac{1}{2} t^2 - \frac{1}{2} 0^2 \right)$

$\displaystyle v(t) = (1 \times 10^{3}) t^2 \ \text{V}$

En el intervalo $2 \ \text{ms} \le t \le 4 \ \text{ms}$ , el voltaje del capacitor es

$\displaystyle v(t) = v (2 \ \text{ms}) + \frac{1}{4 \ \mu} \int_{2 \ \text{ms}}^{t}{(- 8 \times 10^{-6}) \ dx}$

$\displaystyle v(t) = (1 \times 10^{3}) (2 \times 10^{-3})^2 - \frac{8 \times 10^{-6}}{4 \times 10^{-6}} \int_{2 \times 10^{-3}}^{t}{dx}$

$\displaystyle v(t) = 4 \times 10^{-3} - 2 \int_{2 \times 10^{-3}}^{t}{dx}$

$\displaystyle v(t) = 4 \times 10^{-3} - 2 (t - 2 \times 10^{-3}) = 4 \times 10^{-3} - 2t + 4 \times 10^{-3})$

$\displaystyle v(t) = - 2t + 8 \times 10^{-3} \ \text{V}$

En el intervalo $4 \ \text{ms} < t$ , el voltaje del capacitor es

$\displaystyle v(t) = v (4 \ \text{ms}) + \frac{1}{4 \ \mu} \int_{4 \ \text{ms}}^{t}{(0) \ dx}$

$\displaystyle v(t) = 0 \ \text{V}$

Los resultados del voltaje obtenidos en cada intervalo, se tiene la forma de onda mostrada en la figura 7.

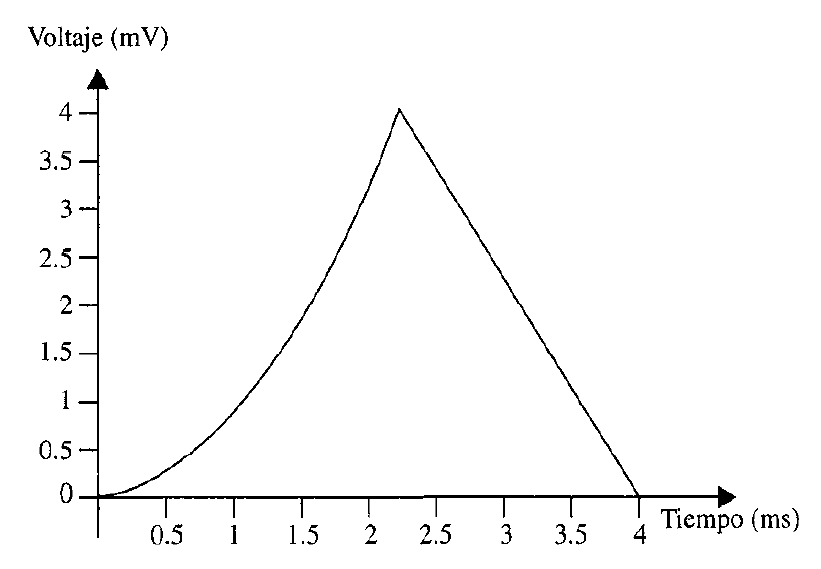
Figura 7. Forma de onda del voltaje del capacitor.

Ahora, tomando la ecuación de la potencia

$\displaystyle p(t) = v(t) i(t)$

se sustituye para el intervalo $0 \ \text{ms} \le t \le 2 \ \text{ms}$ cuyo resultado es

$\displaystyle p(t) = v(t) i(t)$

$\displaystyle p(t) = \left[(1 \times 10^{3}) t^2 \right] (8t \times 10^{-3})$

$\displaystyle p(t) = 8 t^3 \ \text{W}$

En el intervalo $2 \ \text{ms} \le t \le 4 \ \text{ms}$ , la potencia es

$\displaystyle p(t) = v(t) i(t)$

$\displaystyle p(t) = (- 2t + 8 \times 10^{-3}) (- 8 \times 10^{-6})$

$\displaystyle p(t) = (16 \times 10^{-6}) t - 64 \times 10^{-9} \ \text{W}$

En el intervalo $4 \ \text{ms} < t$ , la potencia es

$\displaystyle p(t) = v(t) i(t)$

$\displaystyle p(t) = (0) (0)$

$\displaystyle p(t) = 0 \ \text{W}$

La forma de onda de onda del capacitor se muestra en la figura 8. Se observa que durante el intervalo $0 \ \text{ms} \le t \le 2 \ \text{ms}$ el capacitor absorbe energía, mientras que en $2 \ \text{ms} \le t \le 4 \ \text{ms}$ entrega energía.

Figura 8. Forma de onda de la potencia del capacitor.

La energía se obtiene mediante la expresión

$\displaystyle w(t) = w(t_0) + \int_{t_0}^t{p(x) \ dx}$

En el intervalo $0 \ \text{ms} \le t \le 2 \ \text{ms}$ , la energía tiene el siguiente resultado

$\displaystyle w(t) = w(0 \ \text{ms}) + \int_{0 \ \text{ms}}^t{8 x^3 \ dx}$

$\displaystyle w(t) = 0 + 8 \int_{0 \times 10^{-3}}^t{x^3 \ dx}$

$\displaystyle w(t) = 8 \left[\frac{1}{4} x^4 + C \right]_{0 \times 10^{-3}}^t = 8 \left(\frac{1}{4} t^4 -0 \right)$

$\displaystyle w(t) = 2 t^4 \ \text{J}$

En el intervalo $2 \ \text{ms} \le t \le 4 \ \text{ms}$ , la energía tiene el siguiente resultado

$\displaystyle w(t) = w(2 \ \text{ms}) + \int_{2 \ \text{ms}}^t{\left[(16 \times 10^{-6}) x - 64 \times 10^{-9} \right] dx}$

$\displaystyle w(t) = 2 (2 \times 10^{-3})^4 + \int_{2 \times 10^{-3}}^t{\left[(16 \times 10^{-6}) x - 64 \times 10^{-9} \right] dx}$

$\displaystyle w(t) = 2 (16 \times 10^{-12}) + \left[(16 \times 10^{-6}) \left(\frac{1}{2} x^2 \right) - (64 \times 10^{-9}) x + C \right]_{2 \times 10^{-3}}^{t}$

$\displaystyle w(t) = 32 \times 10^{-12} + \left[(8 \times 10^{-6}) x^2 - (64 \times 10^{-9}) x + C \right]_{2 \times 10^{-3}}^{t}$

$\displaystyle w(t) = 32 \times 10^{-12} + \left\{\left[(8 \times 10^{-6}) t^2 - (64 \times 10^{-9}) t \right] - \left[(8 \times 10^{-6}) (2 \times 10^{-3})^2 - (64 \times 10^{-9}) (2 \times 10^{-3}) \right] \right\}$

$\displaystyle w(t) = 32 \times 10^{-12} + \left\{\left[(8 \times 10^{-6}) t^2 - (64 \times 10^{-9}) t \right] - \left[(8 \times 10^{-6}) (4 \times 10^{-6}) - (64 \times 10^{-9}) (2 \times 10^{-3}) \right] \right\}$

$\displaystyle w(t) = 32 \times 10^{-12} + \left\{\left[(8 \times 10^{-6}) t^2 - (64 \times 10^{-9}) t \right] - \left(32 \times 10^{-12} - 128 \times 10^{-12} \right) \right\}$

$\displaystyle w(t) = 32 \times 10^{-12} + \left[(8 \times 10^{-6}) t^2 - (64 \times 10^{-9}) t + 96 \times 10^{-12} \right]$

$\displaystyle w(t) = (8 \times 10^{-6}) t^2 - (64 \times 10^{-9}) t + (128 \times 10^{-12}) \ \text{J}$

En el intervalo $4 \ \text{ms} < t$ , la energía tiene el siguiente resultado

$\displaystyle w(t) = 0 \ \text{J}$

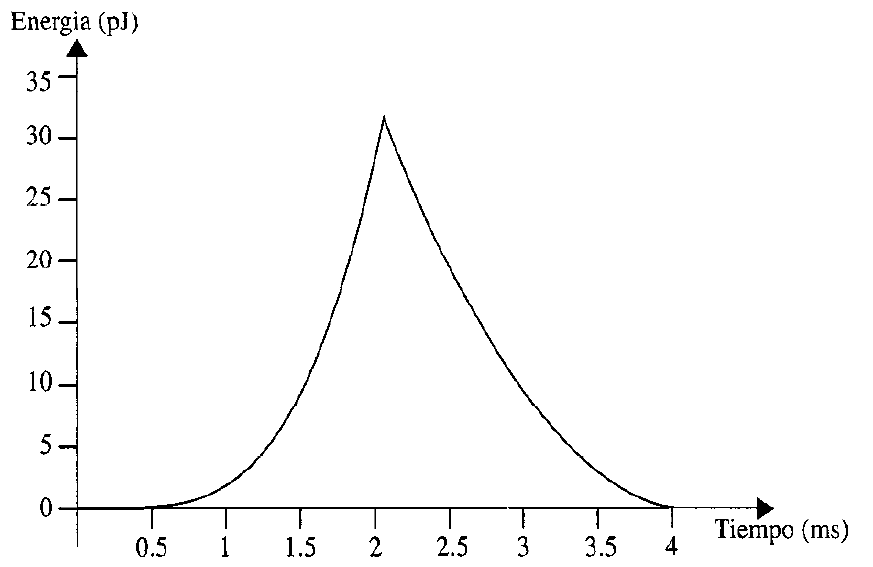
La forma de onda de la energía se muestra en la figura 9.

En el intervalo $0 \le t \le 6 \ \text{ms}$		$\displaystyle v(t) - v(0 \ \text{ms}) = \frac{v(6 \ \text{ms}) - v(0 \ \text{ms})}{6 \ \text{ms} - 0 \ \text{ms}}(t - 0 \ \text{ms})$ $\displaystyle v(t) - 0 = \frac{24 - 0}{6 \ \text{m} - 0 \ \text{m}}(t - 0)$ $\displaystyle v(t) - 0 = \frac{24 - 0}{6 \times 10^{-3} - 0 \times 10^{-3}}(t - 0)$ $\displaystyle v(t) = \frac{24}{6 \times 10^{-3}}(t)$ $\displaystyle v(t) = 4t \times 10^3 \ \text{V}$
En el intervalo $6 \ \text{ms} \le t < 8 \ \text{ms}$		$\displaystyle v(t) - v(6 \ \text{ms}) = \frac{v(8 \ \text{ms}) - v(6 \ \text{ms})}{8 \ \text{ms} - 6 \ \text{ms}}(t - 6 \ \text{ms})$ $\displaystyle v(t) - 24 = \frac{0 - 24}{8 \ \text{m} - 6 \ \text{m}}(t - 6 \ \text{m})$ $\displaystyle v(t) - 24 = \frac{0 - 24}{8 \times 10^{-3} - 6 \ \times 10^{-3}}(t - 6 \times 10^{-3})$ $\displaystyle v(t) = 24 - \frac{24}{2 \times 10^{-3}}(t - 6 \times 10^{-3})$ $\displaystyle v(t) = 24 -12 \times 10^{3}(t - 6 \times 10^{-3})$ $\displaystyle v(t) = 24 -12 \times 10^{3}(t) + 72$ $\displaystyle v(t) = -12 \times 10^3 (t) + 96 \ \text{V}$
En el intervalo $8 \ \text{ms} \le t$		$\displaystyle v(t) - v(8 \ \text{ms}) = \frac{0 - 0}{t - 8 \times 10^{-3}}(t - 8 \times 10^{-3})$ $\displaystyle v(t) = 0 \ \text{V}$

En el intervalo $0 \le t \le 2 \ \text{ms}$		$\displaystyle i(t) - i(0 \ \text{ms}) = \frac{i(2 \ \text{ms}) - i(0 \ \text{ms})}{2 \ \text{ms} - 0 \ \text{ms}}(t - 0 \ \text{ms})$ $\displaystyle i(t) - 0 \ \mu = \frac{16 \ \mu - 0 \ \mu}{2 \ \text{m} - 0 \ \text{m}}(t - 0 \ \text{m})$ $\displaystyle i(t) - 0 = \frac{16 \times 10^{-6} - 0 \times 10^{-6}}{2 \times 10^{-3} - 0 \times 10^{-3}}(t - 0 \times 10^{-3})$ $\displaystyle i(t) - 0 = \frac{16}{2}(t) \times 10^{-3}$ $\displaystyle i(t) = 8t \times 10^{-3} \ \text{A} = 8t \ \text{mA}$
En el intervalo $2 \ \text{ms} \le t < 4 \ \text{ms}$		$\displaystyle i(t) - i(2 \ \text{ms}) = \frac{i(4 \ \text{ms}) - i(4 \ \text{ms})}{4 \ \text{m} - 2 \ \text{m}}(t - 2 \ \text{m})$ $\displaystyle i(t) - (-8 \ \mu) = \frac{(-8\ \mu) - (-8 \ \mu)}{4 \ \text{m} - 2 \ \text{m}}(t - 2 \ \text{m})$ $\displaystyle i(t) - (-8 \times 10^{-6}) = \frac{(-8 \times 10^{-6}) - (-8 \times 10^{-6})}{4 \times 10^{-3} - 2 \times 10^{-3}}(t - 2 \times 10^{-3})$ $\displaystyle i(t) + 8 \times 10^{-6} =(0)(t - 2 \times 10^{-3})$ $\displaystyle i(t) = - 8 \times 10^{-6} \ \text{A} = - 8 \ \mu \text{A}$
En el intervalo $4 \ \text{ms} \le t$		$\displaystyle i(t) - i(4 \ \text{ms}) = \frac{0 - 0}{t - 4 \ \text{ms}}(t - 4 \ \text{ms})$ $\displaystyle i(t) = 0 \ \text{A}$

Capacitores. Circuitos eléctricos.

Introducción

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Capacitores. Circuitos eléctricos.

Introducción

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta