Inductores. Circuitos eléctricos.

Introducción

Un inductor es un elemento de circuito que consiste en un alambre conductor normalmente en forma de un arrollamiento. La figura 1 muestra dos inductores típicos y su símbolo eléctrico. Usualmente los inductores se clasifican por el tipo de núcleo en el cual están enrollados. Por ejemplo, el núcleo puede ser de aire o cualquier material no magnético, hierro o ferrita. Los inductores hechos con aire o materiales no magnéticos se utilizan ampliamente en radio, televisión y circuitos de filtro. Los inductores con núcleo de hierro se usan en fuentes de alimentación y filtros, mientras que los inductores de núcleo de núcleo de ferrita se utilizan en aplicaciones de alta frecuencia. Se observa que las líneas de flujo en los inductores no magnéticos se extienden más allá del propio inductor, en contraste con el núcleo magnético que confina las líneas de flujo. Al igual que la capacitancia parásita, cualquier elemento que conduzca corriente rodeado por líneas de flujo puede producir inductancia parásita. La figura 2 muestra diversos inductores típicos.

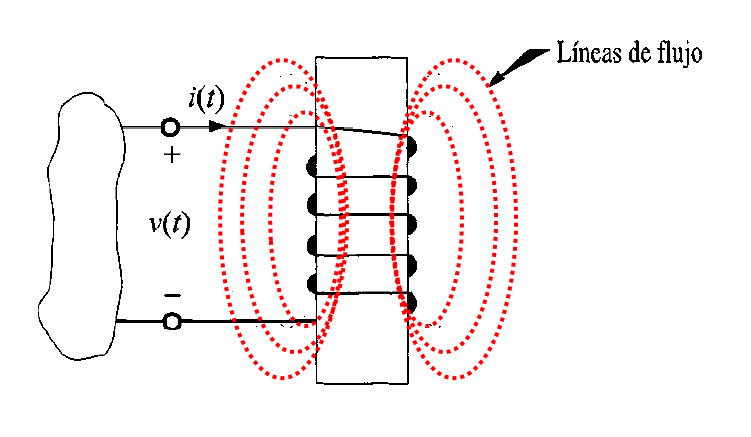
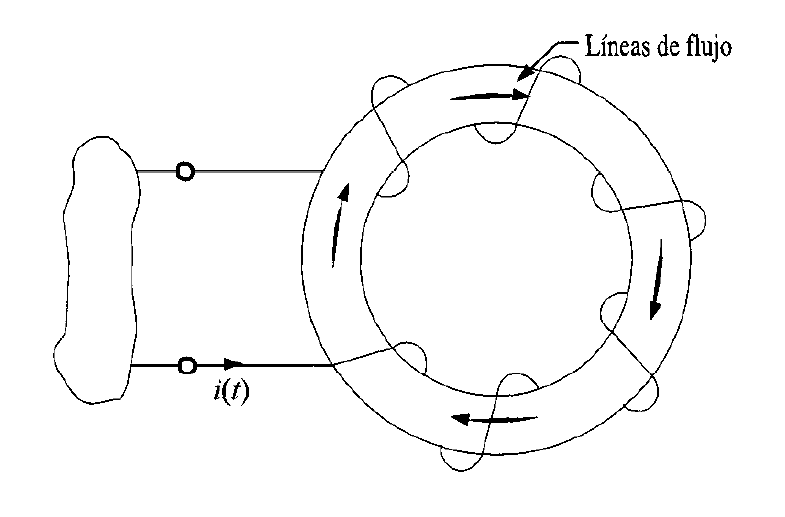
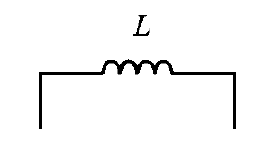
Figura 1. El inductor, su comportamiento ante las lineas de flujo y su símbolo eléctrico.

Figura 2. Diversos inductores.

Desde un punto de vista histórico, los desarrollos que han llevado al modelo matemático empleado hoy en día para representar al inductor son los siguientes. Primero se demostró que un conductor que transporta corriente origina un campo magnético. Posteriormente se encontró que el campo magnético y la corriente que lo produce están relacionados linealmente. Por último, se mostró que un campo magnético cambiante genera un voltaje proporcional a la razón de cambio en el tiempo de la corriente que produce el campo magnético; esto es,

$\displaystyle v(t) = L \frac{di(t)}{dt}$

La constante de proporcionalidad $L$ se denomina inductancia y se mide en la unidad henry, llamada así en honor del inventor estadounidense Joseph Henry, quién descubrió la relación. Un henry (H) es dimensionalmente igual a 1 volt-segundo por ampere.

Continuando, la corriente en un inductor es

$\displaystyle i(t) = \frac{1}{L} \int_{- \infty}^{t}{v(x) \ dx}$

que también puede escribirse como

$\displaystyle i(t) = i(t_0) + \frac{1}{L} \int_{- \infty}^{t}{v(x) \ dx}$

La potencia entregada al inductor puede usarse derivando la energía almacenada en el elemento. Esta potencia es

$\displaystyle p(t) = v(t) i(t)$

$\displaystyle p(t) = \left[L \frac{di(t)}{dt} \right] i(t)$

La energía almacenada en el campo magnético es

$\displaystyle w_L (t) = \int_{- \infty}^{t}{p(x) \ dx}$

$\displaystyle w_L (t) = \int_{- \infty}^{t}{\left[L \frac{di(x)}{dx} \right] i(x) \ dx}$

$\displaystyle w_L (t) = L \int_{- \infty}^{t}{i(x) \ di(x)}$

$\displaystyle w_L (t) = \frac{1}{2} Li^2 (t) \ \text{J}$

El inductor es un elemento pasivo, al igual que el resistor y el capacitor. En la figura 3, muestra la polaridad del voltaje en los entremos del inductor.

Figura 3. Conexión del inductor una fuente de voltaje.

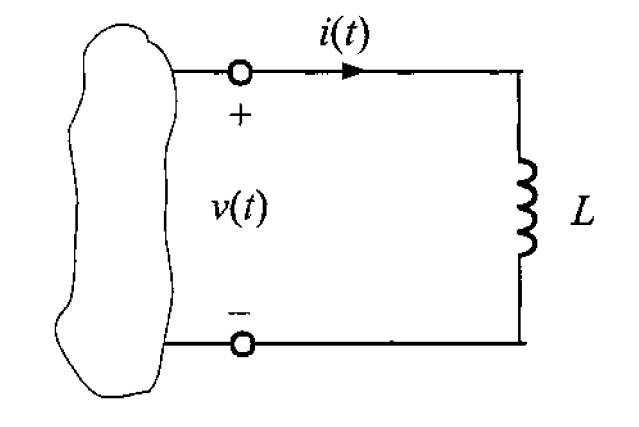
Usualmente, los inductores están en el rango de unos cuantos microhenrys a decenas de henrys. Desde el punto de vista del diseño de circuitos, es importante observar que no es sencillo fabricar inductores sobre una pastilla de circuito integrado y, por lo tanto, los diseños de estos circuitos generalmente emplean sólo dispositivos electrónicos activos, resistores y capacitores, todos los cuales pueden fabricarse fácilmente en forma de microcircuitos.

Problemas resueltos

Problema 1. La corriente en un inductor de 2 mH es $i(t) = 2 \sin{377t} \ \text{A}$ . Determine la energía almacenada y el voltaje en los extremos del inductor.

Solución. Utilizando la ecuación para calcular el voltaje de un inductor y sustituyendo, resulta

$\displaystyle v(t) = L \frac{di(t)}{dt}$

$\displaystyle v(t) = (2 \ \text{m}) \frac{d}{dt} (2 \sin{377t})$

$\displaystyle v(t) = (2 \times 10^{-3}) (754 \cos{377t})$

$\displaystyle \therefore v(t) = 1508 \cos{377t} \ \text{V}$

Y tomando la ecuación para calcular la energía almacenada, resulta que

$\displaystyle w_L (t) = \frac{1}{2} L i^2 (t)$

$\displaystyle w_L (t) = \frac{1}{2} (2 \ \text{m}) {(2 \sin{377t})}^2$

$\displaystyle w_L (t) = \frac{1}{2} (2 \times 10^{-3}) (4 \sin^2{377t})$

$\displaystyle \therefore w_L (t) = 0.004 \sin^2{377t} \ \text{J}$

Problema 2. La figura 4 muestra la forma de onda de la corriente en un inductor de 10 mH. Determine la forma de onda del voltaje.

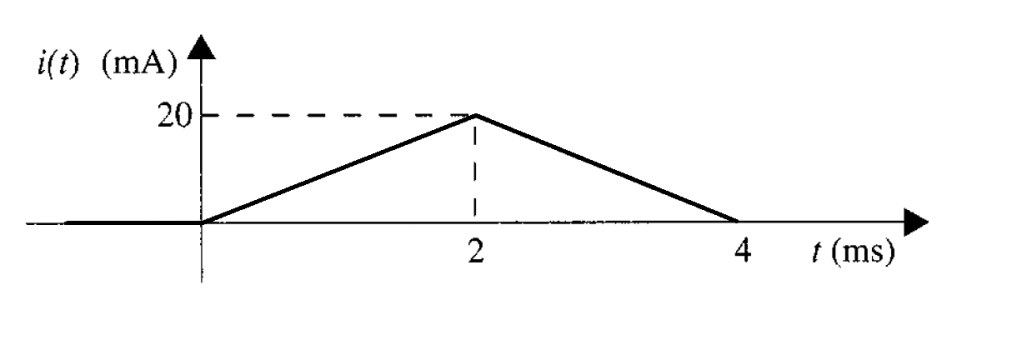
Figura 4. Forma de onda de la corriente del inductor de 10 mH.

Solución. Se determinan las ecuaciones de corriente con la forma de onda de la figura 4 en cada intervalo dado.

\displaystyle i(t) - i(0 \ \text{ms}) = \frac{i(2 \ \text{ms}) - i(0 \ \text{ms})}{2 \ \text{ms} - 0 \ \text{ms}} (t - 0 \ \text{ms})

Utilizando la siguiente ecuación

$\displaystyle v(t) = L \frac{di(t)}{dt}$

Se determina la corriente en cada intervalo. En el intervalo $0 \ \text{ms} \le t \ 2 \ \text{ms}$ , el voltaje del inductor es

$\displaystyle v(t) = (10 \text{m}) \frac{d}{dt} \left[(10t) \right]$

$\displaystyle v(t) = (10 \times 10^{-3}) (10) = 100 \times 10^{-3}$

$\displaystyle v(t) = 100 \ \text{mV}$

En el intervalo $2 \ \text{ms} \le t \ 4 \ \text{ms}$ , el voltaje del inductor es

$\displaystyle v(t) = (10 \text{m}) \frac{d}{dt} \left[40 \times 10^{-3} - 10 t \right]$

$\displaystyle v(t) = (10 \times 10^{-3}) (-10) = - 100 \times 10^{-3}$

$\displaystyle v(t) = - 100 \ \text{mV}$

Y en el intervalo $t > 4 \ \text{ms}$ , el voltaje del inductor es

$\displaystyle v(t) = (10 \text{m}) \frac{d}{dt} \left[0 \right]$

$\displaystyle v(t) = (10 \times 10^{-3}) (0)$

$\displaystyle v(t) = 0 \ \text{V}$

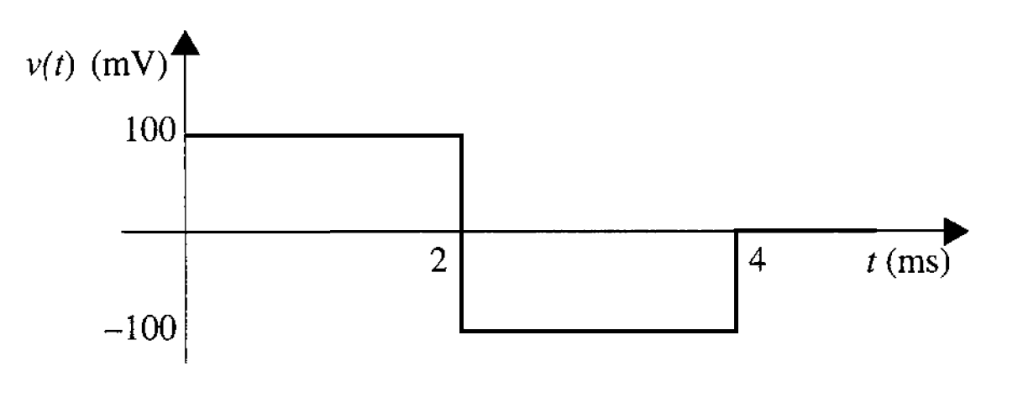
Con los resultados del voltaje inductor obtenidos en cada intervalo, se tiene la forma de onda mostrado en la figura 5.

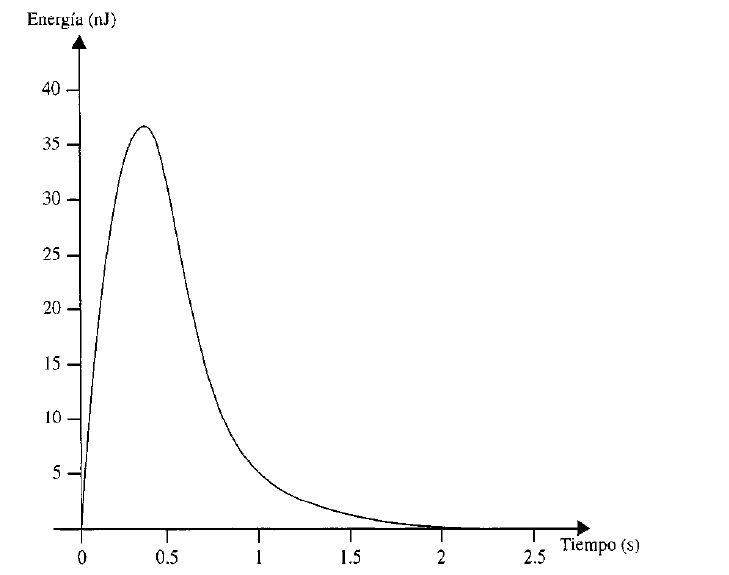
Figura 5. Forma de onda del voltaje del inductor de 10 mH.

Problema 3. El voltaje en un inductor de 20 mH se obtiene por la expresión

$\displaystyle v(t) = \left\{\begin{matrix} (1 - 3t)e^{-3t} \ \text{mV} & t \ge 0 \\ 0 & t < 0\end{matrix} \right.$

Derivar las formas de onda para la corriente, la energía y la potencia.

Solución. Para determinar la corriente de un inductor, se utiliza la siguiente fórmula

$\displaystyle i(t) = \frac{1}{L} \int_{- \infty}^{t}{v(x) \ dx}$

Entonces,

$\displaystyle i(t) = \frac{1}{20 \ \text{m}} \left[\int_{- \infty}^{0}{0 \ dx} + \int_{0}^{t}{(1 - 3x)e^{-3x} \ \text{m} \ dx} \right]$

$\displaystyle i(t) = \frac{1}{20 \times 10^{-3}} \int_{0}^{t}{(1 - 3x)e^{-3x} \times 10^{-3} \ dx} = \frac{1 \times 10^{-3}}{20 \times 10^{-3}} \int_{0}^{t}{(1 - 3x)e^{-3x} \ dx}$

$\displaystyle i(t) = \frac{1}{20} \int_{0}^{t}{(1 - 3x)e^{-3x} \ dx}$

$\displaystyle i(t) = \frac{1}{20} te^{-3t} = 0.005 te^{-3t} = 5 te^{-3t} \times 10^{-3}$

$\displaystyle i(t) = 5 te^{-3t} \ \text{mA}$

Por esta parte, se concluye que en el intervalo $t<0$ la corrientes es $i(t)=0 \ \text{A}$ y en el intervalo $t \ge 0$ la corriente $\displaystyle i(t) = 5 te^{-3t} \ \text{mA}$ . Esto es

$\displaystyle i(t) = \left\{\begin{matrix} 5 te^{-3t} \ \text{mA} & t \ge 0 \\ 0 & t < 0\end{matrix} \right.$

La forma de onda resultante, se muestra en la figura 6.

Figura 6. Forma de onda de la corriente del inductor de 20 mH.

Para calcular la potencia, se utiliza la siguiente fórmula

$\displaystyle p(t) = v(t) i(t)$

En el intervalo $t<0$ , la potencia es

$\displaystyle p(t) = (0) (0)$

$\displaystyle p(t) = 0 \ \text{W}$

En el intervalo $t \ge 0$ , la potencia es

$\displaystyle p(t) = ((1 - 3t)e^{-3t} \ \text{m}) (5 te^{-3t} \ \text{m})$

$\displaystyle p(t) = [(1 - 3t)e^{-3t} \times 10^{-3}] (5 te^{-3t} \times 10^{-3})$

$\displaystyle p(t) = 5(1 - 3t)e^{-6t} \times 10^{-6}$

$\displaystyle p(t) = 5(1 - 3t)e^{-6t} \ \mu \text{W}$

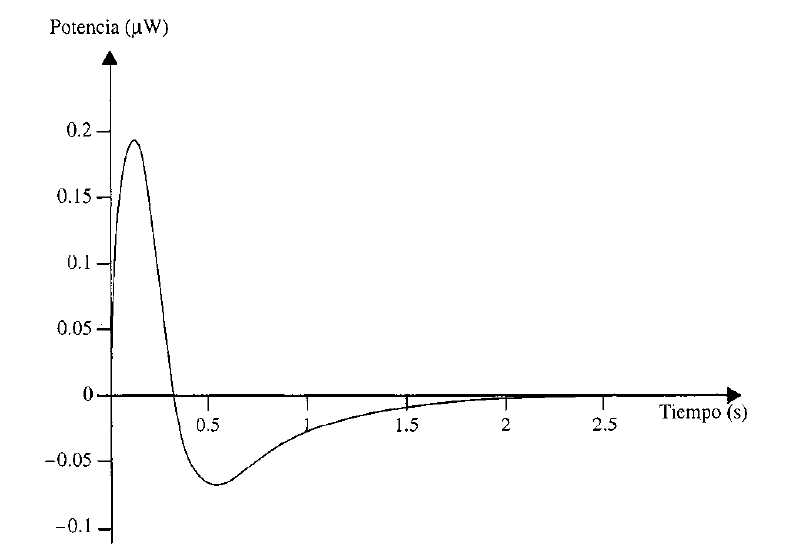
con estos resultados de la potencia, se tiene que

$\displaystyle p(t) = \left\{\begin{matrix} 5(1 - 3t)e^{-6t} \ \mu \text{W} & t \ge 0 \\ 0 & t < 0\end{matrix} \right.$

la forma de onda de la potencia se muestra en la figura 7.

Figura 7. Forma de onda de la potencia del inductor de 20 mH.

La siguiente fórmula ayudará a calcular la energía del inductor

$\displaystyle w(t) = \frac{1}{2} L i^2 (t)$

En el intervalo $t<0$ , la energía es

$\displaystyle w(t) = \frac{1}{2} (20 \times 10^{-3}) (0)^2$

$\displaystyle w(t) = 0 \ \text{J}$

Y en el intervalo $t \ge 0$ , la energía es

$\displaystyle w(t) = \frac{1}{2} (20 \times 10^{-3}) (5 te^{-3t} \ \text{m})^2$

$\displaystyle w(t) = \frac{1}{2} (20 \times 10^{-3}) (5 te^{-3t} \times 10^{-3})^2$

$\displaystyle w(t) = \frac{1}{2} (20 \times 10^{-3}) (25 t^2e^{-6t} \times 10^{-6})$

$\displaystyle w(t) = 2.5 t^2 e^{-6t} \times 10^{-6}$

$\displaystyle w(t) = 2.5 t^2 e^{-6t} \ \mu \text{J}$

con estos resultados de la energía, se tiene que

$\displaystyle w(t) = \left\{\begin{matrix} 2.5 t^2 e^{-6t} \ \mu \text{J} & t \ge 0 \\ 0 & t < 0\end{matrix} \right.$

La forma de onda de la energía del inductor se muestra en la figura 8.

En el intervalo $0 \ \text{ms} \le t \ 2 \ \text{ms}$	$\displaystyle i(t) - i(0 \ \text{ms}) = \frac{i(2 \ \text{ms}) - i(0 \ \text{ms})}{2 \ \text{ms} - 0 \ \text{ms}} (t - 0 \ \text{ms})$ $\displaystyle i(t) - 0 \ \text{m} = \frac{20 \ \text{m} - 0 \ \text{m}}{2 \ \text{m} - 0 \ \text{m}} (t - 0 \ \text{m})$ $\displaystyle i(t) - 0 \times 10^{-3} = \frac{20 \times 10^{-3} - 0 \times 10^{-3}}{2 \times 10^{-3} - 0 \times 10^{-3}} (t - 0 \times 10^{-3})$ $\displaystyle i(t) = \frac{20 \times 10^{-3}}{2 \times 10^{-3}} (t)$ $\displaystyle i(t) = 10t \ \text{A}$
En el intervalo $2 \ \text{ms} \le t \ 4 \ \text{ms}$	$\displaystyle i(t) - i(2 \ \text{ms}) = \frac{i(4 \ \text{ms}) - i(2 \ \text{ms})}{4 \ \text{ms} - 2 \ \text{ms}} (t - 2 \ \text{ms})$ $\displaystyle i(t) - 20 \ \text{m} = \frac{0 \ \text{m} - 20 \ \text{m}}{4 \ \text{m} - 2 \ \text{m}} (t - 2 \ \text{m})$ $\displaystyle i(t) - 20 \ \times 10^{-3} = \frac{0 \times 10^{-3} - 20 \times 10^{-3}}{4 \times 10^{-3} - 2 \times 10^{-3}} (t - 2 \times 10^{-3})$ $\displaystyle i(t) = 20 \ \times 10^{-3} + \frac{-20 \times 10^{-3}}{2 \times 10^{-3}} (t - 2 \times 10^{-3})$ $\displaystyle i(t) = 20 \ \times 10^{-3} - (10) (t - 2 \times 10^{-3})$ $\displaystyle i(t) = 20 \ \times 10^{-3} - 10 t + (20 \times 10^{-3})$ $\displaystyle i(t) = 40 \times 10^{-3} - 10 t \ \text{A}$
En el intervalo $4 \ \text{ms} < t$	$\displaystyle i(t) = 0 \ \text{A}$

Inductores. Circuitos eléctricos.

Introducción

Problemas resueltos

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Inductores. Circuitos eléctricos.

Introducción

Problemas resueltos

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta