Capacitores en paralelo. Circuitos eléctricos.

Introducción

Para determinar la capacitancia de $N$ capacitores conectados en paralelo se emplea la LKC y las figura 1 y 2.

$\displaystyle \sum_{j=1}^n{i_j (t)} = 0$

$\displaystyle -i(t) + i_1 (t) + i_2 (t) + i_3 (t) + \cdots + i_N (t) = 0$

$\displaystyle i(t) = i_1 (t) + i_2 (t) + i_3 (t) + \cdots + i_N (t)$

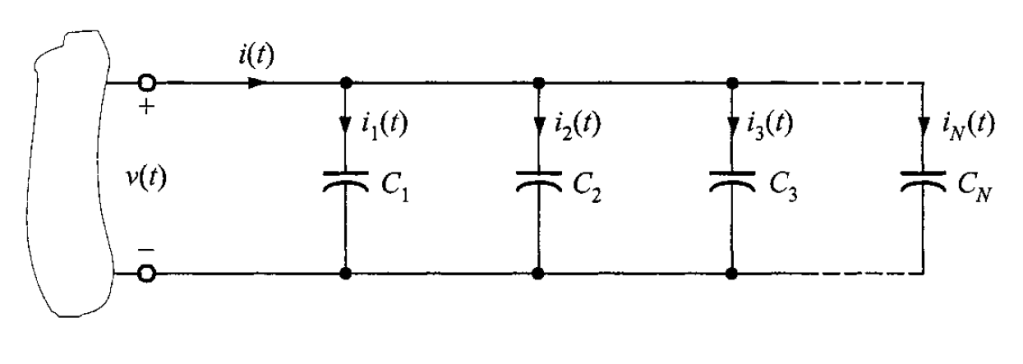
La fórmula para calcular la corriente de un capacitor es

$\displaystyle i_j(t) = C_j \frac{dv(t)}{dt}$

Sustituyendo en la ecuación anterior, resulta

$\displaystyle i(t) = C_1 \frac{dv(t)}{dt} + C_2 \frac{dv(t)}{dt} + C_3 \frac{dv(t)}{dt} + \cdots + C_N \frac{dv(t)}{dt}$

$\displaystyle i(t) = (C_1 + C_2 + C_3 + \cdots + C_N) \frac{dv(t)}{dt}$

$\displaystyle i(t) = \left(\sum_{j=1}^N{C_j} \right) \frac{dv(t)}{dt}$

$\displaystyle i(t) = C_P \frac{dv(t)}{dt}$

donde

\displaystyle C_P = \sum_{j=1}^N{C_j} = C_1 + C_2 + C_3 + \cdots + C_N

Problemas resueltos

Problema 1. Determine la capacitancia equivalente entre las terminales A-B del circuito de la figura 3.

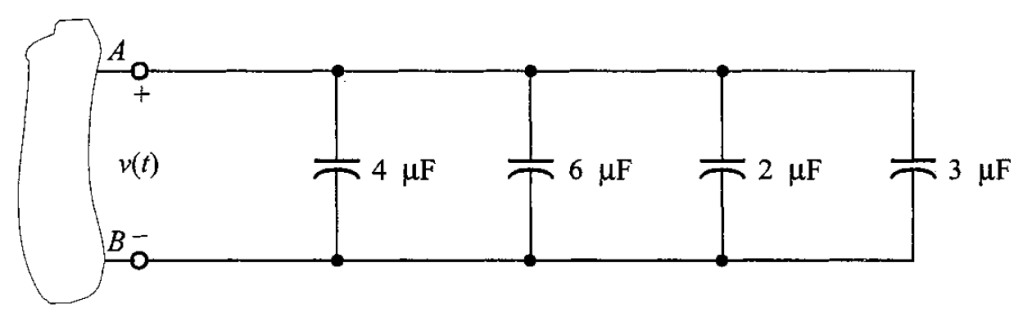
Solución. Se observa en el circuito que todos los capacitores están en paralelo. Calculando la capacitancia equivalente en paralelo, resulta

$\displaystyle C_P = C_1 + C_2 + C_3 + C_4$

$\displaystyle C_P = 4 \ \mu + 6 \ \mu + 2 \ \mu + 3 \ \mu$

$\displaystyle \therefore C_P = 15 \ \mu$

Problema 2. La figura 4 muestra la conexión de dos capacitores inicialmente descargados. El voltaje alcanza el valor mostrado después de cierto periodo de tiempo. Determinar el valor de $C_1$ .

Solución. Sea $C_1$ el valor de la capacitancia y $V_1$ su voltaje; lo mismo ocurre con $C_2$ y $V_2$ para el segundo capacitor. Después, se determina el voltaje del capacitor $V_2$ utilizando la LKV.

$\displaystyle \sum_{j=1}^n{V_j} = 0$

$\displaystyle -24 + V_1 + 6 = 0$

$\displaystyle V_1 = 18 \ \text{V}$

Después, se determina la carga del segundo capacitor.

$\displaystyle Q = C_2 V_2$

$\displaystyle Q = (12 \ \mu)(6) = 72 \ \mu$

$\displaystyle Q = 72 \ \mu \text{C}$

Finalmente, por medio de la fórmula de carga del primer capacitor, se despeja $C_1$ y se obtiene el resultado definitivo.

$\displaystyle Q = C_1 V_1$

$\displaystyle C_1 = \frac{Q}{V_1}$

$\displaystyle C_1 = \frac{72 \ \mu}{18} = 4 \ \mu$

$\displaystyle \therefore C_1 = 4 \ \mu \text{F}$

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web. Ver todas las entradas de Cesar Reyes

Deja un comentario Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.