Inductores en serie. Circuitos eléctricos.

Introducción

Si se conectan en serie $N$ inductores, la inductancia equivalente se calcula como sigue. Con el apoyo de las figuras 1 y 2 y utilizando la LKV, se tiene lo siguiente.

Figura 2. Circuito equivalente para N inductores en serie.

$\displaystyle \sum_{j=1}^n{v_j (t)} = 0$

$\displaystyle -v(t) + v_1 (t) + v_2 (t) + \cdots + v_N (t) = 0$

$\displaystyle v(t) = v_1 (t) + v_2 (t) + \cdots + v_N (t)$

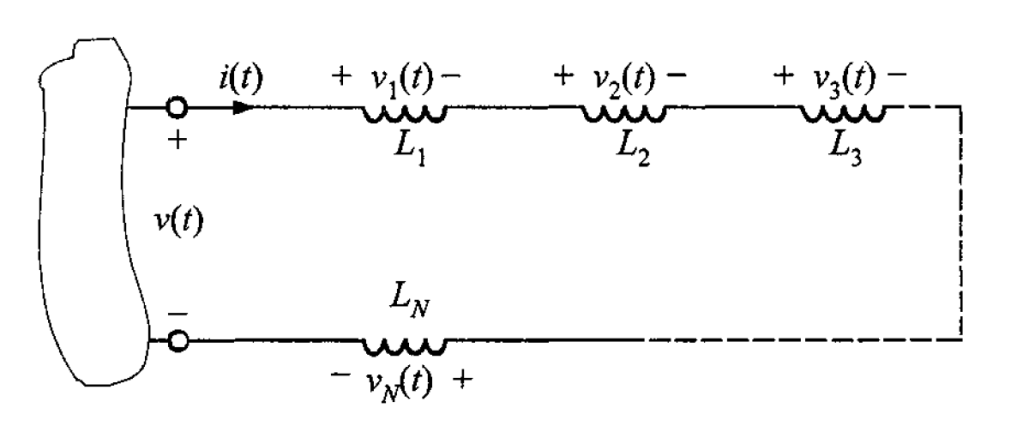
La siguiente ecuación determina el valor del voltaje del inductor

$\displaystyle v_j (t) = L_j \frac{d i(t)}{dt}$

Sustituyendo en la ecuación de desarrollo anterior, resulta

$\displaystyle v(t) = L_1 \frac{d i(t)}{dt} + L_2 \frac{d i(t)}{dt} + \cdots + L_N \frac{d i(t)}{dt}$

$\displaystyle v(t) = \left(L_1 + L_2 + \cdots + L_N \right) \frac{d i(t)}{dt}$

$\displaystyle v(t) = \left(\sum_{j=1}^N{L_j} \right) \frac{d i(t)}{dt}$

$\displaystyle v(t) = L_S \frac{d i(t)}{dt}$

donde

\displaystyle L_S = \sum_{j=1}^N{L_j} = L_1 + L_2 + \cdots + L_N

Problema resuelto

Problema 1. Encuentre la inductancia equivalente del circuito de la figura 3.

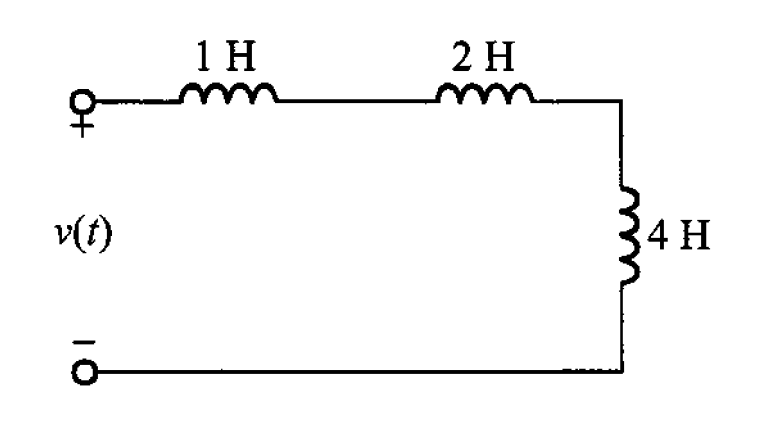
Solución. En este circuito se observa que todos los inductores en serie. Calculando la inductancia en serie

$\displaystyle L_S = L_1 + L_2 + L_3$

$\displaystyle L_S = 1 + 2 + 4$

$\displaystyle \therefore L_S = 7 \ \text{H}$

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web. Ver todas las entradas de Cesar Reyes

Deja un comentario Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.