Introducción
Se considera el circuito de la figura 1, el cual contiene inductores en paralelo. Con la ayuda de las figuras 1 y 2 y la LKC, se obtiene la fórmula para calcular la inductancia en paralelo.


La fórmula para calcular la corriente de un inductor es
sustituyendo en la ecuación de desarrollo anterior, se tiene que
donde
Problema resuelto
Problema 1. Determine la inductancia equivalente y la corriente inicial para el circuito de la figura 3.
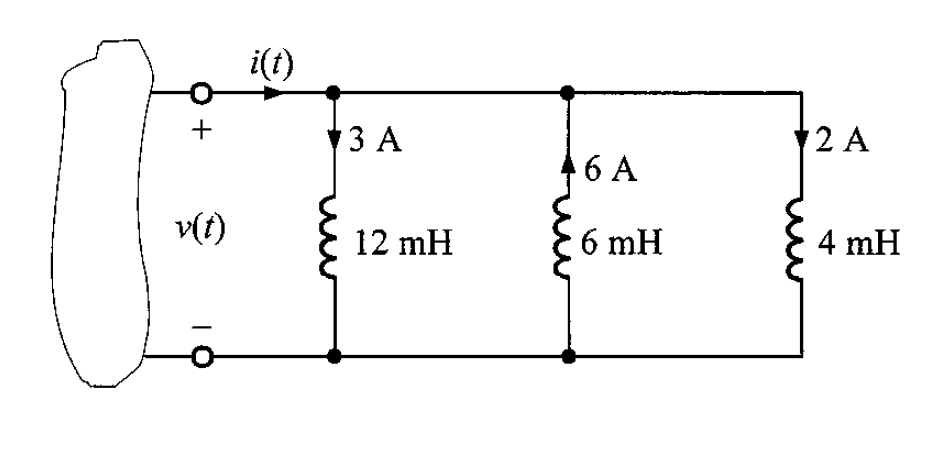
Solución. En el circuito se observa que todos los inductores están en paralelo, así que, se calcula la inductancia equivalente en paralelo.
Y calculando la corriente inicial total del circuito, resulta