Realimentación en circuitos amplificadores. Circuitos eléctricos.

Introducción

La ganancia de un amplificador puede ser controlada por la realimentación de una parte de su salida a su entrada como se hace con el amplificador ideal de la figura 1 a través de la resistencia $R_2$ . La relación de realimentación $R_1 / (R_1 + R_o)$ afecta a la ganancia total y hace al amplificador menos sensible a las variaciones de $k$ .

Figura 1. Modelo de un amplificador con realimentación.

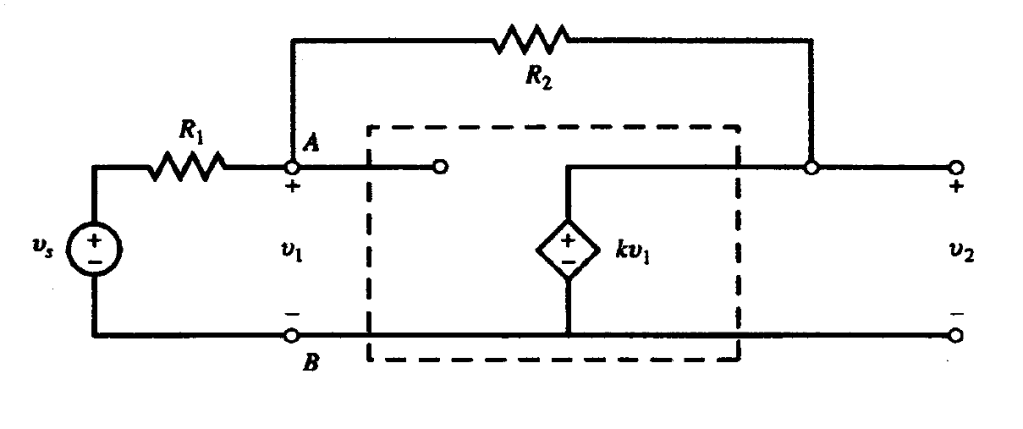
Para obtener la relación $v_2 / v_s$ , se empieza por utilizar la LKC en el nodo A.

$\displaystyle \frac{v_1 - v_s}{R_1} + \frac{v_1 - v_2}{R_2} = 0$

$\displaystyle \frac{v_1}{R_1} - \frac{v_s}{R_1} + \frac{v_1}{R_2} - \frac{v_2}{R_2} = 0$

$\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_2} \right) v_1 - \frac{v_2}{R_2} - \frac{v_s}{R_1} = 0$

Recordando que $v_2 = k v_1$ , al sustituirlo se tiene que

$\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_2} \right) v_1 - \frac{k v_1}{R_2} - \frac{v_s}{R_1} = 0$

$\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_2} - \frac{k}{R_2} \right) v_1- \frac{v_s}{R_1} = 0$

$\displaystyle \left(\frac{1}{R_1} + \frac{1-k}{R_2} \right) v_1 - \frac{v_s}{R_1} = 0$

$\displaystyle \left[\frac{R_2 + (1-k) R_1}{R_1 R_2} \right] v_1 - \frac{v_s}{R_1} = 0$

Despejando $v_1$

$\displaystyle \left[\frac{R_2 + (1-k) R_1}{R_1 R_2} \right] v_1 = \frac{v_s}{R_1}$

$\displaystyle v_1 = \frac{R_1 R_2 v_s}{R_1[R_2 + (1-k) R_1]}$

$\displaystyle v_1 = \left[ \frac{R_2}{R_2 + (1-k) R_1} \right] v_s$

Sustituyendo en la ecuación $v_2 = k v_1$ , finalmente se tiene que

$\displaystyle v_2 = k \left[\frac{R_2}{R_2 + (1-k) R_1} \right] v_s$

$\displaystyle \frac{v_2}{v_s} = \frac{k R_2}{R_2 + (1-k) R_1}$

Problema resuelto

Problema 1. En la figura 2, $R_1 = 1 \ \text{k} \Omega$ y $R_2 = 5 \ \text{k} \Omega$ .

a) Calcular $v_2 / v_s$ en función de la ganancia en lazo abierto.
b) Calcular $v_2 /v_s$ para $k=100$ y $k=1000$ .

Solución del a). Las figuras 1 y 2 difieren solamente en la polaridad de la fuente dependiente de voltaje. Para calcular $v_2 /v_s$ , nuevamente se utiliza LKC en el nodo A.

$\displaystyle \frac{v_1 - v_s}{R_1} + \frac{v_1 - v_2}{R_2} = 0$

$\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_2} \right) v_1 - \frac{v_2}{R_2} - \frac{v_s}{R_1} = 0$

Recordando que $v_2 = - k v_1$ , al sustituirlo se tiene que

$\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_2} \right) v_1 + \frac{k v_1}{R_2} - \frac{v_s}{R_1} = 0$

$\displaystyle \left(\frac{1}{R_1} + \frac{1}{R_2} + \frac{k}{R_2} \right) v_1- \frac{v_s}{R_1} = 0$

$\displaystyle \left(\frac{1}{R_1} + \frac{1+k}{R_2} \right) v_1 - \frac{v_s}{R_1} = 0$

$\displaystyle \left[\frac{R_2 + (1+k) R_1}{R_1 R_2} \right] v_1 - \frac{v_s}{R_1} = 0$

Despejando $v_1$

$\displaystyle v_1 = \left[ \frac{R_2}{R_2 + (1+k) R_1} \right] v_s$

Sustituyendo en la ecuación $v_2 = - k v_1$

$\displaystyle v_2 = - k \left[\frac{R_2}{R_2 + (1+k) R_1} \right] v_s$

$\displaystyle \frac{v_2}{v_s} = - \frac{k R_2}{R_2 + (1+k) R_1}$

Sustituyendo los valores dados por el problema, resulta

$\displaystyle \frac{v_2}{v_s} = - \frac{k (5 \ \text{k})}{5 \ \text{k} + (1+k) (1 \ \text{k})}$

$\displaystyle \frac{v_2}{v_s} = - \frac{5k \ \text{k}}{5 \ \text{k} + 1 \ \text{k} + k \ \text{k}}$

$\displaystyle \frac{v_2}{v_s} = - \frac{5k \ \text{k}}{6 \ \text{k} + k \ \text{k}}$

Por lo tanto, la relación esperada es

$\displaystyle \therefore \frac{v_2}{v_s} = - \frac{5k}{6 + k}$

Solución del b). Cuando $k=100$ , la relación $v_2 /v_s$ es

$\displaystyle \frac{v_2}{v_s} = - \frac{5k}{6 + k}$

$\displaystyle \frac{v_2}{v_s} = - \frac{5(100)}{6 + 100}$

$\displaystyle \frac{v_2}{v_s} = - \frac{500}{106}$

$\displaystyle \therefore \frac{v_2}{v_s} = -4.72$

Y cuando $k=1000$ , la relación $v_2 /v_s$ es

$\displaystyle \frac{v_2}{v_s} = - \frac{5k}{6 + k}$

$\displaystyle \frac{v_2}{v_s} = - \frac{5(1000)}{6 + 1000}$

$\displaystyle \frac{v_2}{v_s} = - \frac{5000}{1006}$

$\displaystyle \therefore \frac{v_2}{v_s} = -4.97$

Al comparar los resultados obtenidos del inciso b, se observa que hubo un aumento de diez veces en el valor de $k$ , lo cual provocó únicamente un 5.3 por 100 de cambio en $v_2 / v_s$ , ya que

$\displaystyle \frac{4.97 - 4.72}{4.72} \times 100 = 5.3$ %

Además, para valores mayores de $k$ la relación $v_2 / v_s$ se aproxima a $- R_2/R_1$ , que es independiente de $k$ .

Realimentación en circuitos amplificadores. Circuitos eléctricos.

Introducción

Problema resuelto

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Realimentación en circuitos amplificadores. Circuitos eléctricos.

Introducción

Problema resuelto

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta