Amplificador operacional. Circuitos eléctricos.

Introducción

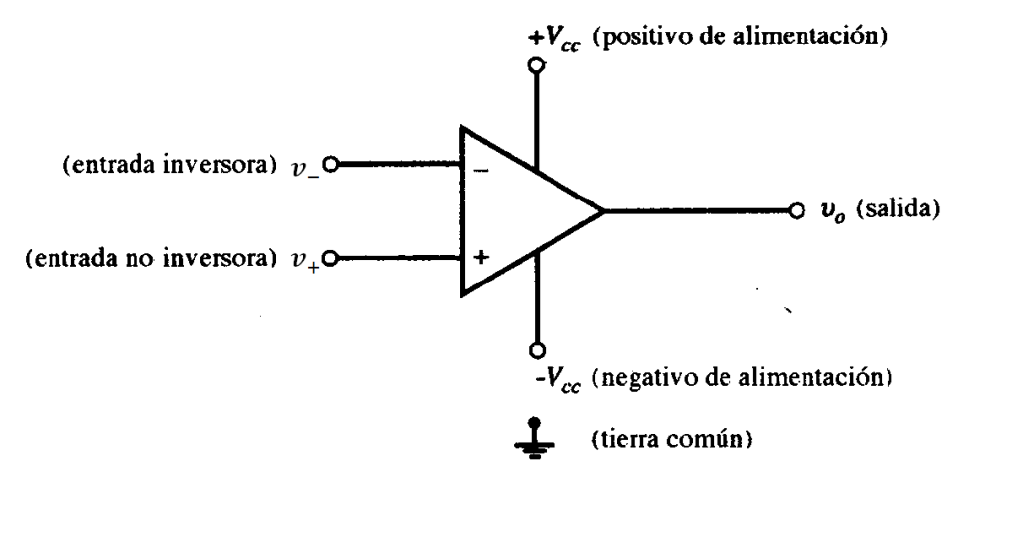
El amplificador operacional (amp. op.) es un dispositivo con dos terminales de entrada denominados entrada inversora (-) y entrada no inversora (+). El dispositivo se conecta además a una fuente de corriente continua ( y ). La referencia común para la entrada, la salida y la fuente de alimentación está fuera del amplificador operacional y se denomina tierra (figura 1).

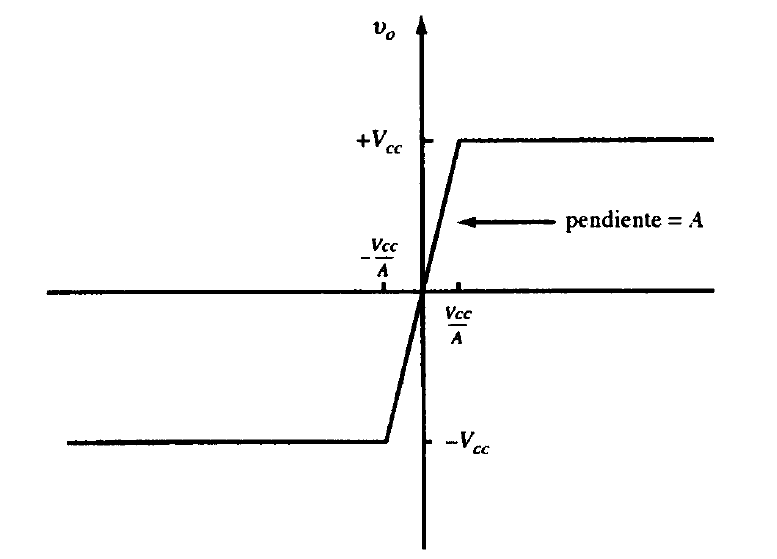
El voltaje de salida depende de . Despreciando los efectos capacitivos, la función de transferencia es la indicada en la figura 2. En la zona lineal latex A$ en circuito abierto es generalmente muy alta. El valor de se satura cuando la entrada está por encima de la zona lineal.

En la figura 3 se representa un modelo de un amplificador operacional en la zona lineal, en donde se han omitido las conexiones de la fuente de alimentación por su simplicidad. En la práctica, es grande y es pequeña, y es del orden de a algunos millones. El modelo de la figura 3 es válido cuando el voltaje de salida se encuentre dentro del intervalo y . es generalmente de 5 a 18 V.

Problema resuelto

Problema 1. En la figura 4 se tiene un amplificador operacional donde , , y . Obtener . Suponer que el amplificador no está saturado.

Solución. Para resolver esto, primero se obtendrá la expresión por medio del nodo B y utilizando las LKC. Entonces, se observa que y . Luego

Despejando resulta

Sustituyendo en la ecuación , se tiene lo siguiente

Desarrollando la relación , resulta

Con los valores de cada resistor y el de la ganancia, el resultado final es

---