Introducción
En un circuito resistencia-inductor-capacitor (R-L-C) de corriente alterna en serie se unen de esta forma una o varias resistencias (R), con uno o varios inductores (L), junto con uno o varios capacitores (C), todos conectados a un dispositivo que les suministra corriente alterna. Debido a que tanto el inductor como el capacitor se oponen siempre al flujo de la corriente, el ángulo de fase () de los circuitos (R-L-C) de corriente alterna en serie es negativo cuando
(reactancia capacitiva sea mayor que la reactancia inductiva), por lo que la corriente estará adelantada respecto a la tensión, positivo cuando
.

Figura 1. Esquema general de un circuito RLC de corriente alterna. 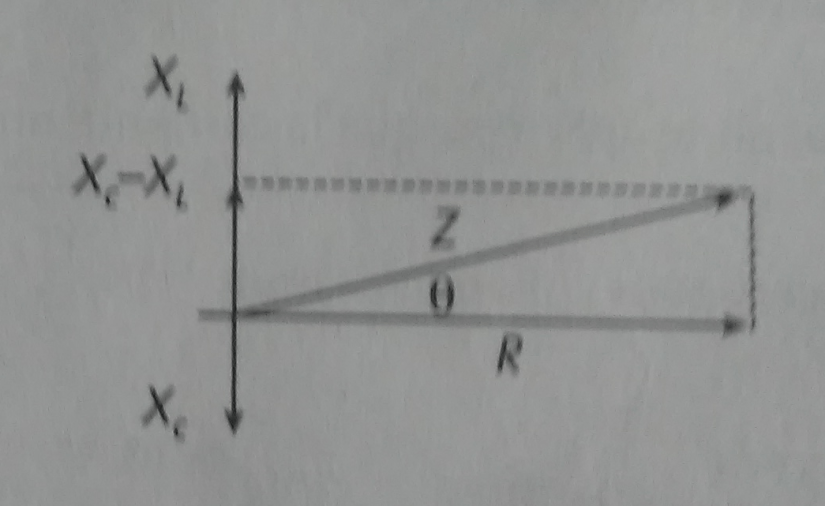
Figura 2. Relación entre vectores de un circuito RLC de corriente alterna.
En el caso de que un circuito resistencia-inductor-capacitor de corriente alterna en serie de una radio que sea alimentado con una amplia gama de frecuencias, se puede ajustar o sincronizar el inductor y el capacitor para permitir el paso de sólo una en particular.
Al conectar varias resistencias, varios inductores y varios capacitores en serie, primero se tiene que calcular la resistencia total, la reactancia inductiva total y la reactancia capacitiva total. Luego se sustituyen en las ecuaciones correspondientes.
Ecuaciones de un circuito RLC en corriente alterna
Las ecuaciones que describen al circuito resistencia-inductor-capacitor de corriente alterna en serie se muestran a continuación.
Donde:
es la impedancia, en Ohms (
).
es la resistencia, en Ohms (
).
-
es la reactancia inductiva, en Ohms (
).
es la reactancia capacitiva, en Ohms (
).
Donde:
es la intensidad de corriente perteneciente a la impedancia, en Amperes (A).
es la tensión de corriente perteneciente a la impedancia, en volts (V).
es la impendiancia, en Ohms (
).
Donde:
es la intensidad de corriente perteneciente a la resistencia, en Amperes (A).
es la tensión de corriente perteneciente a la resistencia, en volts (V).
es la resistencia, en Ohms (
).
Donde:
es la intensidad de corriente perteneciente a la reactancia inductiva, en Amperes (A).
es la tensión de corriente perteneciente a la reactancia inductiva, en volts (V).
es la reactancia inductiva, en Ohms (
).
Donde:
es la intensidad de corriente perteneciente a la reactancia capacitiva, en Amperes (A).
es la tensión de corriente perteneciente a la reactancia capacitiva, en volts (V).
es la reactancia capacitiva, en Ohms (
).
Donde:
es la tensión de corriente perteneciente a la impedancia, en volts (V).
es la tensión de corriente pertenenciente a la resistencia, en volts (V).
-
es la tensión de corriente pertenenciente a la reactancia inductiva, en volts (V).
es la tensión de corriente pertenenciente a la reactancia capacitiva, en volts (V).
Donde:
es la reactancia inductiva, en Ohms (
).
es la frenciencia, en Hertz (Hz).
es la inductancia, en Henry (H).
Donde:
es la reactancia capacitiva, en Ohms (
).
es la frenciencia, en Hertz (Hz).
es la capacitancia, en Farad (F).
Donde:
es el ángulo de fase, en grados (°).
es la reactancia inductiva, en Ohms (
).
es la reactancia capacitiva, en Ohms (
).
es la resistencia, en Ohms (
).
Problema resuelto
Problema. Se conecta una resistencia de 50 (), un inductor de 0.5 Henry y un capacitor de 15 (
F), todos en serie, a una fuente de ca de 120 (V) y 60 (Hz). Para este circuito eléctrico, calcular:
- a) La corriente que circula.
- b) El ángulo de fase.
Solución. Calculo de la reactancia capacitiva
Cálculo de la reactancia inductiva
Cálculo de la impedancia
Solución del a). Cálculo de la intensidad de la corriente
Solución del b). Cálculo del ángulo de fase