Introducción
Un intervalo es un conjunto definido de valores que tienen orden; está acotado por un ínfimo y un supremo a los cuales se les denomina puntos extremos y
del intervalo. Los puntos extremos de un intervalo cerrado están incluidos en él , en tanto que los puntos extremos de un intervalo abierto no están incluidos en él. Algunos autores denotan los puntos extremos de un intervalo abierto con puntos «huecos» y los extremos de un intervalo cerrado con puntos «rellenos». Existen tres maneras de representar intervalos:
- Notación de intervalos.
- Desigualdades.
- Gráficamente.
| Tipo de intervalo | Notación | Desigualdad | Grafica |
| Cerrado | 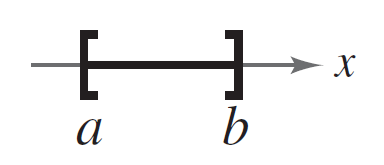 | ||
| Abierto |  | ||
| Mixto | 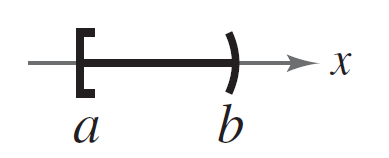 | ||
| Mixto | 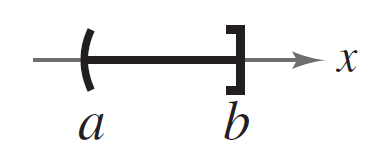 |
Los símbolos , infinito positivo, y
, infinito negativo, no representan números reales. Simplemente son símbolos prácticos que se utilizan para describir lo ilimitado de un intervalo. Por ejemplo
o
.
| Tipo de intervalo | Notación | Desigualdad | Grafica |
| Infinito |  | ||
| Infinito |  | ||
| Infinito | 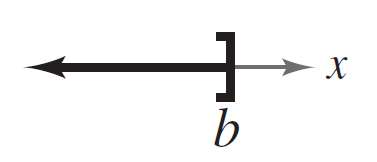 | ||
| Infinito |  | ||
| Toda la recta real |
En matemáticas o en la vida real un intervalo representa el conjunto de todas las posibles soluciones que puede tener una ecuación, una desigualdad o un problema.
Problemas resueltos
¿Como representar un intervalos en una desigualdad?
Problema 1. Usar la notación de desigualdades para describir cada uno de lo siguiente.
- a)
es como máximo 2.
- b)
es al menos
.
- c) Toda
en el intervalo
Solución.
- a) El enunciado «
es a lo más 2″ puede representarse con
.
- b) El enunciado «
es al menos -3$ puede representarse con
.
- c) El enunciado «Toda
en el intervalo
» puede representarse con
.
¿Cómo interpretar un intervalo?
Problema 2. Dar una descripción verbal de cada uno de los siguientes intervalos
- a)
- b)
- c)
Solución.
- a) Este intervalo está formado por todos los números reales que sean mayores a
y menores que 0.
- b) Este intervalo está formado por todos los números reales que sean mayores o iguales a 2.
- c) Este intervalo está formado por todos los números reales negativos.
Operaciones con intervalos
Problema 3. Determinar el conjunto de números reales definido por
- a)
- b)
Solución.
- a) La manera de determinar su conjunto es
- b) Y para este caso