Introducción
Las desigualdades lineales están mezcladas con las funciones parte por parte y usarse para describir comúnmente cada intervalo de la función.
De la misma manera que las ecuaciones lineales tienen sólo una solución, las desigualdades lineales sólo pueden tener un intervalo de soluciones. Su intervalo solución estará determinado por la posición de la línea recta dada por la desigualdad y el eje de las abscisas (eje ). A continuación se muestran unas gráficas en donde se observa los cuatro posibles casos de los intervalos solución y sus respectivas desigualdades.

Figura 1. Representación gráfica cuando x es mayor a 0. 
Figura 2. Representación gráfica cuando -x es mayor a 0. 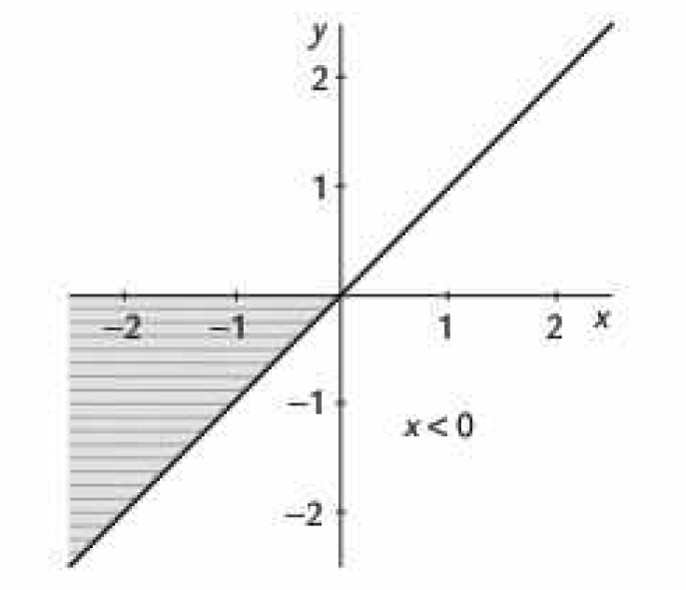
Figura 3. Representación gráfica cuando x es menor a 0 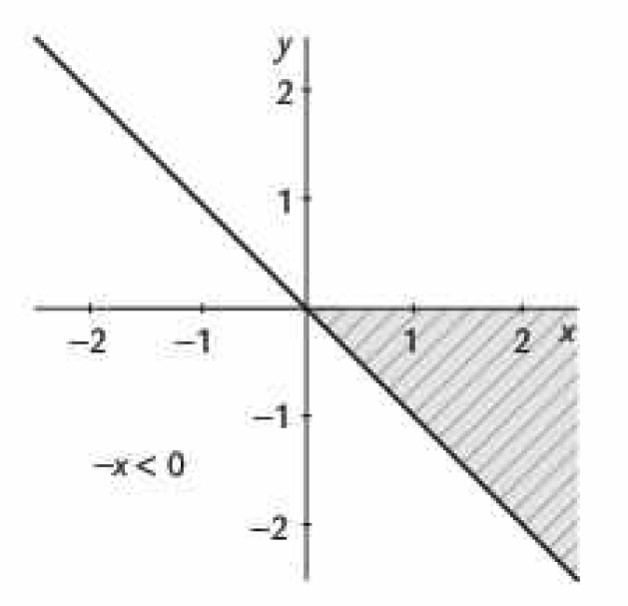
Figura 4. Representación gráfica cuando -x es menor a 0
Nota
Los símbolos y
se conocen como símbolos de desigualdad estricta y se leen «menor que» y «mayor que» respectivamente.
Los símbolos y
se conocen como símbolos de desigualdad no estricta y se leen «menor o igual que» y «mayor o igual que» respectivamente.
- La expresión
abrevia los casos
o
.
- La expresión
abrevia los casos
o
.
Problemas resueltos
Problema 1. Resolver la desigualdad .
Solución. Esta desigualdad solicita todos aquellos valores de que hagan que la línea recta
esté por encima del eje
, de tal manera que
sea igual o mayor que cero. Así que
En conclusión, se tiene un intervalo , la cual, la línea recta estará por encima del eje
y la desigualdad tomará valores iguales o mayores que cero. Para terminar, se visualiza una representación gráfica referente a la solución de la desigualda.

Problema 2. Resolver la siguiente desigualdad: .
Solución. Para resolver esto, los términos con que acompañan variable estarán en el primer miembro (lado izquierdo o antes del símbolo de la desigualdad) y los términos restantes se colocarán en el segundo miembro (lado derecho o después del símbolo de la desigualdad).
Por último, se despeja
Nota: Si el coeficiente que acompaña a la variable tiene un signo negativo, al momento de despejarlo, el símbolo de la desigualdad cambia o se invierte.
Se concluye que los valores de que solucionan la desigualdad son los que están en
. Por último, se representa está solución gráficamente (figura 6).

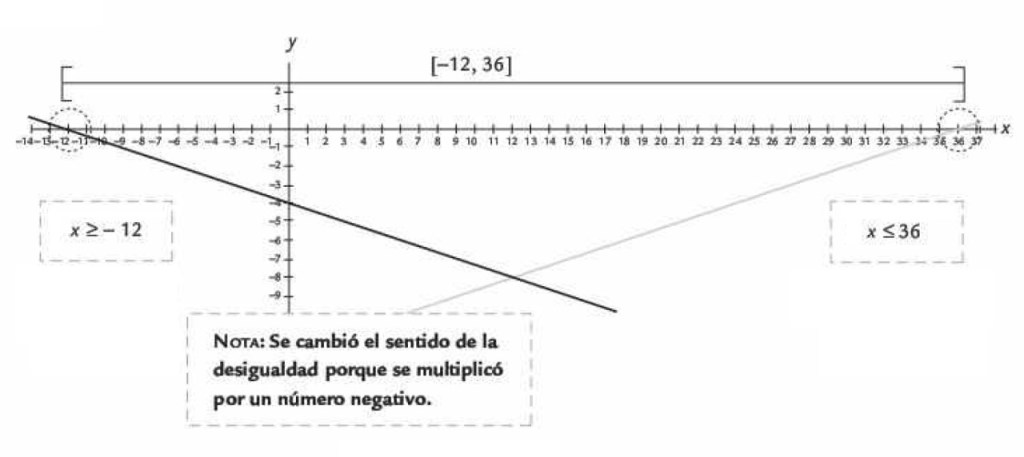
Problema 3. Resolver la desigualda .
Solución. Para este caso se debe resolver en ambos lados o miembros de la desigualdad.
Se concluye que el intervalo encontrado es .
Para representarlo gráficamente, se utilizan estos pasos:
1. Se forman dos desigualdades de derecha a izquierda, ambas divididas por sus respectivos signos.
2. Se despejarán ambas desigualdades de modo que del lado izquierdo de la desigualdad queden los términos que acompañen a la variable y del lado derecho queden los términos constantes.
3. Por último, se solucionará y se despejará cada desigualdad por separado.
Graficando esto, se tiene lo siguiente