Introducción
Resolver una desigualdad significa determinar el conjunto de números reales que la satisfacen. Una desigualdad o inecuación tiene infinitas soluciones en forma de intervalo o unión de intervalos de números reales.
Para resolver una desigualdad se utilizan los axiomas de los números reales y el álgebra que de ellos se desarrolla.
Problemas resueltos.
Problema 1. Resolver la desigualdad .
Solución. Primero se debe observar que todos los términos diferentes de cero estén ubicados en el lado izquierdo y el cero en el lado derecho. Después, se factoriza la desigualdad cuadrática (lado izquierdo).
La parte izquierda de la desigualdad se considera como el producto de dos factores, y este producto es positivo, lo cual ocurre cuando los factores son del mismo signo.
Para ello se tienen los siguientes casos:
Caso 1. Si , entonces
Analizando gráficamente estos resultados
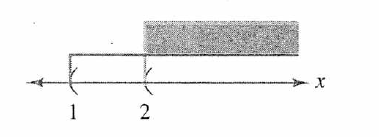
El conjunto solución de estas dos desigualdades es .
Caso 2. Si , entonces
Analizando gráficamente estos resultados

El conjunto solución de estas dos desigualdades es .
Finalmente, la solución de la desigualdad se obtiene al unir las soluciones obtenidas en los casos 1 y 2. Es decir la solución es el conjunto . Esto se puede representar gráficamente a continuación (figura 3).

Problema 2. Resolver la desigualdad .
Solución. Se deben colocar todos los términos diferentes en el lado izquierdo y el cero en el lado derecho.
Después, se factoriza la representación cuadrática (lado izquierdo)
Considerando la parte izquierda de la desigualdad como el producto de dos factores, este producto será menor o igual a cero, lo cual ocurre cuando los factores son de signos diferentes o cero. Para esta situación, se desarrollarán dos casos, el primero término tendrá la misma posición de signo de la desigualdad y el segundo término estará con signo invertido.
Caso 1. Si , entonces
El conjunto solución de estas dos desigualdades es .
Representando esto gráficamente, se tiene lo siguiente (figura 4).

Caso 2. Si , entonces
El conjunto solución de estas dos desigualdades es
Representándolo gráficamente, se observa que

Finalmente, la solución de la desigualda se obtiene la unir las soluciones obtenidas en los casos 1 y 2. Basándose en la figura 4, la solución es el conjunto .