Introducción
El dominio es el conjunto de valores que puede tomar la variable independiente mientras que el rango (o también llamado imagen) es el conjunto de valores que puede tomar la variable dependiente
, una vez, asignados los valores a la variable independiente.
¿Cómo encontrar el dominio y el rango de cualquier función?
- Identificar el nombre o tipo de función.
- Reconocer las restricciones algebraicas de la función.
- Si existen raíces pares, el contenido del radicando debe ser mayor que o igual a cero.
- Si existen divisiones, el denominador debe ser diferente de cero.
- Los logaritmos deben ser mayores a cero.
- Si es una función compuesta, analizar sus componentes individuales y combinar los posibles dominios.
- Si la función representa un modelo matemático, incluye las limitaciones físicas del problema.
- Una vez determinado el dominio, se procede a obtener el rango.
- El rango o la imagen de una función está dada por el valor mayor y el valor menor del dominio, excepto para aquellos en los cuales del dominio es simétrico; para tales casos se puede usar el valor menor o mayor y la mitad del dominio.
Problemas resueltos
Problema 1. Determinar el dominio para las siguientes funciones
Solución. Como debe ser real, al hacer mayor que o igual que se tiene que
Entonces, el intervalo solución sería o mejor dicho
. Por tanto, el dominio de
es
.
Solución. Como debe ser real, la expresión dentro de la raíz cuadrada puede ser igual o mayor a cero.
Con esto, se tienen dos valores de . Por tanto, el intervalo solución es
. Por lo que el dominio de
es
.
Solución. Igualando a cero el denominador
Entonces, la función está definida para todo excepto
. Por tanto, el dominio de
es
o mejor dicho
.
Solución. Igualando a cero la ecuación del denominador
Como la función está definida para , el dominio para
es
. Esto también se puede expresar como una notación de construcción de conjuntos, por lo que sería
.
Solución. Como para todo
, el dominio de
es
, es decir, es el conjunto de todos los números reales.
Problema 2. Hallar los dominios y rangos para las siguientes funciones.
Solución. El dominio de es
o también
si se expresa en notación de intervalos mientras que el rango de
es
.
Solución. Para este caso no son dos funciones, sino una sola función que presenta una regla de correspondencia en dos partes, en donde el dominio para la primera parte es mientras que la segunda es
; el dominio de
es la unión de los intervalos
que esto es equivalente a
. Para el rango de
estaría conformado por
o
.
el mayor entero menor o igual que
.
Solución. El dominio de es es
(números reales) y el rango es
(números enteros).
Solución. El dominio de es
o mejor dicho
y el rango de
es
.
Solución. El dominio de es
(todos los números) y el rango de
es
.
Solución. El dominio de es
y el rango de
es
.
Solución. El dominio de es
y el rango de
es
.
Solución. El dominio de es
(todos los números) y el rango de
es
.
Solución. El dominio de la primera expresión es mientras que la segunda es
. Por tanto, el dominio de
es
o mejor dicho,
. Para el rango de
, la primera expresión sería
mientras que su segunda es
, por lo que al unir ambos resultados, el final esperado es
.
Problema 3. Dibujar el gráfico de la función definida por:
Y determinar el dominio y el recorrido de la función dada.
Solución. El gráfico es el siguiente

El dominio son todos los números reales positivos y el recorrido es el conjunto de enteros, 5, 10, 15, 20, …
Problema 4. Expresar la longitud de una cuerda de un círculo de radio 8 como función de su distancia
(en pulgadas) al centro del círculo. Determinar el dominio de la función.
Solución. Se realiza el siguiente gráfico
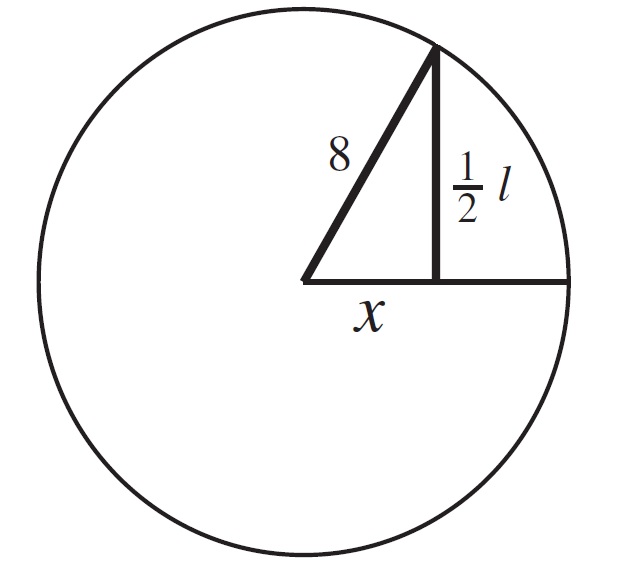
Se observa que (Por el teorema de pitágoras), luego
Se concluye que el dominio es el intervalo o también
.