Representación e identificación de funciones. Cálculo diferencial.

Notación de funciones

La notación de funciones permite distinguir la variable dependiente de la independiente, y se expresa de la siguiente manera:

donde representa el nombre de la función (puede ser cualquier letra, como por ejemplo ); luego se escribe entre paréntesis la letra de la variable independiente , y después del signo de la igualdad (=) se escribe el resto del modelo matemático.

Evaluación de funciones

Evaluar una función significa encontrar el valor real que le corresponde a la variable dependiente, una vez asignado un valor a la variable independiente.

Como ejemplo, se tiene la siguiente la función . Cuando , el valor de la función sería

Existen tres maneras de representar e identificar las funciones: analítica, tabular y gráficamente. Cada uno expresa la manera con se pueda visualizar los problemas reales utilizando símbolos, datos ordenadas o gráficos, con el fin de comprender y analizar el problema.

Representación analítica

Representa el lenguaje matemático puro a través de símbolos y números que se expresa mediante una fórmula matemática. Por ejemplo: .

Analíticamente no representa una función de si al momento de despejar ésta tiene exponente par. Por ejemplo: .

Representación tabular

Esto se hace a través de un conjunto de pares ordenados .

x	-5	-4	-3	-2	-1	0	1	2	3	4	5
y	25	16	9	4	1	0	1	4	9	16	25

Tabularmente no representa una función de si existen dos pares ordenados con diferente valor de para el mismo valor de . Ejemplo: y .

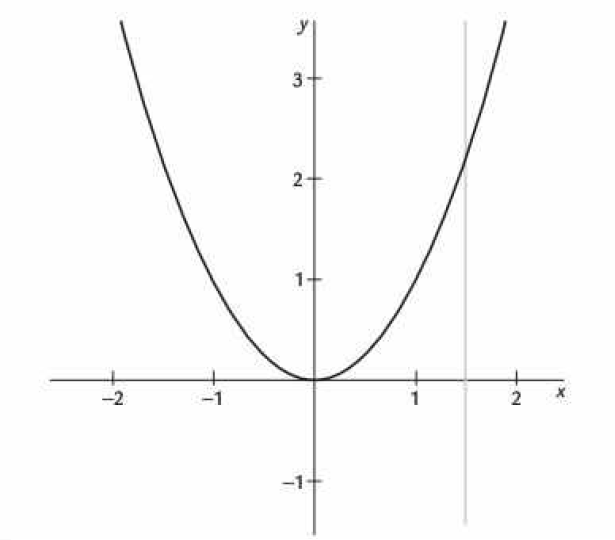
Representación gráfica

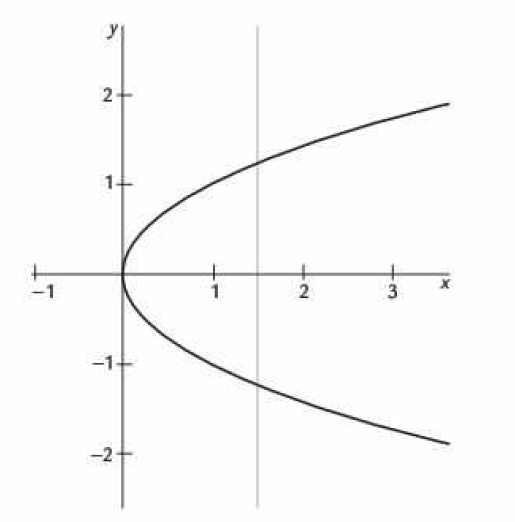
Esto es a través del dibujo de pares ordenados en el plano cartesiano o cualquier otro sistema de coordenadas. Gráficamente no representa una función de si en la gráfica ésta es cruzada dos o más veces por una línea vertical.

---