Introducción
Si es una curva suave dada por
en un intervalo
, entonces la longitud de arco
en el intervalo es
Problemas resueltos
Problema 1. Encuentre la longitud de arco de la curva dada por desde
hasta
, como se muestra en la siguiente figura.
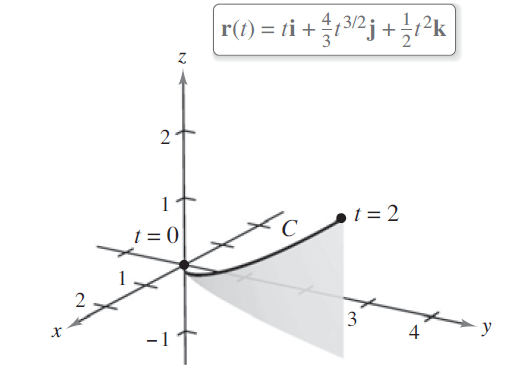
Solución. De la función del problema, se determina su primera derivada
Después, se determina su magnitud
Tomando la fórmula de la longitud de arco y sustituyendo
Problema 2. Hallar la longitud de un giro de la hélice dada por .
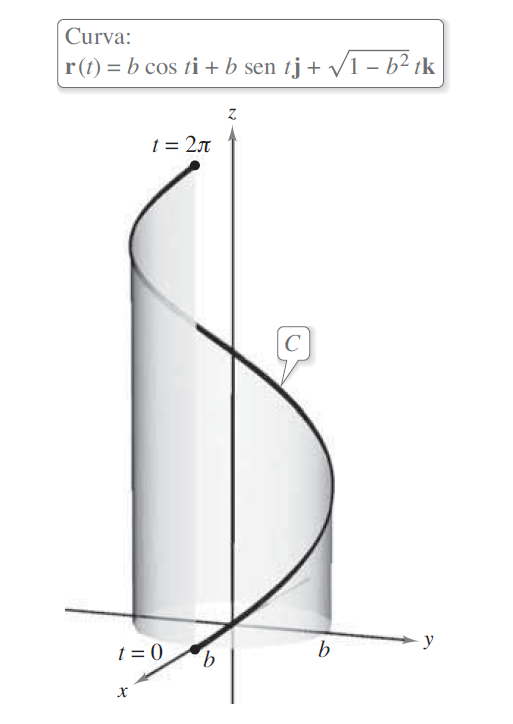
Solución. Se determina la primera derivada de la función dada
Después, se calcula su magnitud
Realizando la sustitución en la fórmula de la longitud de arco, resulta
Se concluye que la longitud de un giro de la hélice es de .