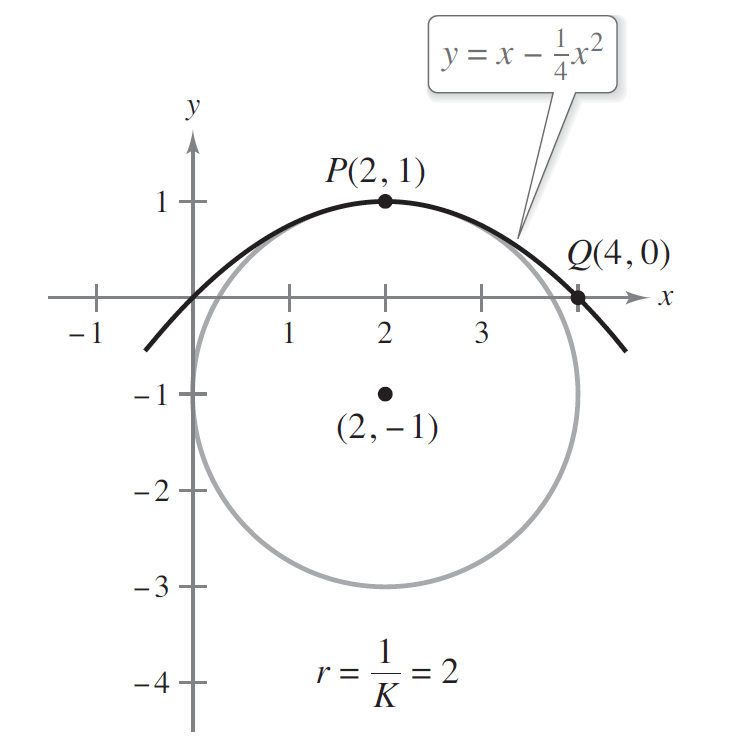Curvatura. Calculo vectorial.

Introducción

Sea $C$ una curva suave (en el plano o en el espacio) dada por $\mathbf{r} (s)$ , donde $s$ es el parámetro longitud de arco. La curvatura $K$ en $s$ está dada por

$\displaystyle K = \left| \left| \frac{d\mathbf{T}}{ds} \right| \right| = || \mathbf{T}'(s)||$

Figura 1. Representación de la curvatura.

Figura 2. La magnitud de la razón de cambio de $\mathbf{T}$ respecto a la longitud de arco es la curvatura de una curva.

Teorema 1. Si $C$ es una curva suave dada por $\mathbf{r} (t)$ , entonces la curvatura $K$ de $C$ en $t$ está dada por

$\displaystyle K = \frac{||\mathbf{T}'(t)||}{||\mathbf{r}'(t)||} = \frac{||\mathbf{r}'(t) \times \mathbf{r}'' (t)||}{||\mathbf{r}'(t)||^3}$

Demostración. Como $\displaystyle ||\mathbf{r}'(t)|| = \frac{ds}{dt}$ , la fórmula anterior implica que la curvatura es el cociente de la razón de cambio del vector tangente $\mathbf{T}$ entre la razón de cambio de la longitud de arco. Para comprenderlo, sea $\Delta t$ un número pequeño. Después

$\displaystyle \frac{\mathbf{T}'(t)}{ds/dt} \approx \frac{[\mathbf{T}(t + \Delta t) - \mathbf{T} (t)]/\Delta t}{[s(t + \Delta t) - s(t)]/\Delta t} = \frac{\mathbf{T}(t + \Delta t) - \mathbf{T} (t)}{s(t + \Delta t) - s(t)} = \frac{\Delta \mathbf{T}}{\Delta s}$

Es decir, para un $\Delta s$ dado, cuanto mayor sea la longitud $\Delta \mathbf{T}$ de la curva se dobla más en $t$ (figura 4).

Teorema 2. Si $C$ es una curva suave dada por $\mathbf{r} (t)$ , entonces la curvatura $K$ de $C$ en $t$ está dada por

$\displaystyle K = \frac{|| \mathbf{T}' (t)||}{||\mathbf{r}' (t)||} = \frac{|| \mathbf{r}'(t) \times \mathbf{r}''(t)||}{||{\mathbf{r} (t)||}^3}$

Teorema 3: Curvatura en coordenadas polares. Si $C$ es la gráfica de una función dos veces derivable, entonces la curvatura en el punto está dada por $y=f(x)$ , y la curvatura $K$ en el punto $(x,y)$ es

$\displaystyle K = \frac{|f''(x)|}{\left\{1 + {[f'(x)]}^2\right\}^{3/2}} = \frac{|y''|}{{[1 + {(y')}^2]}^{3/2}}$

Problemas resueltos

Problema 1. Demostrar que la curvatura de un círculo de radio $r$ es $\displaystyle K = \frac{1}{r}$ .

Solución. Se considera un circulo que está centrado en el origen. Sea $(x,y)$ cualquier punto en el círculo y sea $s$ la longitud de arco desde $(r,0)$ hasta $(x,y)$ . $\theta$ representará el ángulo central del circulo, por lo que la función vectorial del círculo es

$\displaystyle r(\theta) = r \cos{\theta} \mathbf{i} + r \sin{\theta} \mathbf{j}$

Recordando la formula de la longitud de un arco circular ( $s = r \theta$ , que al despejar sería $\displaystyle \theta = \frac{s}{r}$ ), la función vectorial se puede reescribir (en términos del parámetro longitud de arco) de la siguiente manera

$\displaystyle r(s) = r \cos{\frac{s}{r}} \mathbf{i} + r \sin{\frac{s}{r}} \mathbf{j}$

Figura 6. Representación gráfica del problema 1.

Determinando su primera derivada resulta que

$\displaystyle \frac{d}{ds} [r(s)] = r \frac{d}{ds} \left[\cos{\frac{s}{r}} \right] \mathbf{i} + r \frac{d}{ds} \left[\sin{\frac{s}{r}} \right] \mathbf{j}$

$\displaystyle r'(s) = r \cdot \frac{1}{r} \left(-\sin{\frac{s}{r}} \right) \mathbf{i} + r \cdot \frac{1}{r} \left(\cos{\frac{s}{r}} \right) \mathbf{j}$

$\displaystyle r'(s) = -\sin{\frac{s}{r}} \mathbf{i} + \cos{\frac{s}{r}} \mathbf{j}$

Calculando la magnitud de este último resultado, se tiene que

$\displaystyle ||r'(s)|| = \left| \left|-\sin{\frac{s}{r}} \mathbf{i} + \cos{\frac{s}{r}} \mathbf{j} \right| \right|$

$\displaystyle ||r'(s)|| = \sqrt{{\left(-\sin{\frac{s}{r}} \right)}^2 + {\left(\cos{\frac{s}{r}} \right)}^2}$

$\displaystyle ||r'(s)|| = \sqrt{\sin^2{\frac{s}{r}} + \cos^2{\frac{s}{r}}} = \sqrt{1}$

$\displaystyle ||r'(s)|| = 1$

Luego, es necesario calcular el vector unitario tangente,

$\displaystyle \mathbf{T} (s) = \frac{\mathbf{r}'(s)}{||\mathbf{r}'(s)||}$

$\displaystyle \mathbf{T} (s) = \frac{-\sin{\frac{s}{r}} \mathbf{i} + \cos{\frac{s}{r}} \mathbf{j}}{1}$

$\displaystyle \mathbf{T} (s) = -\sin{\frac{s}{r}} \mathbf{i} + \cos{\frac{s}{r}} \mathbf{j}$

Y por último la derivada del vector unitario tangente

$\displaystyle \frac{d}{ds} [\mathbf{T} (s)] = \frac{d}{ds} \left[-\sin{\frac{s}{r}} \right] \mathbf{i} + \frac{d}{ds} \left[\cos{\frac{s}{r}} \right] \mathbf{j}$

$\displaystyle \mathbf{T}' (s) = - \frac{1}{r} \cos{\frac{s}{r}} \mathbf{i} - \frac{1}{r} \sin{\frac{s}{r}} \mathbf{j}$

Finalmente, la curvatura es

$\displaystyle K = || \mathbf{T}'(s)||$

$\displaystyle K = \left| \left| - \frac{1}{r} \cos{\frac{s}{r}} \mathbf{i} - \frac{1}{r} \sin{\frac{s}{r}} \mathbf{j} \right| \right|$

$\displaystyle K = \sqrt{ {\left(- \frac{1}{r} \cos{\frac{s}{r}} \right)}^2 + {\left(- \frac{1}{r} \sin{\frac{s}{r}} \right)}^2 }$

$\displaystyle K = \sqrt{ \frac{1}{r^2} \cos^2{\frac{s}{r}} + \frac{1}{r^2} \sin^2{\frac{s}{r}} }$

$\displaystyle K = \sqrt{ \frac{1}{r^2} \left(\cos^2{\frac{s}{r}} + \sin^2{\frac{s}{r}} \right) }$

$\displaystyle K = \sqrt{ \frac{1}{r^2} \left(1 \right) } = \sqrt{ \frac{1}{r^2}}$

$\displaystyle \therefore K = \frac{1}{r}$

El círculo que pasa por el punto $P$ de radio $r = \frac{1}{K}$ se denomina círculo de curvatura si su centro se encuentra en el lado cóncavo de la curva y tiene en común con la curva una recta tangente en el punto $P$ . Al radio se le llama radio de curvatura en $P$ , y al centro se le llama centro de curvatura.

Problema 2. Determinar la curvatura de la curva definida por $\displaystyle \mathbf{r} (t) = 2t \mathbf{i} + t^2 \mathbf{j} - \frac{1}{3} t^3 \mathbf{k}$ .

Solución. Al no poder observarlo a simple vista si este parámetro represente la longitud de arco, se tomará la siguiente fórmula

$\displaystyle K = \frac{|| \mathbf{T}'(t) ||}{|| \mathbf{r}'(t) ||}$

donde está solicitando la magnitud de la primera derivada del vector tangente y la magnitud de la primera derivada del vector posición. Entonces, del vetor posición

$\displaystyle \mathbf{r} (t) = 2t \mathbf{i} + t^2 \mathbf{j} - \frac{1}{3} t^3 \mathbf{k}$

$\displaystyle \mathbf{r}' (t) = \frac{d}{dt} (2t) \mathbf{i} + \frac{d}{dt} (t^2) \mathbf{j} - \frac{d}{dt} \left(\frac{1}{3} t^3 \right) \mathbf{k}$

$\displaystyle \mathbf{r}' (t) = 2 \mathbf{i} + 2t \mathbf{j} - t^2 \mathbf{k}$

$\displaystyle ||\mathbf{r}' (t)|| = ||2 \mathbf{i} + 2t \mathbf{j} - t^2 \mathbf{k}||$

$\displaystyle ||\mathbf{r}' (t)|| = \sqrt{{(2)}^2 + {(2t)}^2+ {(-t^2)}^2}$

$\displaystyle ||\mathbf{r}' (t)|| = \sqrt{4 + 4t^2+ t^4} = \sqrt{{(t^2 + 2)}^2}$

$\displaystyle ||\mathbf{r}' (t)|| = t^2 + 2$

Para el vector tangente, se tiene que

$\displaystyle \mathbf{T} (t) = \frac{\mathbf{r}'(t)}{|| \mathbf{r}' (t) ||}$

$\displaystyle \mathbf{T} (t) = \frac{2 \mathbf{i} + 2t \mathbf{j} - t^2 \mathbf{k}}{t^2 + 2}$

Calculando la primera derivada del vector tangente

$\displaystyle \mathbf{T}' (t) = \frac{d}{dt} \left(\frac{2 \mathbf{i} + 2t \mathbf{j} - t^2 \mathbf{k}}{t^2 + 2} \right)$

$\displaystyle \mathbf{T}' (t) = \frac{(t^2 + 2)(2 \mathbf{j} - 2t \mathbf{k}) - (2 \mathbf{i} + 2t \mathbf{j} - t^2 \mathbf{k})(2t)}{{(t^2 + 2)}^2}$

$\displaystyle \mathbf{T}' (t) = \frac{(2t^2 \mathbf{j} - 2t^3 \mathbf{k} + 4 \mathbf{j} - 4t\mathbf{k}) - (4t \mathbf{i} + 4t^2 \mathbf{j} - 2t^3 \mathbf{k})}{{(t^2 + 2)}^2}$

$\displaystyle \mathbf{T}' (t) = \frac{2t^2 \mathbf{j} - 2t^3 \mathbf{k} + 4 \mathbf{j} - 4t\mathbf{k} - 4t \mathbf{i} - 4t^2 \mathbf{j} + 2t^3 \mathbf{k}}{{(t^2 + 2)}^2}$

$\displaystyle \mathbf{T}' (t) = \frac{- 4t \mathbf{i} + (- 2t^2 + 4) \mathbf{j} - 4t\mathbf{k}}{{(t^2 + 2)}^2}$

Y su magnitud es

$\displaystyle ||\mathbf{T}' (t)|| = ||\frac{- 4t \mathbf{i} + (- 2t^2 + 4) \mathbf{j} - 4t\mathbf{k}}{{(t^2 + 2)}^2}||$

$\displaystyle ||\mathbf{T}' (t)|| = \frac{1}{{(t^2 + 2)}^2} \sqrt{{(- 4t)}^2 + {(- 2t^2 + 4)}^2 + {(-4t)}^2}$

$\displaystyle ||\mathbf{T}' (t)|| = \frac{1}{{(t^2 + 2)}^2} \sqrt{16t^2 + 4t^4 - 16t^2 + 16 + 16t^2}$

$\displaystyle ||\mathbf{T}' (t)|| = \frac{1}{{(t^2 + 2)}^2} \sqrt{4t^4 +16t^2 + 16}$

$\displaystyle ||\mathbf{T}' (t)|| = \frac{1}{{(t^2 + 2)}^2} \sqrt{4(t^4 +4t^2 + 4)}$

$\displaystyle ||\mathbf{T}' (t)|| = \frac{1}{{(t^2 + 2)}^2} \sqrt{4{(t^2 +2)}^2}$

$\displaystyle ||\mathbf{T}' (t)|| = \frac{1}{{(t^2 + 2)}^2} \cdot 2(t^2 +2)$

$\displaystyle ||\mathbf{T}' (t)|| = \frac{2}{(t^2 + 2)}$

De la fórmula de la curvatura, se sustituye lo que requiere

$\displaystyle K = \frac{|| \mathbf{T}'(t) ||}{|| \mathbf{r}'(t) ||}$

$\displaystyle K = \frac{\frac{2}{(t^2 + 2)}}{t^2 + 2}$

$\displaystyle \therefore K = \frac{2}{{(t^2 + 2)}^2}$

Problema 3. Encuentre la curvatura de la parábola dada por $\displaystyle y = x - \frac{1}{4} x^2$ en $x=2$ . Dibujar el círculo de curvatura en $(2,1)$ .