Funciones polinomiales. Cálculo diferencial.

Introducción

Las funciones pueden clasificarse, de acuerdo con su origen, en dos grandes grupos: algebraicas y trascendentales. La funciones algebraicas son aquellas cuya regla corresponde a una expresión algebraica como son funciones polinomiales, funciones racionales y funciones irracionales y las funciones transcendentales corresponden a aquellos casos en los que la función no se puede definir por sus operaciones aritméticas, de las cuales son funciones trigonométricas, funciones trigonométricas inversas, funciones exponenciales y funciones logarítmicas.

Definición

Las funciones polinomiales son todas aquellas funciones formadas por polinomios, donde el grado del polinomio lo determina el mayor exponente de la variable. Su fórmula general es:

$\displaystyle f(x) = a_n x^n + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + \cdots + a_1 x + a_0$

donde $n$ es un número positivo y $a$ es una constante real.

Función constante

Es una línea horizontal a la altura del valor de la constante. Su fórmula es $f(x) = b$ .

Un ejemplo seria $f(x) = -1.5$ (figura 1).

*Figura 1. Representando una función constante, «f(x) = -1.5».*

Función identidad

Es aquella cuya gráfica es una línea recta a 45°. La fórmula es $f(x) = x$ . Los valores del dominio son idénticos a los de la imagen.

Funcion lineal

Una función lineal ocurren cambios proporcionales de una variable respecto a otra. Esta funcion el cambio de $y$ depende tanto de su valor inicial como de la pendiente (coeficiente que acompaña a $x$ ).

Su función es de la forma $y=mx+b$ donde su dominio e imagen son todos los números reales; es decir, no tiene ninguna restricción. El signo de la pendiente $m$ representa su inclinación: positiva si va a la izquierda o negativa si va a la derecha. Para poder graficarla solo basta dos puntos y considerando lo siguiente:

a) Si la gráfica es una línea recta, se pueden asignar dos valores diferentes a $x$ y $y$ para obtener dos puntos que se unan mediante una línea recta.
b) El otro caso es intersectar la recta con los ejes.

Por ejemplo, para graficar la función $y = -5x+3$ , primero se toma $x=0$ para que la grafica se intersecte con el eje $y$ :

$\displaystyle y = -5x+3$

$\displaystyle y = -5(0) + 3$

$\displaystyle y = 3$

El punto de intersecion entre la recta y el eje $y$ es $(0,3)$ .

Ahora, si $y=0$ ,

$\displaystyle y = -5x + 3$

$\displaystyle 0 = -5x + 3$

$\displaystyle 5x = 3 \rightarrow x = \frac{3}{5}$

Por lo que el punto de interseccion entre la recta y el eje $x$ es $\displaystyle \left(\frac{3}{5},0 \right)$ .

*Figura 3. Grafica de la funcion «y=-5x+3» con los puntos de intersección calculados.*

Otro ejemplo seria una grafica de dos funciones (figura 4). La grafica linea negra representa la funcion $y=x+3$ mientras que la de la linea gris es $\displaystyle y = \frac{1}{2}x + 3$ .

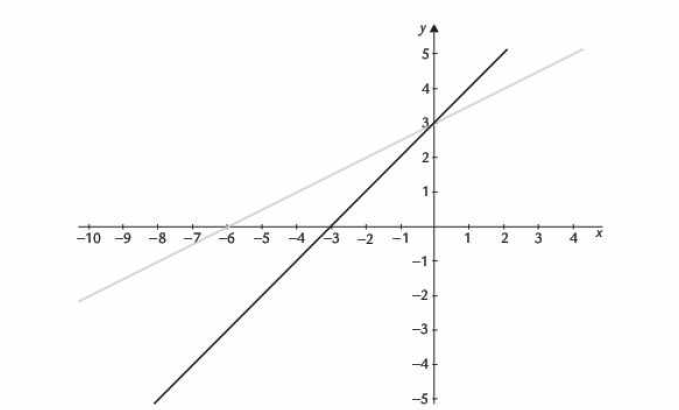
La segunda funcion se observa que la linea es mas inclinada y esto se debe a que el coeficiente de la $x$ representa una pendiente expreada de la forma

$\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1}$

Esto significa que si el resultado del denominador tiene un valor mas grande que el numerador, la grafica recorrera mas unidades de $x$ y menos de $y$ .

Función cuadrática

Es aquella de la forma $f(x) = ax^2 + bx + c$ y su dominio son todos los números reales; es decir, no hay alguna restricción. Su gráfica es una parábola donde si $a>0$ entonces será cóncava hacia arriba o si $a<0$ será cóncava hacia abajo. Su imagen está determinada por el máximo o mínimo de la función, el cual se puede obtener a partir del vértice. Además, si el coeficiente del término cuadrático es una fracción, la parábola estará más abierta; sucederá lo contrario si su coeficiente es más grande. Las intersecciones con el eje $x$ son los ceros de la ecuación, el vértice (máximo o mínimo) de la parábola está dado por el punto $(h,k)$ , donde: $\displaystyle h = - \frac{b}{2a}$ y $k = f(h)$ .

Un ejemplo para graficar una funcion esta $y = x^2 - 5x - 14$ . Comparando:

$y = x^2 - 5x - 14$ $\rightarrow$ $f(x) = ax^2 + bx + c$

donde $a=1$ , $b=-5$ y $c = -14$ .

La parábola es cóncava hacia arriba ya que $a>0$ .

Las intersecciones de la grafica con el eje x ( $y=0$ ) son

$y = x^2 - 5x - 14$

$0 = x^2 - 5x - 14$

$x^2 - 5x - 14 = 0$

(Por fórmula general)

$\displaystyle x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

$\displaystyle x = \frac{-(-5) \pm \sqrt{{(-5)}^2 - 4(1)(-14)}}{2(1)}$

$\displaystyle x = \frac{5 \pm \sqrt{25 + 56}}{2} = \frac{5 \pm \sqrt{81}}{2}$

$\displaystyle x = \frac{5 \pm 9}{2}$

$\displaystyle x_1 = 7$

$\displaystyle x_2 = -2$

Asi que, los puntos de interseccion son: $(7,0)$ y $(-2,0)$ .

Por último, el vértice se obtiene:

$\displaystyle h = - \frac{b}{2a}$

$\displaystyle h = - \frac{(-5)}{2(1)}$

$\displaystyle h = \frac{5}{2} = 2.5$

$k = f(h)$

$\displaystyle k = f \left( \frac{5}{2} \right)$

$\displaystyle k = {\left( \frac{5}{2} \right)}^2 - 5 \left( \frac{5}{2} \right) - 14 = \frac{25}{4} - \frac{25}{2} - 14$

$\displaystyle k = - \frac{81}{4} = -20.25$

Por tanto, $\displaystyle (2.5, -20.25)$

Con estos tres puntos, ya es posible graficar la funcion. El resultado se observa en la figura 5.

*Figura 5. Grafica de la funcion $y = x^2 - 5x - 14$ .*

*Figura 5. Grafica de la funcion $y = x^2 - 5x - 14$ .*

Función cúbica

Es un polinomio en el que la variable tiene un exponente de grado tres y puede estar dada por la forma $f(x) = a_3 x^3 + a_2 x^2 + a_1 x + a_0$ . Su dominio son todos los números reales ya que no tiene restricciones como divisiones o raíces; su imagen también está dada por todos los números reales. Cada coeficiente de la ecuación cúbica revela un comportamiento al momento de graficarlo. Estos puntos son:

El término $a_0$ representa el término independiente y esto hace que la gráfica puede desplazarse hacia arriba (si es $+ a_0$ ) o hacia abajo (si es $-a_0$ ) en el eje $y$
El término $a_1 x$ , conocido como término lineal, menciona qué tan grandes son las curvas
El término cuadrático $a_2 x^2$ hace desplazar la ecuación hacia la izquierda o hacia la derecha
Y el signo de la variable cúbica $a_3 x^3$ determina si tiene la forma «N» (cuando es $x^3$ , por ejemplo) o la forma «Ͷ» (cuando es $-x^3$ , por ejemplo).

Si solo existe la variable de grado tres [es decir, $f(x) = \pm x^3$ ] puede tener dos formas:

Figura 6. Hacia la derecha cuando $f(x) = x^3$

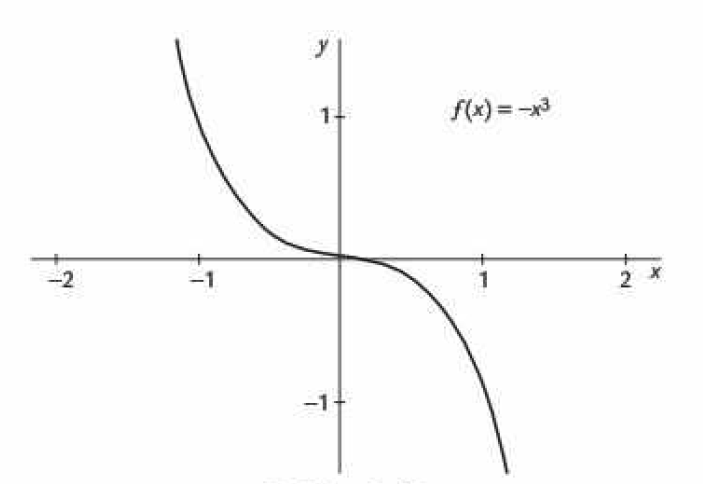
Figura 7. Hacia la izquierda cuando $f(x) = -x^3$

Si una función cúbica llega a tener más términos, tendrian la siguiente forma:

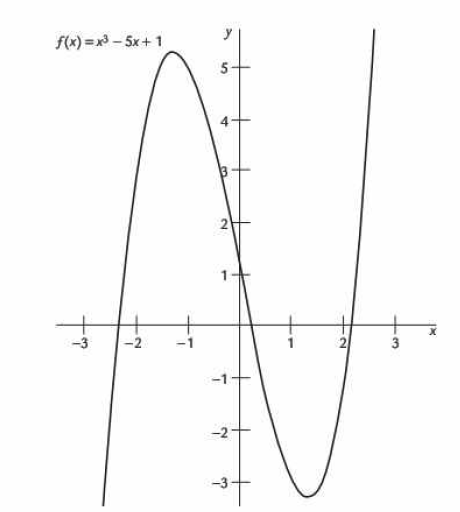
Figura 8.

Figura 9.

La manera de graficar una función cúbica es intersectarla con los ejes; se necesitan tres intersecciones con el eje $x$ , la intersección con el eje $y$ , y saber si la variable de grado tres es positiva o negativa.

Funciones polinomiales. Cálculo diferencial.

Introducción

Definición

Función constante

Función identidad

Funcion lineal

Función cuadrática

Función cúbica

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

Funciones polinomiales. Cálculo diferencial.

Introducción

Definición

Función constante

Función identidad

Funcion lineal

Función cuadrática

Función cúbica

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta