Introducción

Estos circuitos contienen sólo un único elemento de almancenamiento (capacitor o inductor) y ésa se describe mediante una ecuación diferencial de primer orden. Su ánalisis describe el comportamiento de un circuito como función del tiempo después de que ocurre un cambio súbito en la red debido a la apertura o cierre de interruptores. Debido a la presencia del elemento de almacenamiento, la respuesta del circuito a un cambio súbito atravesará por un periodo de transición antes de estabilizarse en un valor de estado estable.

Un parámetro importante en el análisis transitorio es la constante de tiempo del circuito, conocido como τ. Este parámetro revela que tan rápido respoderá el circuito a los cambios.

Forma general de las ecuaciones de respuesta

La solución general de una ecuación diferencial de primer orden

Sea

\displaystyle \frac{dx(t)}{dt} + a x(t) = f(t)

(1)

la forma general de representar una ecuación diferencial de primer orden.

Un teorema fundamental de las ecuaciones diferenciales afirma que si x(t) = x_p (t) es una solución de la ecuación (1), y x(t) = x_c (t) es una solución a una ecuación diferencial homogénea de la forma

\displaystyle \frac{dx(t)}{dt} + a x(t) = 0

(2)

Entonces

\displaystyle x(t) = x_p (t) + x_c (t)

(3)

es la solución de la ecuación (1) original. El término x_p (t) se denomina solución integral particular o respuesta forzada, mientras que x_c (t) se llama solución complementaria o respuesta natural.

Para el caso de que f(t) = A, es decir una fuente constante, la solución general de la ecuación diferencial consiste en dos partes que se obtienen resolviendo las dos ecuaciones siguientes:

\displaystyle \frac{d x_p (t)}{dt} + a x_p (t) = A

\displaystyle \frac{d x_c (t)}{dt} + a x_c (t) = 0

(4)

(5)

Resolviendo la ecuación (4) utilizando la siguiente ecuación,

\displaystyle y(x) \cdot e^{\int{P(x) \ dx}} = \int{Q(x) \cdot e^{\int{P(x) \ dx}} \ dx} + C

(6)

donde \displaystyle y(x) = x_p (t), P(x) = a, Q(x) = A, C = K_3 y dx = dt. Continuando

\displaystyle x_p (t) \cdot e^{\int{a \ dt}} = \int{A \cdot e^{\int{a \ dt}} \ dt} + K_3

\displaystyle x_p (t) \cdot e^{at} = A \int{ \cdot e^{at} \ dt} + K_3

\displaystyle x_p (t) = \frac{A}{e^{at}} \left(\frac{1}{a} e^{at} + K_3 \right) = \frac{A}{a} +\frac{K_3}{e^{at}}

\displaystyle x_p (t) = \frac{A}{a} + K_3 e^{-at}

(7)

Para la ecuación (5)

\displaystyle \frac{d x_c (t)}{dt} + a x_c (t) = 0

\displaystyle \frac{d x_c (t)}{dt} = - a x_c (t)

\displaystyle \frac{d x_c (t)}{x_c (t)} = - a dt

\displaystyle \int{\frac{d x_c (t)}{x_c (t)}} = - a \int{dt}

\displaystyle \ln{x_c (t)} = - a t + K_4

\displaystyle \ln{x_c (t)} = \ln{e^{-a t}} + \ln{K_4} = \ln{K_4 \ e^{-a t}}

\displaystyle x_c (t) = K_4 e^{-a t}

(8)

Por tanto, una solución de la ecuación (1) es

\displaystyle x(t) = x_p (t) + x_c (t)

\displaystyle x(t) = \frac{A}{a} + K_3 e^{-at} + K_4 e^{-a t}

\displaystyle x(t) = \frac{A}{a} + (K_3 + K_4) e^{-a t}

\displaystyle x(t) = \frac{A}{a} + K_2 e^{-a t}

(9)

donde la constante K_2 puede calcularse si se conoce en un instante de tiempo el valor de la variable independiente x(t).

La ecuación (9) puede expresarse en general de la forma

\displaystyle x(t) = K_1 + K_2 e^{-\frac{t}{\tau}}

(10).

donde el comportamiento de algunos los elementos de la ecuación (10) ocurren de la siguiente manera:

  • El término K_1 se denomina solución de estado estable: el valor de la variable x(t) conforme t \rightarrow \infty cuando el segundo término se hace insignificante.
  • \tau es la constante de tiempo del circuito. En la ecuación (10) se observa que el segundo término es una exponencial decreciente que tiene un valor, si \tau > 0, de K_2 para t = 0 y una valor de cero para t = \infty. La razón por la cual decrece esta exponencial es porque está determinada por el valor de esa constante de tiempo \tau.

El comportamiento de la respuesta natural

Del segundo termino de la ecuación (10)

\displaystyle x(t) = K_2 e^{-\frac{t}{\tau}}

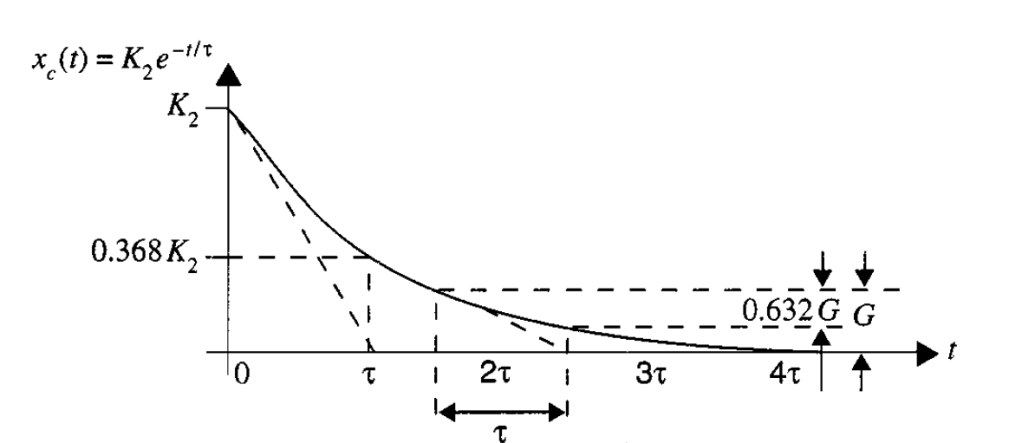
tiene la siguiente representación gráfica (figura 1). Se observa el decrecimiento de la exponencial determinada por la constante de tiempo, τ. El valor de x_c (t) ha caído de K_2 a un valor de 0.368 K_2 en una constante de tiempo, una caída del 63.2%. En dos constante de tiempo el valor de x_c (t) ha caído a 0.135K_2, una caída del 63.2% del valor al tiempo t = \tau. Esto significa que la brecha entre un punto sobre la curva y el valor final de la curva se cierra 63.2% cada constante de tiempo. Finalmente, despues de cinco constantes de tiempo, x_c (t) = 0.0067 K_2, que es menos que el 1%.

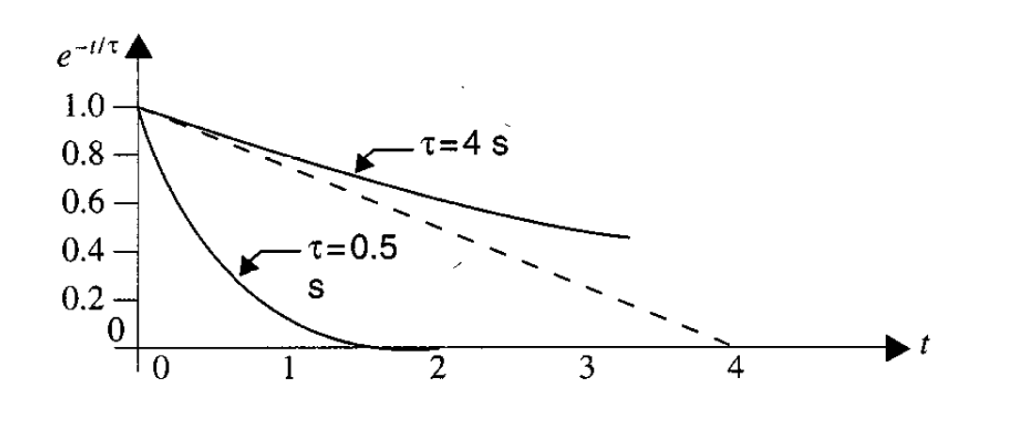
Figura 1. Representacion grafica del comportamiento de la respuesta natural ante la constante de tiempo τ.

Una propiedad interesante de la función exponencial que se observa en la figura 1 es que la pendiente inicial de la curva intersecta el eje de tiempo a un valor de t = \tau, que también se puede tomar cualquier punto sobre la curva, no solo el valor inicial, y se encuentra la constante de tiempo hallando el tiempo requerido para cerrar la brecha un 63.2%. Finalmente, la diferencia entre una constante de tiempo pequeña (es decir, respuesta rápida) y una constante de timpo grande (la cual es una respuesta más lenta) se ilustra en la figura 2. Estas curvas indican que si el circuito tiene una constante de tiempo pequeña, se restablece rapidamente a un valor de estado estable. De manera inversa, la constante de tiempo es grande, se requiere más tiempo para que el circuito se restablezca o alcance el estado estable. En cualquier caso, la respuesta del circuito escencialmente alcanza el estado estable en cinco constantes de tiempo (es decir, 5 \tau).

Figura 2. Comportamiento de la constante de tiempo τ.

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.