El caso de Fermat y la recta secante. Cálculo diferencial.

Introducción.

Este tema trata acerca de obtener una recta secante a partir de un incremento y un punto fijo arbitrario.

Además, al obtener varias rectas secantes se van aproximando a una recta tangente. Para obtener esto se utiliza la fórmula de Fermat.

Método de Fermat.

Este método lleva en nombre por Pierre de Fermat y menciona lo siguiente “la pendiente de la recta tangente de una curva es igual al límite de las pendientes de las rectas secantes cuando “h” tiende a cero”. Su fórmula es la siguiente:

$\displaystyle {m}_{tan} = \lim_{h \rightarrow 0}{{m}_{s}}$

donde ${m}_{s}$ se obtiene de:

$\displaystyle {m}_{s} = \frac{f(x) - f({x}_{0})}{x - {x}_{0}}$

Y también:

$[{x}_{0}, f({x}_{0})]$ pertenecen a las coordenadas del punto fijo

$[x , f(x)]$ pertenecen a las coordenadas del punto móvil

A partir del incremento “h” (que también algunos autores lo toman como «Δx») se despeja “{x}_{0}”:

$h = x - {x}_{0}$

$x = h + {x}_{0}$

${x}_{0} = x - h$

Problema resueltos.

Problema 1. Obtener la recta secante de la función $y = {x}^{2}$

Solución. Primero se realiza una tabulación con valores positivos y con valores negativos usando la función «y = x^2»:

Valores positivos

X	Y
0	0
1	1
2	4
3	9

Valores negativos

X	Y
0	0
-1	1
-2	4
-3	9

Arbitrariamente, se utiliza un punto fijo y para ello se puede tomar uno al azar basándose en la tabulación elaborada; por lo que utilizará la coordenada [3,9]. Esta coordenada va a representar el punto fijo:

$[{x}_{0}, f({x}_{0})] = [3, 9]$

Y claramente se observa que:

${x}_{0} = 3$

${y}_{0} = f({x}_{0}) = 9$

El valor de “h” se puede asignar arbitrariamente y será “h = 2”. Luego, despejando “x”:

$h = x - {x}_{0}$

$2 = x - 3$

$2 + 3 = x$

$5 = x$

Esto último es el valor de la abscisa del punto móvil. Para obtener su ordenada solo basta con evaluar este valor con la función del problema:

$f(x) = y = {x}^{2}$

$y = (5)^2$

$y = 25$

Por lo tanto, el punto móvil es: (5,25)

Diapositiva8 — *Figura 3.2.1. Representación gráfica referente a la ubicación del punto fijo, punto móvil y la recta secante.*

Problema 2. De lo anterior, obtener la fórmula o ecuación para tener más rectas tangentes a partir del punto fijo y desconociendo el incremento.

Solución. Recordando los datos obtenidos durante la solución del problema anterior:

$[{x}_{0}, f({x}_{0})]$

${x}_{0} = 3 \quad \quad {y}_{0} = f({x}_{0}) = 9$

Además:

$x = h + {x}_{0}$

$x = h + 3$

Sustituyendo lo anterior en la fórmula de la recta secante:

$\displaystyle {m}_{s} = \frac{f(x) - f({x}_{0})}{x - {x}_{0}} = \frac{f(x) - f(3)}{x - 3}$

$\displaystyle = \frac{f(h + 3) - f(3)}{h + 3 - 3} = \frac{f(h + 3) - f(3)}{h}$

$\displaystyle = \frac{{(h + 3)}^{2} - {(3)}^{2}}{h} = \frac{{(h+3)}^{2} - 9}{h}$

$\displaystyle = \frac{{h}^{2} + 6h + 9 - 9}{h} = \frac{{h}^{2} + 6h}{h}$

$\therefore {m}_{s} = h+ 6$

Obteniendo la recta tangente a partir de la fórmula de la recta secante (método de Fermat).

Problemas resueltos.

Problema 3. Obtener la ecuación de la recta tangente para la función

$y = {x}^{2}$

Solución. Recordando la fórmula:

$\displaystyle {m}_{tan} = \lim_{h \rightarrow 0}{{m}_{s}}$

$\displaystyle= \lim_{h \rightarrow 0}{\frac{f(x) - f({x}_{0})}{x - {x}_{0}}} = \lim_{h \rightarrow 0}{\frac{f(h + {x}_{0}) - f({x}_{0})}{h}}$

$\displaystyle = \lim_{h \rightarrow 0}{\frac{{(h + {x}_{0})}^{2} - {{x}_{0}}^{2}}{h}} = \lim_{h \rightarrow 0}{\frac{{h}^{2} + 2h{x}_{0} + {{x}_{0}}^{2} - {{x}_{0}}^{2}}{h}}$

$\displaystyle = \lim_{h \rightarrow 0}{\frac{{h}^{2} + 2h{x}_{0}}{h}} = \lim_{h \rightarrow 0}{(h + 2{x}_{0})}$

$= 0 + 2{x}_{0} = 2{x}_{0}$

$\therefore {m}_{tan} = 2{x}_{0}$

Esto último es la ecuación para obtener la pendiente de la recta tangente de la función « $y = x^2$ » para cualquier punto fijo $[x_0, f(x_0)]$ .

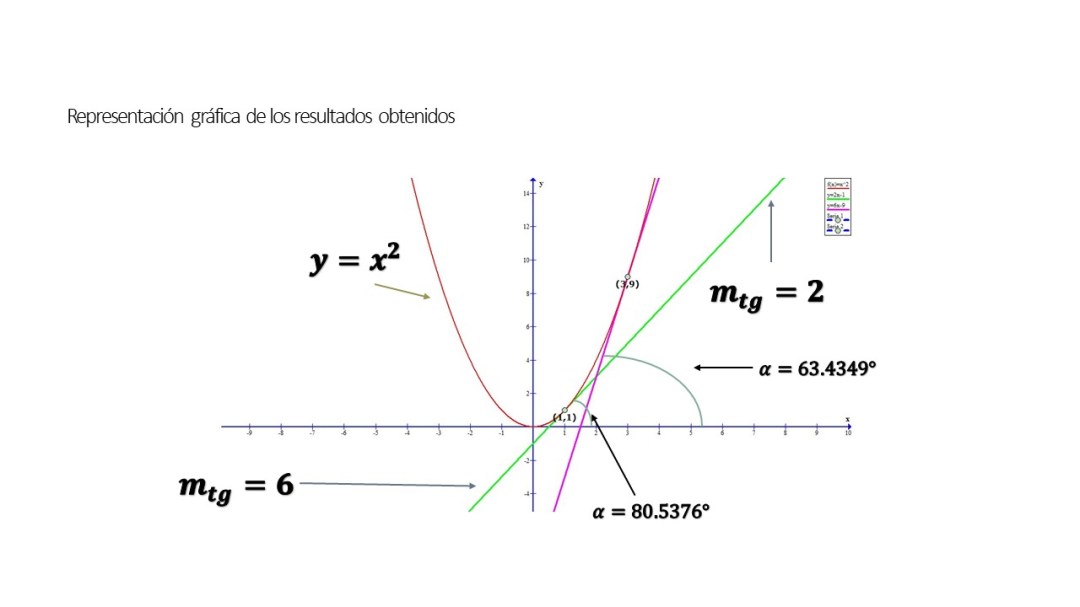
Problema 4. De la ecuación que representa la recta tangente, obtener su pendiente y ángulo respecto al eje “x” para los puntos (3, 9) y (1, 1).

Solución. Para (3, 9):

${m}_{tan} = 2{x}_{0}$

${m}_{tan} {|}_{(3,9)} = 2(3) = 6$

${m}_{tan} {|}_{(3,9)} = 6$

Y el ángulo para esta pendiente es:

${m}_{tan} = tan{\alpha}$

$tan{\alpha} = 6$

$\alpha = \arctan{(6)}$

$\therefore \alpha = 80.5376$ °

Para (1, 1):

${m}_{tan} = 2{x}_{0}$

${m}_{tan} {|}{(1,1)} = 2(1) = 2$

${m}_{tan} {|}{(1,1)} = 2$

Y el ángulo para esta pendiente es:

${m}_{tan} = tan{\alpha}$

$\tan{\alpha} = 2$

$\alpha = \arctan{(2)}$

$\alpha = 63.4349$ °

Diapositiva16 — *Figura 3.2.2. Representación gráfica de las rectas tangentes y sus respectivos ángulos.*

Referencias bibliográficas.

Aguilar Márquez, A., Bravo Vázquez, F. V., Gallegos Ruiz, H. A., Cerón Villegas, M., & Reyes Figueroa, R. (2009). Matemáticas simplificadas. México: Pearson Educación.
Gil Sevilla, J. L., & Díaz Téllez, R. (2013). Cálculo diferencial para cursos enfoque por competencias. México: Pearson Educación.
Mitacc, M., & Toro Mota, L. (2009). Tópicos de cálculo. Volumen 1. Perú: Thales S. R. L.
Swokowski, E. W. (1989). Cálculo con geometría analítica. México: Panamericana.
Thomas, J. G. (2006). Cálculo. Una variable. México: Pearson Educación.
Zill, D. G. (1999). Cálculo con geometría analítica. México.
Zill, D. G., & Wright, W. S. (2010). Matemáticas 1. Cálculo diferencial. México: Mc Graw Hill Interamericana.

El caso de Fermat y la recta secante. Cálculo diferencial.

Introducción.

Método de Fermat.

Problema resueltos.

Obteniendo la recta tangente a partir de la fórmula de la recta secante (método de Fermat).

Problemas resueltos.

Referencias bibliográficas.

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta

El caso de Fermat y la recta secante. Cálculo diferencial.

Introducción.

Método de Fermat.

Problema resueltos.

Obteniendo la recta tangente a partir de la fórmula de la recta secante (método de Fermat).

Problemas resueltos.

Referencias bibliográficas.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta