Vectores en el espacio. Cálculo vectorial.

Introducción

En el espacio los vectores se denotan mediante ternas ordenadas $\bold{v} = (v_1, v_2, v_3)$ . El vector cero se denota por $\bold{0}=(0,0,0)$ . Usando los vectores unitarios $\bold{i} = (1,0,0)$ , $\bold{j} = (0,1,0)$ y $\bold{k} = (0,0,1)$ en la dirección del eje positivo $z$ , la notación empleando los vectores unitarios canónicos o estándar para $\bold{v}$ es:

$\bold{v} = {v}_{1} \bold{i} + {v}_{2} \bold{j} + {v}_{3} \bold{k}$

Figura 1. Vectores unitarios canónicos en el espacio. Nodo Universitario de la Universidad de Guanajuato, Introducción a la geometría analítica del espacio. [Figura]. Recuperado de: https://oa.ugto.mx

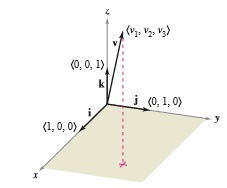
Si v se representa por el segmento de recta dirigido de $P(p_1, p_2, p_3)$ a $Q(q_1, q_2, q_3)$ , las componentes de v se obtienen restando las coordenadas del punto inicial de las coordenadas del punto final, como sigue:

$\bold{v} = ({v}_{1},{v}_{2},{v}_{3}) = ({q}{1}-{p}{1},{q}{2}-{p}{2}, {q}{3} -{p}_{3})$

Figura 2. Representando el vector v mediante el segmento de recta. Nodo Universitario de la Universidad de Guanajuato, Introducción a la geometría analítica del espacio. [Figura]. Recuperado de: https://oa.ugto.mx

Propiedades de los vectores en el espacio

Sean $\bold{u} = (u_1, u_2, u_3)$ y $\bold{v} = (v_1, v_2, v_3)$ vectores en el espacio y sea $c$ un escalar

1.- Igualdad de vectores: $\bold{u} = \bold{v}$ si y sólo si ${u}_{1} = {v}_{1}$ , ${u}_{2} = {v}_{2}$ y ${u}_{3} = {v}_{3}$ .

2.- Expresión mediante las componentes: Si $\bold{v}$ se representa por el segmento de recta dirigido de $P(p_1, p_2, p_3)$ a $Q(q_1, q_2, q_3)$ , entonces

$\bold{v} = ({v}_{1},{v}_{2},{v}_{3}) = ({q}_{1} - {p}_{1},{q}_{2}-{p}_{2}, {q}_{3} - {p}_{3})$

3.- Magnitud o longitud:

$||\bold{v}|| = \sqrt{{{v}_{1}}^{2} + {{v}_{2}}^{2} + {{v}_{3}}^{2}}$

4.- Vector unitario en la dirección de $\bold{v}$ :

$\displaystyle \bold{u} = \frac{\bold{v}}{||\bold{v}||} = \frac{1}{||\bold{v}||}({v}_{1},{v}_{2},{v}_{3})$ , donde $\bold{v} \ne 0$

5.- Suma de vectores: $\bold{v} + \bold{u} = ({v}_{1} + {u}_{1}, {v}_{2} + {u}_{2}, {v}_{3} + {u}_{3})$

6.- Multiplicación por un escalar: $c\bold{v} = (c{v}_{1}, c{v}_{2}, c{v}_{3})$

Problema resuelto

Problema. Hallar las componentes y la longitud del vector $v$ que tiene punto inicial $(-2,3,1)$ y punto final $(0,-4,4)$ . Después, hallar un vector unitario en la dirección de $\bold{v}$ .