Rectas en el espacio. Cálculo vectorial.

Introducción

En el plano se utiliza lo que es la pendiente para poder determinar una ecuación de una recta.

El segmento $\overrightarrow{PQ}$ es un múltiplo escalar de v, y se puede escribir a $\overrightarrow{PQ} = t\bold{v}$ , donde «t» representa el escalar (la cual, es un número real).

$\overrightarrow{PQ} = (x - {x}_{1}, y - {y}_{1}, z - {z}_{1})$

$\overrightarrow{PQ} = (at, bt, ct) = t\bold{v}$

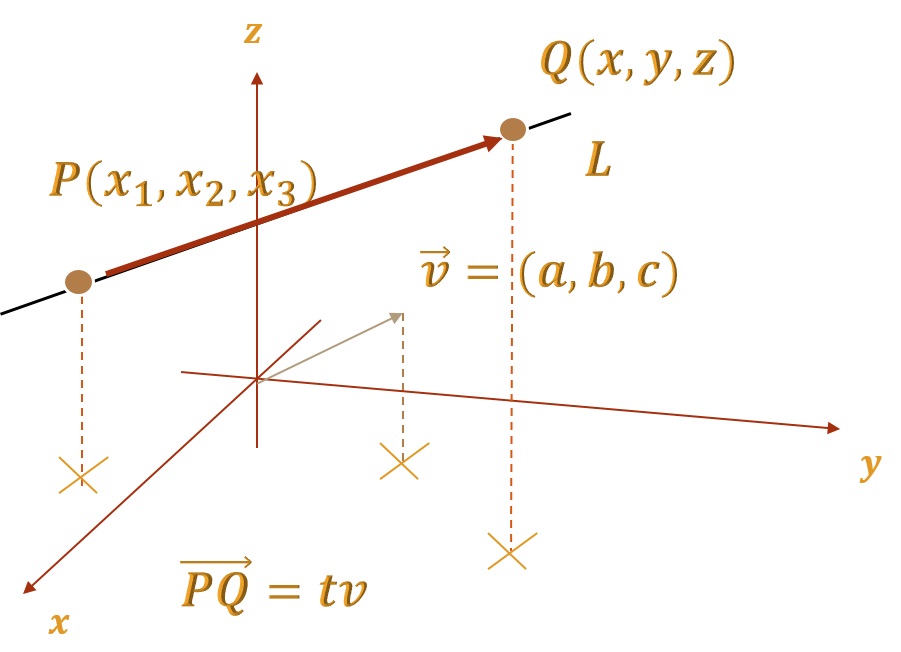
Imagen1 — *Figura 1.8.1 Representación gráfica de una recta en el espacio.*

Ahora, una recta L paralela al vector $\bold{v} = (a, b, c)$ y que pasa por el punto $P({x}_{1}, {y}_{1}, {z}_{1})$ se representa por medio de ecuaciones paramétricas

$x = {x}_{1} + at$

$y = {y}_{1} + bt$

$z = {z}_{1} + ct$

Y la siguiente expresión representa una ecuación simétrica

$\displaystyle \frac{x - {x}_{1}}{a} = \frac{y - {y}_{1}}{b} = \frac{z - {z}_{1}}{c}$

Problemas resueltos

Problema 1. Hallar las ecuaciones paramétricas y simétricas de la recta L que pasa por el punto (1,-2,4) y es paralela a v = (2,4,-4).

Solución. De acuerdo con el punto

$P({x}_{1}, {y}_{1}, {z}_{1}) = P(1, -2, 4)$

Y con el vector

$\bold{v} = (a, b, c) = (2, 4, -4)$

Se va obteniendo las ecuaciones paramétricas

$x = {x}_{1} + at \quad \rightarrow \quad \therefore x = 1 + 2t$

$y = {y}_{1} + bt \quad \rightarrow \quad \therefore y = -2 + 4t$

$z = {z}_{1} + ct \quad \rightarrow \quad \therefore z = 4 - 4t$

Por lo que las ecuaciones simétricas son

$\displaystyle \frac{x - {x}_{1}}{a} = \frac{y - {y}_{1}}{b} = \frac{z - {z}_{1}}{c}$

$\displaystyle \therefore \frac{x - 1}{2} = \frac{y + 2}{4} = - \frac{z - 4}{4}$

Problema 2. Hallar un conjunto de ecuaciones paramétricas de la recta que pasa por los puntos (-2,1,0) y (1,3,5).

Solución. De acuerdo con lo siguiente

$\bold{v} = \overrightarrow{PQ} = [1 - (-2), 3 - 1, 5 - 0] = (3, 2, 5) = (a, b, c)$

Donde «a = 3», «b = 2» y «c = 5».

Y mediante estos datos y con el punto inicial que es ${P}_{1} (-2, 1, 0)$ ya se obtienen las ecuaciones paramétricas:

$x = {x}_{1} + at \quad \rightarrow \quad \therefore x = -2 + 3t$

$y = {y}_{1} + bt \quad \rightarrow \quad \therefore y = 1 + 2t$

$z = {z}_{1} + ct \quad \rightarrow \quad \therefore z=5t$

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web. Ver todas las entradas de Cesar Reyes

Deja un comentario Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.