Planos en el espacio. Cálculo vectorial.

Introducción

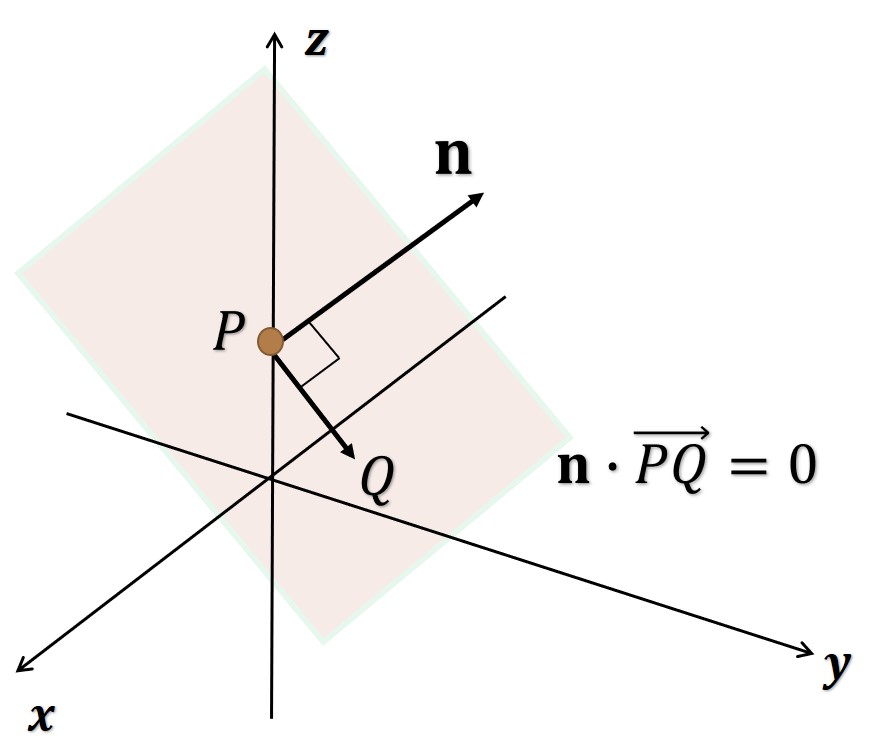
Una ecuación de un plano en el espacio se puede obtener a partir de un punto en el plano y de un vector normal (perpendicular) al plano. En el plano contiene un punto $P({x}_{1}, {y}_{1}, {z}_{1})$ y presenta un vector normal diferente de cero $\bold{n} = (a, b, c)$ . En este plano muestra todos los puntos Q(x,y,z) para que el vector $\overrightarrow{PQ}$ es ortogonal a $\bold{n}$ . Por lo tanto, la ecuación canónica o estándar de un plano en el espacio es la siguiente

$\bold{n} \cdot \overrightarrow{PQ} = 0$

$(a,b,c) \cdot (x-x_1, y-y_1, z-z_1) = 0$

$a(x - {x}_{1}) + b(y - {y}_{1}) + c(z - {z}_{1}) = 0$

Y su forma general de la ecuación de un plano en el espacio es

$ax + by + cz + d = 0$

Figura 1. Representación gráfica del vector normal a todo vector PQ en el plano.

Problema resuelto

Problema. Hallar la ecuación general que contiene los puntos (2,1,1), (0,4,1) y (-2,1,4).

Solución. Primero calcula el vector u en los puntos (2,1,1) y (0,4,1)

$\bold{u} = (0-2, 4-1, 1-1) = (-2, 3, 0)$

Luego se calcula el vector v por medio de los puntos (0,4,1) y (-2,1,4)

$\bold{v} = (-2-0, 1-4, 4-1) = (-2, -3, 3)$

Ahora, se resuelve por producto cruz para encontrar el vector normal utilizando los vectores anteriores (es decir, u y v)

$\bold{n} = \bold{u} \times \bold{v} = \left[ \begin{matrix} \bold{i} & \bold{j} & \bold{k} \\ -2 & 3 & 0 \\ -2 & -3 & 3 \end{matrix} \right]$

$\bold{n} = (9\bold{i} + 0\bold{j} +6\bold{k}) - (-6\bold{k} + 0\bold{i} - 6\bold{j})$

$\therefore \bold{n} = 9\bold{i}+ 6\bold{j} + 12\bold{k} = (9, 6, 12)$

Finalmente, encontrando la ecuación general, primero, su expresión será una ecuación canónica teniendo el vector normal y el primer punto [es decir, (2,1,1)]

$a(x - {x}_{1}) + b(y - {y}_{1}) + c(z - {z}_{1}) = 0$

$9(x - 2) + 6(y - 1) + 12(z - 1) = 0$

Finalmente

$9(x - 2) + 6(y - 1) + 12(z - 1) = 0$

$9x - 18 + 6y - 6 + 12z - 12 = 0$

$9x + 6y + 12z - 36 = 0$

$3x + 2y + 4z - 9 = 0$

La ecuación general es

$\therefore 3x + 2y + 4z - 9 = 0$

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web. Ver todas las entradas de Cesar Reyes

Deja un comentario Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.