Punto de corte. Aplicaciones de cálculo diferencial.

Problema 1. Hallar el punto en que la línea tangente que traza a la curva $y=x^3 - 2$ en el (2,6), corta nuevamente la curva.

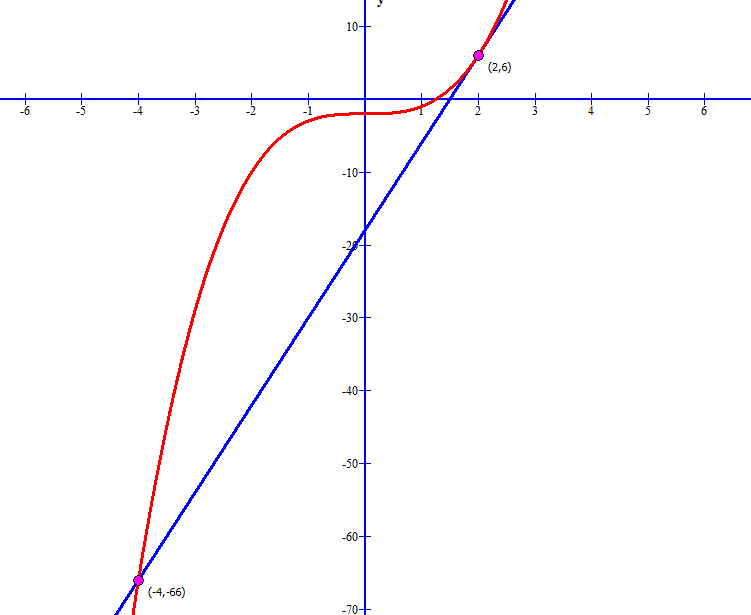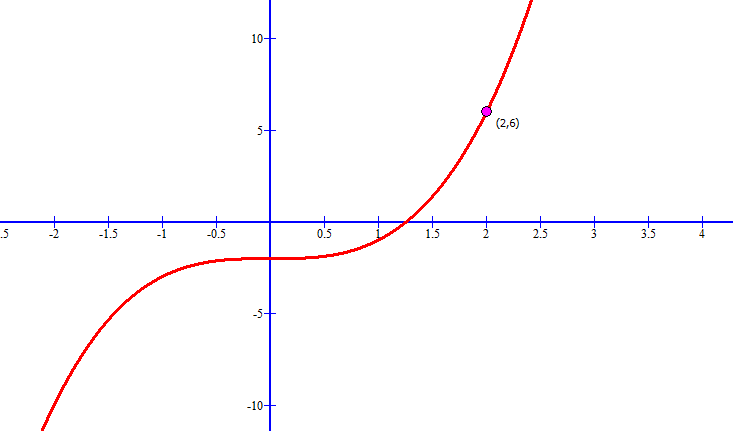
Imagen1 — *Figura 1.1.1 Representación gráfica del problema 1.*

Solución. Se deriva la función con respecto a la variable independiente, es decir con respecto a “x”.

$y={x}^{3} - 2$

$\displaystyle \frac{dy}{dx} = \frac{d}{dx} \left({x}^{3} - 2 \right)$

$\displaystyle \frac{dy}{dx} = \frac{d}{dx} ({x}^{3} ) - \frac{d}{dx} (2)$

$\displaystyle \frac{dy}{dx} = 3{x}^{2} - 0$

$\displaystyle \frac{dy}{dx} = 3{x}^{2}$

Después, se calcula el valor de la derivada usando el punto (2,6).

$\displaystyle \frac{dy}{dx}{|}_{P(2,6)} = 3{(2)}^{2}=3(4)=12$

$\displaystyle {m}_{tan} = \frac{dy}{dx}{|}_{P(2,6)} =12$

Este valor representa la pendiente de la línea tangente. Para conocer el ángulo de inclinación de la recta con respecto al eje x:

$\displaystyle {m}_{tan} = 12$

$\displaystyle \tan {\alpha}= 12$

$\displaystyle \alpha = \arctan{(12)} = {\tan}^{-1}{(12)}$

$\displaystyle \therefore \alpha =85.24$ °

Imagen2 — *Figura 1.1.2 Representación de la recta tangente.*

Por geometría analítica, se utiliza la ecuación de punto y pendiente para obtener la línea recta.

$\displaystyle {m}_{tan}=\frac{y-{y}_{0}}{x - {x}_{0}}$

$\displaystyle 12=\frac{y - 6}{x - 2}$

Se despeja la variables “y”.

$\displaystyle 12 = \frac{y - 6}{x - 2}$

$\displaystyle \frac{y - 6}{x - 2}=12$

$y - 6=12(x - 2)$

$y - 6=12x - 24$

$y=6+12x-24$

$y=12x-18$

Finalmente, se obtiene el punto de corte al igualar las ecuaciones y reduciendo términos semejantes.

$y={x}^{3} - 2$

$12x - 18 = {x}^{3} - 2$

${x}^{3} - 2 - 12x + 18 = 0$

${x}^{3} - 12x + 16 = 0$

Para encontrar las raíces de esa ecuación se utiliza el método de Ruffini:

Imagen3 — *Tabla 1.1.1 Procedimiento del método de Ruffinni.*

El valor que se utilizó en este método es “x = – 4”. Entonces:

${x}^{3} - 12x + 16 = 0$

$(x+4)({x}^{2} - 4x + 4) = 0$

Factorizando el término cuadrático:

$(x+4)({x}^{2} - 4x + 4) = 0$

$(x+4)(x - 2)(x - 2)=0$

Al evaluar las tres raíces, se observa que:

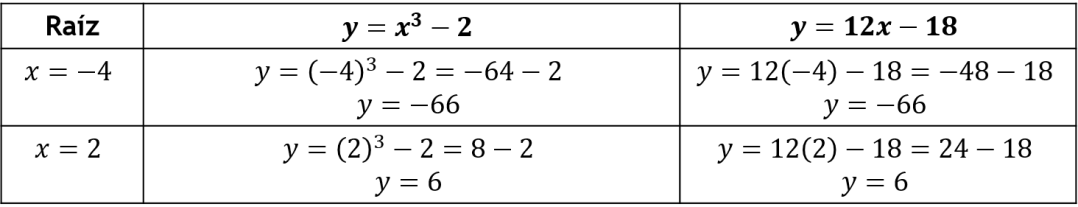
Imagen4 — *Tabla 1.1.2 Evaluación de las funciones dadas por el problema utilizando los valores de «x» obtenidos.*

Por lo que, en la raíz “x = – 4” es el segundo punto de corte. Por lo tanto, se dice que la recta tangente a la curva vuelve a cortar en el punto:

$\therefore (x, y) = (-4, -66)$

Imagen5 — *Figura 1.1.3 Representación gráfica del siguiente punto.*

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web. Ver todas las entradas de Cesar Reyes

Deja un comentario Cancelar la respuesta

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.

Punto de corte. Aplicaciones de cálculo diferencial.

Comparte esto:

Relacionado

Publicado por Cesar Reyes

Deja un comentario Cancelar la respuesta