Problema 2. El cable de suspensión de un puente colgante está anclado a dos pilares de soporte separados entre sí 100 m. El cable que está colgado tiene forma de una parábola con un punto más a bajo a 20 m bajo los puntos de suspensión. Encontrar el ángulo formado por el cable y uno de los pilares.

Solución. Por geometría analítica, se sabe que la ecuación de la parábola pasa por el origen (0,0) y el eje vertical es:

y=b{x}^{2}

Donde “b” es una constante.

El cable colgado tiene una distancia de 100 (m) entre pilar y pilar y una altura de 20 (m) de cada pilar, por gráficas se encuentran los puntos:

(- 50, 20) \quad y \quad (50, 20)

Por lo que al tomar el segundo punto (50, 20), se obtiene el valor de “b”.

y=b{x}^{2}

20=b{(50)}^{2}

\displaystyle b=\frac{20}{{(50)}^{2}} = \frac{20}{2500} = \frac{1}{125}

La función es:

y=b{x}^{2}

\displaystyle y=\frac{1}{125}{x}^{2}

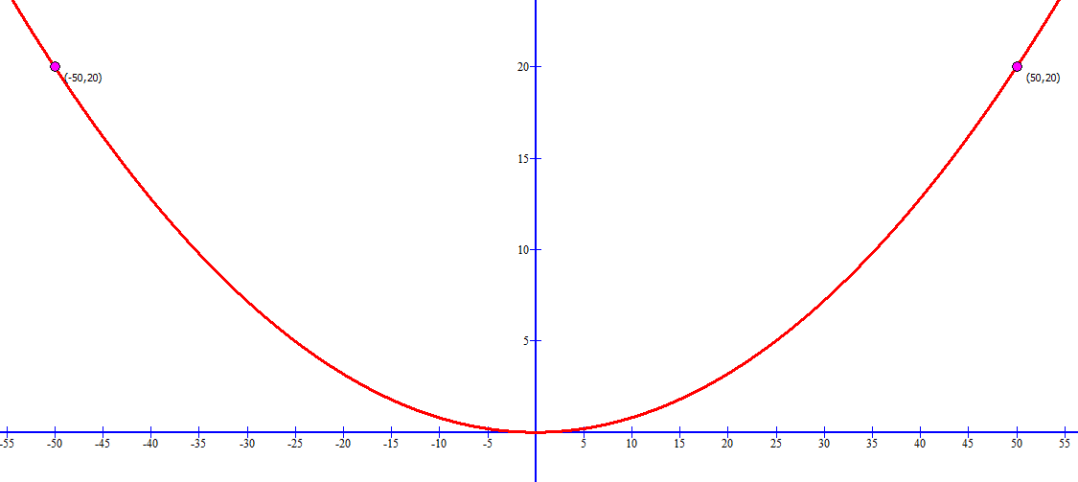
Imagen6
Figura 1.2.1 Representación gráfica del cable

A partir de esta función se obtiene su derivada con respecto a “x”:

\displaystyle y=\frac{1}{125} {x}^{2}

\displaystyle \frac{dy}{dx} = \frac{d}{dx} (\frac{1}{125} {x}^{2})

\displaystyle \frac{dy}{dx}=\left(\frac{1}{125}\right) \frac{d}{dx}{({x}^{2})}

\displaystyle \frac{dy}{dx} = \frac{1}{125} (2x)

\displaystyle \frac{dy}{dx} = \frac{2}{125} x

Usando nuevamente el segundo punto (50, 20), se encuentra la pendiente:

\displaystyle \frac{dy}{dx} = \frac{2}{125}x

\displaystyle \frac{dy}{dx} {|}_{P(50,20)} = \frac{2}{125}(50) = \frac{100}{125} = 0.8

{m}_{tan} = 0.8

\tan {\alpha} = 0.8

\alpha = \arctan{(0.8)} = 38.66°

Este ángulo mide desde el eje horizontal hasta la pendiente.

Imagen7
Figura 1.2.2 Representación gráfica de la pendiente.

Analizando esto como un triángulo rectángulo:

Imagen8
Figura 1.2.3 Representación trigonométrica de la recta tangente, el cable y el pilar.

Para obtener el ángulo entre el pilar y el cable (la parábola), se hace lo siguiente:

90 + \alpha + \beta = 180

Observando de que se trata de un triangulo rectángulo.

Despejando “β”:

\beta = 180 - 90 - \alpha

\beta = 90 - \alpha

Sustituyendo:

\beta = 90 - 38.66

\therefore \beta = 51.34°

Por lo tanto, entre el cable y el pilar forman un ángulo de 51.34°.

Avatar de Desconocido

Publicado por Cesar Reyes

Dedicado a compartir información temas referentes al cálculo básicos, intermedios y avanzados mediante presentaciones PDF, videos y publicaciones en este sitio web.

Deja un comentario

Este sitio utiliza Akismet para reducir el spam. Conoce cómo se procesan los datos de tus comentarios.