El avión y el cohete. Aplicaciones de cálculo diferencial.

Problema 4. Un avión sigue una trayectoria

$\displaystyle y = \frac{{2}^{x}}{\ln{2}}$

Se dispara contra él un cohete interceptor que sigue una trayectoria $y = x^2 + x$ en su rama del primer cuadrante. Calcular:

a) Los valores de “x” posibles cuando el avión y el cohete lleven la misma dirección.

b) El valor del ángulo cuando los dos objetos lleven la misma dirección.

Imagen17 — *Figura 1.4.1 Trayectoria del avión.*

Imagen18 — *Figura 1.4.2 Trayectoria del cohete.*

Imagen19 — *Figura 1.4.3 Trayectoria del avión y del cohete.*

Solución. Derivando la función del avión:

$\displaystyle y = \frac{{2}^{x}}{\ln{2}}$

$\displaystyle \frac{dy}{dx} = \frac{d}{dx} (\frac{2^x}{\ln{2}}) = \frac{1}{\ln{2}} \frac{d}{dx} ({2}^{x}) = \frac{1}{\ln{2}} ({2}^{x} \ln{2})$

$\displaystyle \frac{dy}{dx} = {2}^{x}$

Derivando la función del cohete:

$y = x^2 + x$

$\displaystyle \frac{dy}{dx} = \frac{d}{dx} (x^2+x) = \frac{d}{dx} (x^2) + \frac{d}{dx} (x)$

$\displaystyle \frac{dy}{dx} = 2x + 1$

Del a), el avión y el cohete irán en la misma dirección cuando sus derivadas sean iguales. Es decir:

$De \quad \frac{dy}{dx} = {2}^{x} \quad y \quad \frac{dy}{dx} = 2x + 1$

${2}^{x} = 2x + 1$

Después, se necesita encontrar los valores de “x” para que esas derivadas sean iguales. Por lo tanto, se utilizará el método de Newton – Raphson, donde igualando a cero la expresión anterior:

${2}^{x} = 2x + 1$

${2}^{x} - 2x - 1 = 0$

La nueva “y” será la siguiente:

$y = {2}^{x} - 2x - 1$

Con una tolerancia de 0.001.

Por medio de una tabulación, se analiza si en los resultados de la función presenta cambios de signo (raíz) tomando solo valores positivos en el dominio a partir del 0.

Imagen20

Tabla 1.4.1 Tabulación de la nueva función tomando valores positivos de «x».

Existen dos cambios de signo: entre 0 y 1 y entre 2 y 3.

Comenzando en el primer cambio de signo (entre 0 y 1), se usa la siguiente fórmula:

$\displaystyle {x}_{0} = \frac{(b+a)}{2}$

$\displaystyle {x}_{0} = \frac{1+0}{2} = \frac{1}{2} = 0.5$

Y con esto, se obtiene el primer punto de iteración. Luego, derivando la nueva función con respecto a “x”:

$y = {2}^{x} - 2x - 1$

$f(x) = {2}^{x} - 2x - 1$

${f}^{'} (x) = {2}^{x} \ln{2} - 2$

Sustituyendo en la fórmula del método de Newton – Raphson:

$\displaystyle {x}_{1} = {x}_{0} - \frac{f({x}_{0})}{{f}^{'} ({x}_{0})} = 0.5 - \frac{f(0.5)}{{f}^{'} (0.5)}$

$\displaystyle {x}_{1} = 0.5 - \left[ \frac{{2}^{0.5} - 2(0.5) - 1}{{2}^{0.5} \ln{2} - 2} \right] = 0.5 - \left(\frac{-0.586}{-1.02} \right) = 0.5 - 0.575$

${x}_{1} = -0.075$

Utilizando la fórmula del error:

${E}_{1} = |{x}_{1} - {x}_{0}|$

${E}_{1} = |- 0.075 - 0.5| = |- 0.575|$

${E}_{1} = 0.575$

${E}_{1} > 0.001$

Como este error es mayor que la tolerancia, se sigue el procedimiento hasta que el error sea menor o igual que 0.001. Con ${x}_{1}=-0.075$ :

$\displaystyle {x}_{2} = {x}_{1} - \frac{f({x}_{1})}{{f}^{'} ({x}_{1})}$

$\displaystyle = - 0.075 - \frac{f(- 0.075)}{{f}^{'}(- 0.075)} = - 0.075 - \left[ \frac{{2}^{(-0.075)} - 2(- 0.075) - 1}{{2}^{(-0.075)} \ln{2} - 2} \right]$

$= - 0.075 - (- 0.074) = - 0.075 + 0.074$

${x}_{2} = - 0.001$

Utilizando la fórmula del error:

${E}_{2} = |{x}_{2} - {x}_{1}|$

${E}_{2} = |- 0.001 + 0.075| = |+ 0.074|$

${E}_{2} = 0.074$

${E}_{2} > 0.001$

Con ${x}_{2}=-0.001$ :

$\displaystyle {x}_{3} = {x}_{2} - \frac{f({x}_{2})}{{f}^{'} ({x}_{2})}$

$\displaystyle = - 0.001 - \frac{f(-0.001)}{{f}^{'} (-0.001)} = - 0.001 -\left[ \frac{{2}^{(-0.001)} - 2(-0.001) - 1}{{2}^{(-0.001)} \ln{2} - 2} \right]$

$= -0.001 - (-0.001) = -0.001 + 0.001$

${x}_{3} = 0$

Utilizando la fórmula del error:

${E}_{3} = |{x}_{3} - {x}_{2}|$

${E}_{3} = |0 + 0.001| = |0.001|$

${E}_{3} = 0.001$

El error ya es igual a la tolerancia, por lo que, el valor de x a tomar es “ $x = {x}_{3} = 0$ ”.

Ahora, estudiando el segundo cambio de signo (entre 2 y 3), se usa la siguiente fórmula:

$\displaystyle {x}_{0} = \frac{(b+a)}{2}$

$\displaystyle {x}_{0} = \frac{3+2}{2} = \frac{5}{2} = 2.5$

Y con esto, se obtiene el primer punto de iteración. Se seguirán utilizando la nueva función de “y” y su derivada obtenidos en el análisis del primer cambio de signo.

Sustituyendo en la fórmula del método de Newton – Raphson:

$\displaystyle {x}_{1} = {x}_{0} - \frac{f({x}_{0})}{{f}^{'} ({x}_{0})}$

$\displaystyle {x}_{1} = 2.5 - \frac{f(2.5)}{{f}^{'} (2.5)} = 2.5 - \left[ \frac{{2}^{2.5} - 2(2.5) - 1}{{2}^{2.5} \ln{2} - 2} \right]$

$\displaystyle {x}_{1} = 2.5 - \left( \frac{-0.343}{1.921} \right) = 2.5 - (-0.179)$

${x}_{1} = 2.679$

Utilizando la fórmula del error:

${E}_{1} = |{x}_{1} - {x}_{0}|$

${E}_{1} = |2.679 - 2.5| = |0.179|$

${E}_{1} = 0.179$

${E}_{1} > 0.001$

Como este error es mayor que la tolerancia, se sigue el procedimiento hasta que el error sea menor o igual que 0.001. Con ${x}_{1} = 2.679$ :

$\displaystyle {x}_{2} = {x}_{1} - \frac{f({x}_{1})}{{f}^{'} ({x}_{1})}$

$\displaystyle {x}_{2} = 2.679 - \frac{f(2.679)}{{f}^{'} (2.679)} = 2.679 - \left[ \frac{{2}^{2.679} - 2(2.679) - 1}{{2}^{2.679} \ln{2} - 2} \right]$

$\displaystyle {x}_{2} = 2.679 - \left( \frac{0.046}{2.439} \right) = 2.679 - 0.019$

${x}_{2} = 2.66$

Utilizando la fórmula del error:

${E}_{2} = |{x}_{2} - {x}_{1}|$

${E}_{2} = |2.66 - 2.679| = |-0.019|$

${E}_{2} = 0.019$

${E}_{2} > 0.001$

Con ${x}_{2} = 2.66$ :

$\displaystyle {x}_{3} = {x}_{2} - \frac{f ({x}_{2})}{{f}^{'} ({x}_{2})}$

$\displaystyle {x}_{3} = 2.66 - \frac{f(2.66)}{{f}^{'} (2.66)} = 2.66 - \left[\frac{{2}^{2.66} - 2(2.66) - 1}{{2}^{2.66} \ln{2} - 2} \right] = 2.66 - 0$

${x}_{3} = 2.66$

Utilizando la fórmula del error:

${E}_{3} = |{x}_{3} - {x}_{2}|$

${E}_{3} = |2.66 - 2.66| = |0|$

${E}_{3} = 0$

${E}_{3} < 0.001$

El error ya es menor que la tolerancia, por lo que, el valor de x a tomar es “ $x = {x}_{3} = 2.66$ ”.

Así que, las direcciones serán iguales cuando x = 0 y x = 2.66. Esto se comprueba graficando las derivadas.

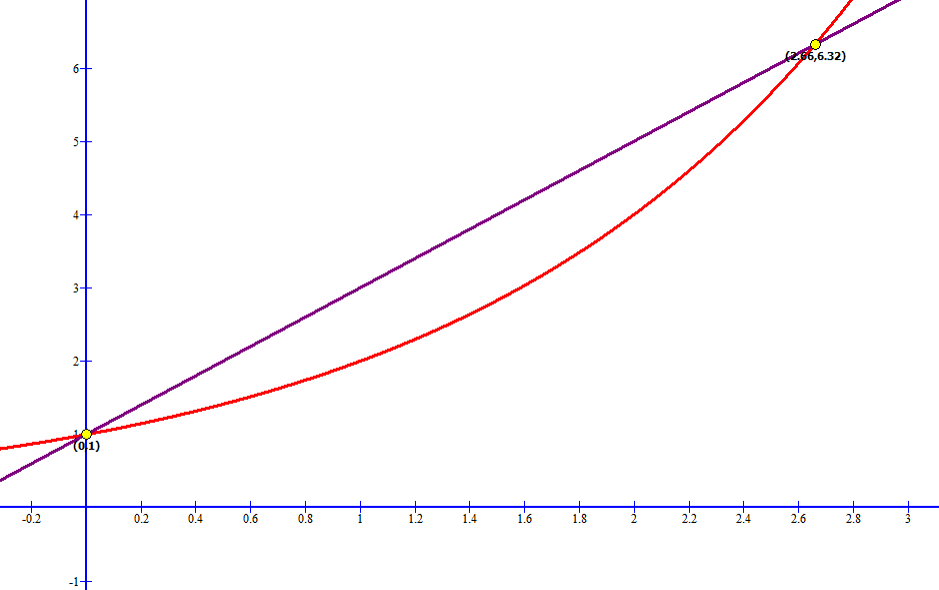
Imagen21 — *Figura 1.4.4 Comprobación de los resultados finales obtenidos por el método de Newton – Raphson.*

Del b), para obtener el ángulo en esos puntos, se puede utilizar cualquiera de las dos derivadas. Por comodidad se utilizará $\frac{dy}{dx} = 2x + 1$ . Cuando x = 0, la dirección es: